Đ s 7ề ố
Đ THI H C KÌ 1 – Năm h c 2010 – 2011Ề Ọ ọ
Môn TOÁN L p 11ớ
Th i gian làm bài 90 phútờ
I. PH N CHUNG (7 đi m)Ầ ể
Câu 1: (2 đi m)ể
1) Gi i các ph ng trình l ng giác sau :ả ươ ượ
a) (0,5đ)
x3
sin 3 2
π
� �
− =
� �
� �
b) (0,5đ)
x x
2
5cos 6cos 1 0+ + =
c) (0,5đ)
x x xcos cos3 cos5 0− + =
2) (0,5đ) Tìm giá tr l n nh t, nh nh t c a hàm s ị ớ ấ ỏ ấ ủ ố
y x xcos2 3sin2= −
Câu 2: (3 đi m) M t t h c sinh có 15 b n trong đó có 4 b n gi i Toán, 5 b n gi i Lý , 6 b n gi iể ộ ổ ọ ạ ạ ỏ ạ ỏ ạ ỏ
Hóa. Giáo viên mu n ch n ba b n h c sinh tham d cu c thi đ vui. ố ọ ạ ọ ự ộ ố
1) (1đ) H i giáo viên có bao nhiêu cách ch n ? ỏ ọ
2) (1đ) Tính xác su t đ giáo viên ch n đ c ba b n cùng môn ? ấ ể ọ ượ ạ
3) (1đ) Tính xác su t đ giáo viên ch n đ c ít nh t m t b n gi i toán ? ấ ể ọ ượ ấ ộ ạ ỏ
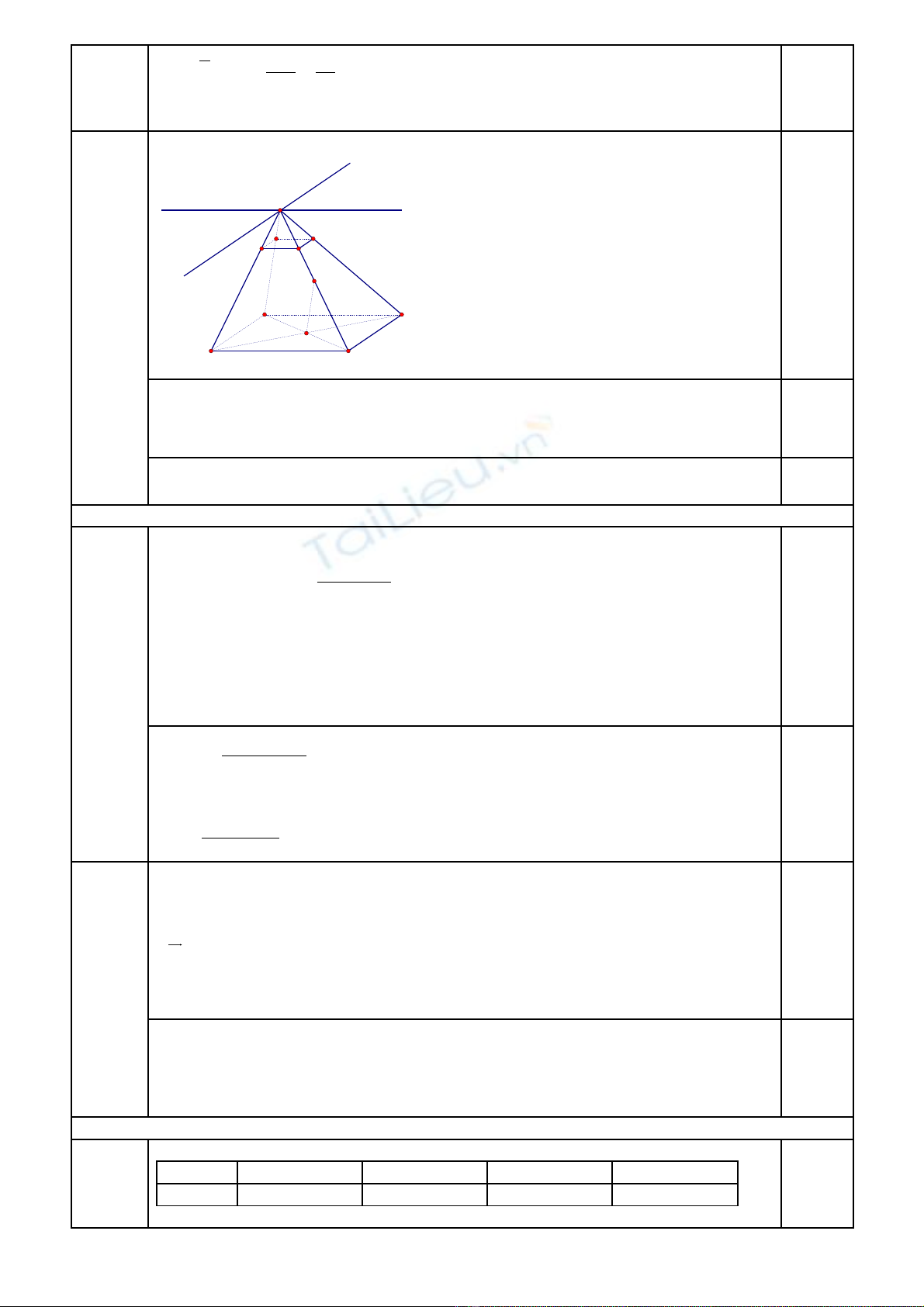
Câu 3: (2 đi m) Cho hình chóp S.ABCD có đáy ABCD là m t hình bình hành.ể ộ
1) (0,75đ) Xác đ nh giao tuy n c a (SAB) và (SCD), (SAD) và (SBC).ị ế ủ
2) (0,5đ) M t m t ph ng ộ ặ ẳ
( )
α
c t các c nh SA, SB, SC, SD l n l t t i A’, B’, C’, D’sao cho Aắ ạ ầ ượ ạ
khác A’ và t giác A’B’C’D’ cũng là hình bình hành. Ch ng minh r ng m t ph ngứ ứ ằ ặ ẳ
( )
α
song song
v i m t ph ng (ABCD). ớ ặ ẳ
3) (0,75đ) G i O là giao đi m hai đ ng chéo AC và BD. I là trung đi m c a SC. Ch ng minh OIọ ể ườ ể ủ ứ
song song v i m t ph ng (SAB). ớ ặ ẳ
II. PH N RIÊNGẦ
A. Theo ch ng trình chu n ươ ẩ
Câu 4a: (1,5 đi m)ể
a) (0,75đ) Tính s h ng đ u uố ạ ầ 1 và công sai d c a c p s c ng (uủ ấ ố ộ n) bi t : ế
u u
S
1 5
4
2 0
14
+ =
=
b) ( 0,75đ) Tính t ng 10 s h ng đ u c a c p s c ng trên. ổ ố ạ ầ ủ ấ ố ộ
Câu 5a: (1,5 đi m) Trong m t ph ng v i h tr c t a đ Oể ặ ẳ ớ ệ ụ ọ ộ xy, cho hai đi m A(–3; 1), B(0; –2) vàể
đ ng th ng d có ph ng trình: 2ườ ẳ ươ x + 3y = 6 .
a) (1đ) Tìm t a đ c a vect ọ ộ ủ ơ
AB
uuur
và tìm nh c a đ ng th ng d qua phép t nh ti n theo vect ả ủ ườ ẳ ị ế ơ
AB
uuur
.
b) (0,5đ) Tìm nh c a các đi m A, B qua phép đ i x ng tâm I (–1; –2). ả ủ ể ố ứ
B. Theo ch ng trình nâng cao ươ
Câu 4b: (1,5 đi m) Xác su t b n trúng tâm c a An là 0,4. An b n ba l n. G i X là s l n b n trúngể ấ ắ ủ ắ ầ ọ ố ầ ắ
tâm c a An. ủ
a) (1đ) L p b ng phân b xác su t c a X.ậ ả ố ấ ủ
b) (0,5đ) Tính E(X), V(X).
Câu 5b: Trong m t ph ng v i h tr c t a đ Oặ ẳ ớ ệ ụ ọ ộ xy, cho hai đi m A(–3; 1) ,B(0; –2) và đ ng th ng dể ườ ẳ
có ph ng trình: 2ươ x + 3y = 6.
a) (1đ) Tìm t a đ c a véct ọ ộ ủ ơ
AB
uuur
và tìm nh c a đ ng th ng d qua phép t nh ti n theo véct ả ủ ườ ẳ ị ế ơ
AB
uuur
.
b) (0,5đ) Tìm nh c a các đi m A, B qua phép đ i x ng tâm I (–1; –2). ả ủ ể ố ứ
––––––––––––––––––––H t–––––––––––––––––––ế
H và tên thí sinhọ: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SBD :. . . . . . . . . .
1
Đ s 7ề ố
Đ THI H C KÌ 1 – Năm h c 2010 – 2011Ề Ọ ọ
Môn TOÁN L p 11ớ
Th i gian làm bài 90 phútờ
Câu N i dungộĐi mể
1.1
a)
x3
sin 3 2
π
� �
− =
� �
� �
x k
x k
2
3 3
22
3 3
π π π
π π π
−=+
− = +
x k
x k
22
32
ππ
π π
= +
= +
Vây ph ng trình có nghi m ươ ệ
x k
x k
22
32
ππ
π π
= +
= +
(k
Z)
0,25
0,25
b)
x x
2
5cos 6cos 1 0+ + =
Đ t t = cosặx (đk :
t1
)
Ta có :
t t
2
5 6 1 0+ + =
t
t
1
1
5
= −
−
=
V i t = –1 ớ
cosx = –1
x k2
π π
= +
(k
Z)
V i t = ớ
1
5
−
cosx =
1
5
−
x = arccos(
1
5
−
) + k2
π
(k
Z)
0,25
0,25
c)
x x xcos cos3 cos5 0− + =
x x xcos cos5 cos3 0+ − =
x x x2cos3 cos2 cos3 0
− =
x xcos3 (2cos2 1) 0− =
x
x
cos3 0
2cos2 1 0
=
− =
x k
x
321
cos2 2
ππ
= +
=
k
x
x k
x k
6 3
6
6
π π
ππ
ππ
= +
= +
= − +
(k
Z)
0,25
0,25
1.2
y x xcos2 3sin2= −
= 2
x x
1 3
cos2 sin2
2 2
� �
−
� �
� �
= 2
xsin 2
3
π
� �
−
� �
� �
Ta có:
x1 sin 2 1
3
π
� �
− −
� �
� �
x2 2sin 2 2
3
π
� �
− −
� �
� �
V y GTLN là 2 ; GTNN là –2ậ
0,25
0,25
2a) S cách ch n ba b n trong 15 b n là t h p ch p 2 c a 15 ố ọ ạ ạ ổ ợ ậ ủ
n C3
15
( ) 455
Ω
= =
cách ch n ọ
0,5
0,5
b) G i A là bi n c ch n đ c ba b n cùng môn ọ ế ố ọ ượ ạ
Ta có
n A C C C
3 3 3
4 5 6
( )= + +
=5+10+20 = 35
V y xác su t c a bi n c A là P(A) = ậ ấ ủ ế ố
35
455
0,077
0,5
0,5
c) G i B là bi n c không ch n đ c h c sinh nào gi i toán ọ ế ố ọ ượ ọ ỏ
⇒
B
là bi n c ch n đ c ít nh t m t h c sinh gi i toán ế ố ọ ượ ấ ộ ọ ỏ
n B C3
11
( ) 165= =
P(B) =
165 33
455 91
=
0,5
2
P(
B
) =
165 58
1455 91
− =
0,5
3a) +
( ) ( )
S SAB S SCD;� �
⇒ S là 1 đi mể
chung c a hai m t ph ng .ủ ặ ắ
+ m t khác ặ
AB CD/ /
nên giao tuy n c aế ủ
hai m t phăng s đi qua S và song song v iặ ẽ ớ
AB ho c CD.ặ
+ K Sẻm // AB v y ậ
( ) ( )
Sm SAB SCD=
0,25
0,25
0,25
b) Ba m t ph ng ặ ẳ
SAB SCD( ),( ),( )
α
c t nhau theo ba giao tuy n A’B’; Sắ ế n; B’D’
A'B' // Sn A'B' // AB
A'D' // Sm A'D' // AD
( ) ( )
ABCD/ /
α
0,25
0,25
c) OI là đ ng trung bình c a tam giác SAC nên OI // SA ườ ủ
SA SAB( )
OI // (SAB)
0,25
0,5
Dành riêng cho h c sinh c ban b nọ ơ ả
4a
a)
u u
s
1 5
4
2 0
14
+ =
=
u u
u u
1 5
1 4
2 0
4( ) 14
2
+ =
+
=
u u
u u
1 5
1 4
2 0
7
+ =
+ =
( )
u u d
u u d
1 1
1 1
2 4 0
( 3 ) 7
+ + =
+ + =
u d
u d
1
1
3 8 0
2 3 7
+ =
+ =
u
d
18
3
=
= −
0,25
0,25
0,25
b)
u
S10
10
10.(8 )
2
+
=
u10 8 9.( 3) 19= + − = −
S10 10.(8 19) 55
2
−
= = −
0,25
0,25
0,25
5a
5b a)
AB (3; 3)= −
uuur
M x y d( ; )∀
( )
';'')( yxMMTAB =
x x
y y
' 3
' 3
= +
= −
x x
y y
' 3
' 3
= −
= +
thay vào ph ng trình đ ngươ ườ
th ng d. Ta có nh c a đ ng th ng d qua phép t nh ti n theo véct ẳ ả ủ ườ ẳ ị ế ơ
AB
uuur
.
2(x’–3) + 3(y’+3) = 6
2x +3y = 3
0,25
0,25
0,5
b) A(–3;1), B(0;–2); I(–1;–2) . Ta có
x a x
y b y
' 2
' 2
= −
= +
G i A’(x’; y’); B’(xọ1’; y1’) là nh c a A và B qua phép đ i x ng tâm I ả ủ ố ứ
⇒ A’(1;–5), B’( –2;–2) 0,5
Dành riêng cho h c sinh nâng caoọ
Câu 4b a)
x 0 1 2 3
P(x) 0,216 0,432 0,288 0,064
b) E(X) = 1,2 V(X) = 0,72
1đ
0,5đ
3
n
m
I
O
B'
C'
D'
B
A
D
C
S
A'
================
4