S GIÁO D C- ĐÀO T OỞ Ụ Ạ
B C GIANGẮ
TR NG THPT PH NGƯỜ ƯƠ
S NƠ
Đ KI M TRA CH T L NGỀ Ể Ấ ƯỢ H C K IỌ Ỳ
NĂM H C 2011-2012Ọ
MÔN: TOÁN - KH I 11Ố
Th i gian: 90 phút (không k th i gian giao ờ ể ờ
đ)ề
Câu I. (1 đi m)ể
Cho đng tròn ườ (C) tâm I (1; 2) và bán kính R = 1. Tìm nh c a đng tròn ả ủ ườ (C) qua
phép t nh ti n theo vecto ị ế
( )
2; 1v= −
r
.
Câu II. (3,0 đi m)ể
Gi i các ph ng trình l ng giác sau:ả ươ ượ
1)
− + =
2
2 os 3 os 1 0;c x c x
2)
−=
1 sinx 0
sin4x
.
Câu III (2 đi m)ể
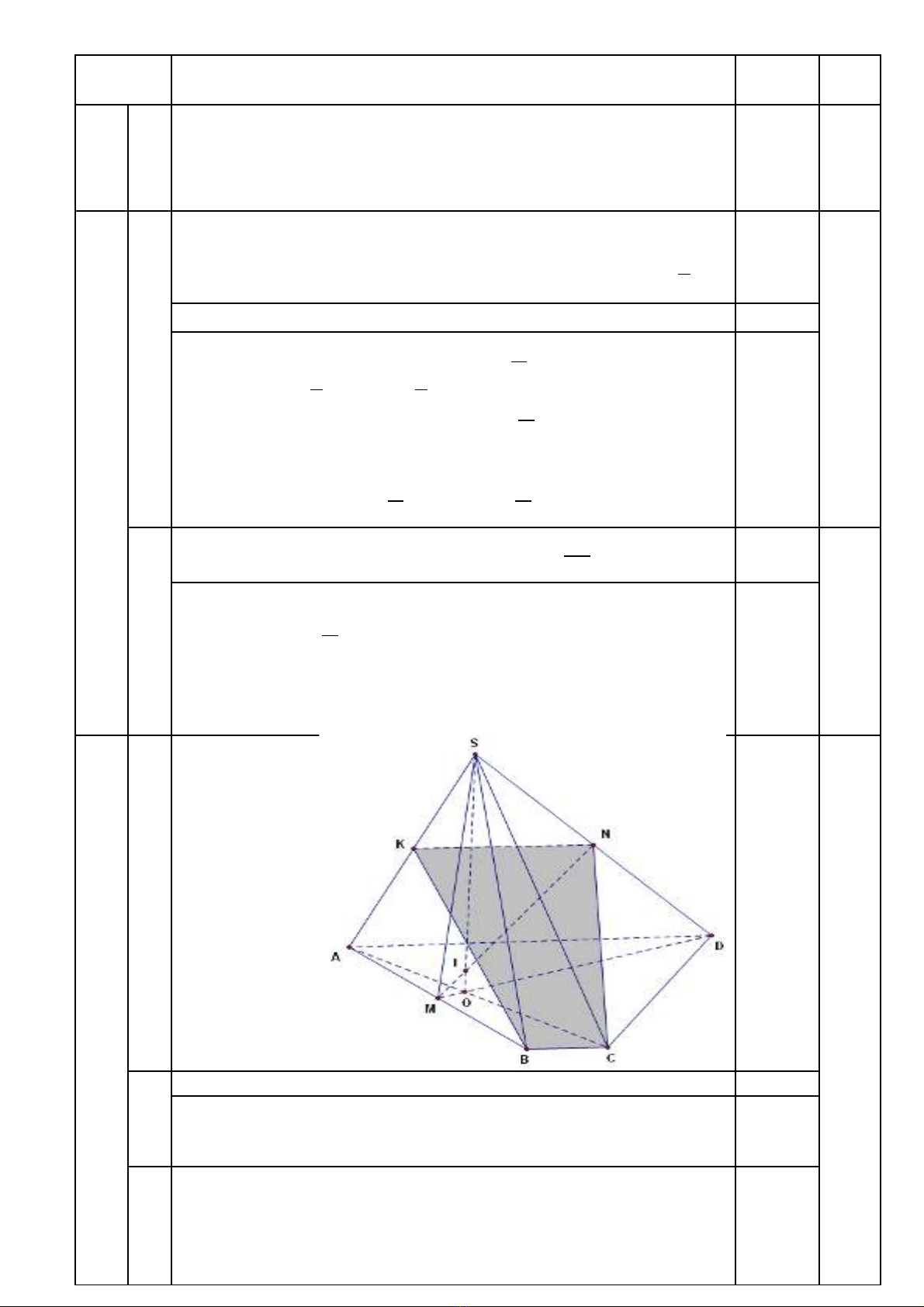
Cho hình chóp S.ABCD có đáy là hình thang ABCD (có đáy nh BC). G i M, Nỏ ọ
l n l t là trung đi m c a AB và SD, O là giao đi m cầ ượ ể ủ ể ủa AC và DM.
a/ Tìm giao đi m c a MN và m t ph ng (SAC).ể ủ ặ ẳ
b/ Tìm thi t di n c a hình chóp v i m t ph ng (NBC). Thi t di n đó là hìnhế ệ ủ ớ ặ ẳ ế ệ
gì ?
Câu IV. (1,5 đi m)ể
Trong cu c thi “Đ vui đ h c”, ph n thi v đích, đi A đc ch n ng uộ ố ể ọ ở ầ ề ộ ượ ọ ẫ
nhiên 3 câu h i t m t gói g m 15 câu h i thu c ba lĩnh ỏ ừ ộ ồ ỏ ộ v c: t nhiên, xã h i, hi uự ự ộ ể
bi t chung; m i lĩnh v c 5 câu h i.ế ỗ ự ỏ
1. H i đi A có bao nhiêu cách ch n câu h i.ỏ ộ ọ ỏ
2. Tính xác su t sao cho ba câu h i đc ch n có ít nh t m t câu thu c lĩnhấ ỏ ượ ọ ấ ộ ộ
v c t nhiên.ự ự
Câu V (1,5 đi m)ể
1. Tính t ng 10 s h ng đu tiên c a m t c p s c ng (uổ ố ạ ầ ủ ộ ấ ố ộ n) có công sai d, bi tế
+ =
=
1 10
10 20
1
u u
d
.
2. Ch ng minh r ng dãy sứ ằ ố
( )
n
u
v i ớ
7 5
5 7
n
n
un
+
=+
, là m t dãy s tăng và b ch n.ộ ố ị ặ
Câu VI (1 đi m)ể
Tính t ng sau: ổ
1 2 3 4 1
2. 3. 4. ... ( 1) . . .
n n
n n n n n
S C C C C n C
−
= − + − + + −
n là s t nhiên l n h n 2.ố ự ớ ơ
--------------------------------H T------------------------------------Ế
( HS không đc s d ng tài li u, cán b coi thi không gi i thích gì thêm)ượ ử ụ ệ ộ ả
ĐÁP ÁN Đ THI H C KÌỀ Ọ I – MÔN TOÁN L P 11 – C B N (2011-2012)Ớ Ơ Ả
CÂU N I DUNGỘĐi m ể
tp
T nổ
g
I
G i ọ
( )
'
( ) 2 1; 1 2 (3;1)
v
I T I= = + − + =
r
và (C’) là nh c a (C) quaả ủ
. V y (Cậ’) là đng tròn tâm Iườ ’ (3; 1) bán kính R = 1. Do đó (C’)
có ph ng trình: ươ
( ) ( )
2 2
3 1 1x y− + − =
.
0.5
0.5
1
III
1.)
Đt ặ
[ ]
= −�os , 1;1t c x t
ta đc ượ
=
− + = =
2
1
2 3 1 0 1
2
t
t t
t
0.5
1.5
π
= = =� � �1 os 1 2 ,t c x x k k Z
0.25
ππ
ππ
= +
= =� ��
= − +
2
1 1 3
os ,
2 2 2
3
x l
t c x l Z
x l
V y nghi m c a ph ng trình đã cho là ậ ệ ủ ươ
π π
π π π
= = + = − + Ζ�2 , 2 , 2 , ( )
3 3
x k x l x l k
0.5
0.25
2.)
Đi u ki n ề ệ
π
π
�۹۹�sin4x 0 4x k , (k Z).
4
k
x
0.5
1.5
Ph ng trình đã cho tr thành:ươ ở
sinx = 1 x = 2 , ( ).
2k k Z
ππ
+� �
K t h p v i đi u ki n, ph ng trình đã cho vô nghi m.ế ợ ớ ề ệ ươ ệ 1
III
0.25
2
a)
Trong m t ph ng ặ ẳ (SDM), g i ọI là giao đi m c a ể ủ MN và SO. 0.25
Ta có:
( )
� �
I MN
I SO SAC
. Suy ra I là giao đi m c n tìm.ể ầ 0.5
b)
Ta có:
( )
( )
( ) ( )
� �
//
BC NBC
BC SAD
N NBC SAD
0.5
Suy ra giao tuy n c a ế ủ (NBC) và (SAD) là đng th ng đi qua Nườ ẳ
và song song v i ớBC.
K đng th ng qua ẻ ườ ẳ N và song song v i BC c t ớ ắ SA t i ạK.
Ta có BC // NK
Thi t di n c n tìm là hình thang ế ệ ầ BCNK.0.5
IV
1. S cách ch n câu h i là m t t h p ch p 3 c a 15.ố ọ ỏ ộ ổ ợ ậ ủ
V y có ậ
3
15
455C=
cách ch n câu h iọ ỏ 0.5
1.5
2
G i A là bi n c “ba câu h i đc ch n có ít nh t m t câu thu cọ ế ố ỏ ượ ọ ấ ộ ộ
lĩnh v c t nhiên”.ự ự
A
là bi n c “ba câu h i đc ch n không có câu nào thu c lĩnhế ố ỏ ượ ọ ộ
v c t nhiên”.Ta có ự ự
( )
3
10
120n A C= =
.
( ) ( )
( )
120 24 0, 26
455 91
n A
P A n
= = =
Ω
Do đó xác su t đ ba câu h i đc ch n có ít nh t m t câu thu cấ ể ỏ ượ ọ ấ ộ ộ
lĩnh v c t nhiên là ự ự
( )
( )
24 67
1 1 0,74
91 91
P A P A= − = − =
.
1
V
1
Ta có
=
+ = + + =
� � =� �
� � �
= =
� � =
1
1 10 1 1
10
1
10 20 10 9 20 10
1 1 1
u
u u u u d u
d d d
0.5
0.5
1.5
T ng m i s h ng đu tiên c a c p s c ng đã cho làổ ườ ố ạ ầ ủ ấ ố ộ
( )
= + =
10
10. 1 10 55
2
S
2
Vi t l i công th c xác đnh ế ạ ứ ị
n
u
d i d ng ướ ạ
7 24 .
5 5(5 7)
n
un
= − +
T đó suy ra ừ
1
24 1 1
. 0 ( 1)
5 5 7 5( 1) 7
n n
u u n
n n
+
� �
− = − > ∀
� �
+ + +
� �
0.25
M t khác ta có ặ
( )
7
1 1 ,
5
n
u n < ∀
1 1
0 .
5 7 12
do n
� �
<
� �
+
� �
V y ậ
( )
n
u
là dãy s tăng và b ch n.ố ị ặ
0.25
VI
Ta có
1 0
1
. ;
n n
C n C
−
=
2 1
1
2 . ;
n n
C n C
−
− = −
...........
1 1 1
1
( 1) . . ( 1) . . ;
n n n n
n n
n C n C
− − −
−
− = −
0.5
1
C ng theo v các đng th c trên ta đc ộ ế ẳ ứ ượ
1 2 3 0 1 2 1
1 1 1 1
1
2 3 ... ( 1) ( ... ( 1) )
(1 1) 0.
n n n n
n n n n n n n n
n
C C C C n C C C C
n
−
− − − −
−
− + − + − = − + − + −
= − =
V y S = 0.ậ
0.5