ĐỀ KIỂM TRA 1 TIẾT HK2
MÔN: Toán 9
Đề 15
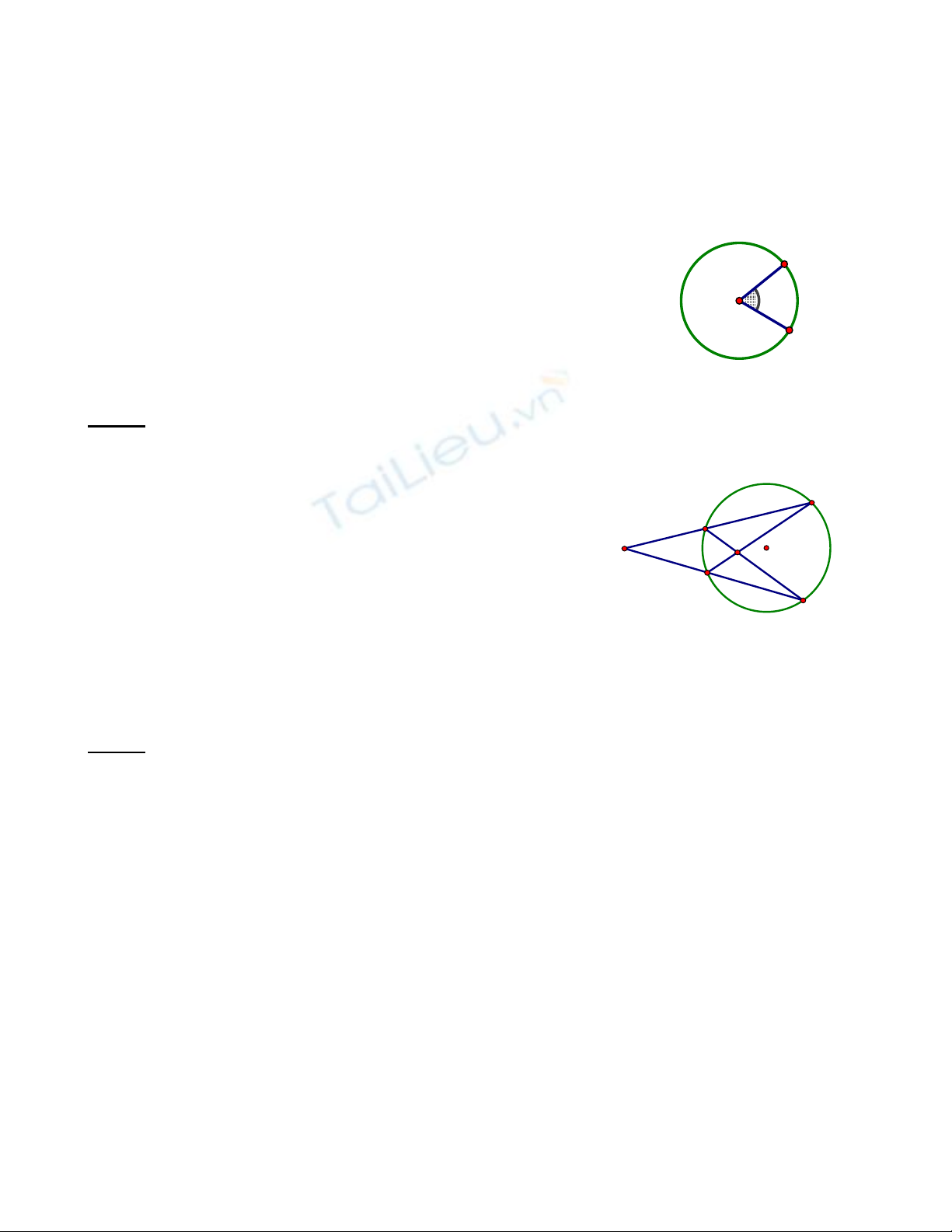
Câu 1: (1,5đ)
Cho hình vẽ. Tính số đo cung BmC, BnC
Câu 2: (4,5đ)
Cho hình vẽ, biết đường tròn tâm O bán kính 2cm,
sđ
AmC
= 400, sđ
BnD
= 1000
a. Tính
AMC , ANC
b. Tính độ dài cung AmC
c. Tính diện tích hình quạt BnDO
d. Chứng minh : NA . ND = NC . NB
Câu 3: (4đ)
Cho điểm M cố định nằm ngoài đường tròn (O). Kẻ tiếp tuyến MA, MB (A,B là tiếp
điểm)
a. Chứng minh tứ giác MAOB nội tiếp.
b. Vẽ cát tuyến bất kỳ MCD. Chứng minh: MA2 = MB2 = MC . MD
c. Gọi I là trung điểm của CD. Chứng minh I thuộc đường tròn ngoại tiếp tứ giác MAOB.
d. Khi cát tuyến MCD thay đổi thì điểm I chạy trên đường nào.
70°
nm
C
O
B
n
m
N
C
A
D
B
M
O
HƯỚNG DẪN CHẤM
Câu ý Nội dung Điểm
1
(1,5đ)
sđ
0
BmC BOC 70
0,75
sđ
0 0 0
BnC 360 70 290
0,75
2
(4,5đ)
a.
0 0
0
sdBnD sdAmC
AMC 2
100 40
30
2
0,75
0 0
0
sdBnD sdAmC 100 40
ANC 70
2 2
0,75
b.
AmC
Rn .2.40 4
l cm
180 180 9
1,0
c.
2
2
q(BnDO)
.R .n .2.100 10
S cm
360 180 9
1,0
d.
CM được :
ANB
CND
Suy ra hệ thức : NA . ND = NC . NB
0,5
0,5
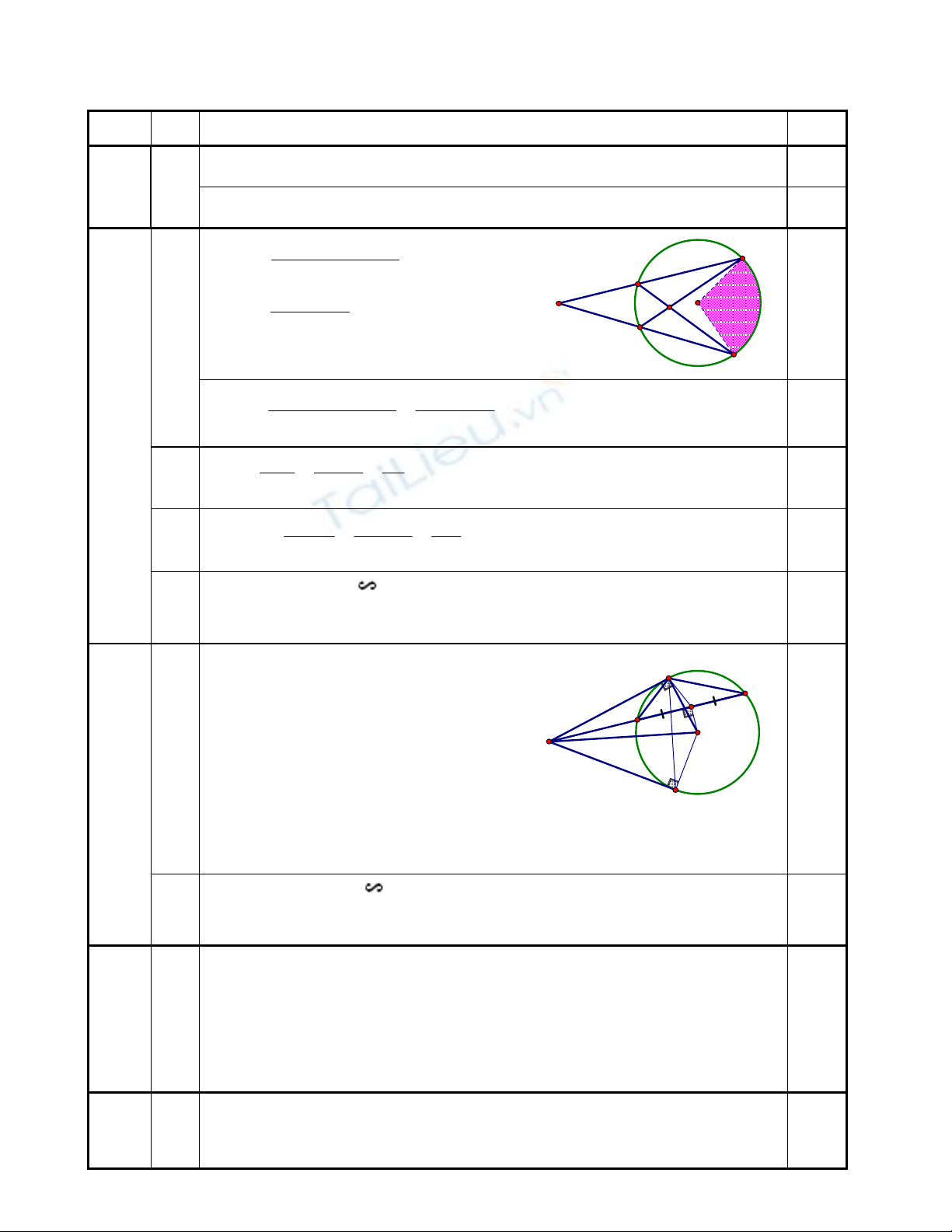
3
(4đ) a.
Theo t/c tiếp tuyến
Có
OA MA,OB MB
0
MAO MBO 90
Vậy tứ giác MAOB nội tiếp đường
tròn đường kjính MO.
0,5
0,5
b.
C/m được :
MAC
MDA
Suy ra hệ thức : MA2 = MB2 = MC . MD
0,5
0,5
c.
Có IC = ID
OI
CD (T/C đường kính và dây)
0
MAO MBO MIO 90
Nên A, I, B thuộc đường tròn đường kính MO
Vậy I thuộc đường tròn ngoại tiếp tứ giác MAOB.
0,5
0,5
d.
Có
0
MIO 90
, M và O cố định.
Nên I thuộc đường tròn đường kính MO.
0,5
I
B
C
A
O
M
D
n
m
N
C
A
D
B
M
O
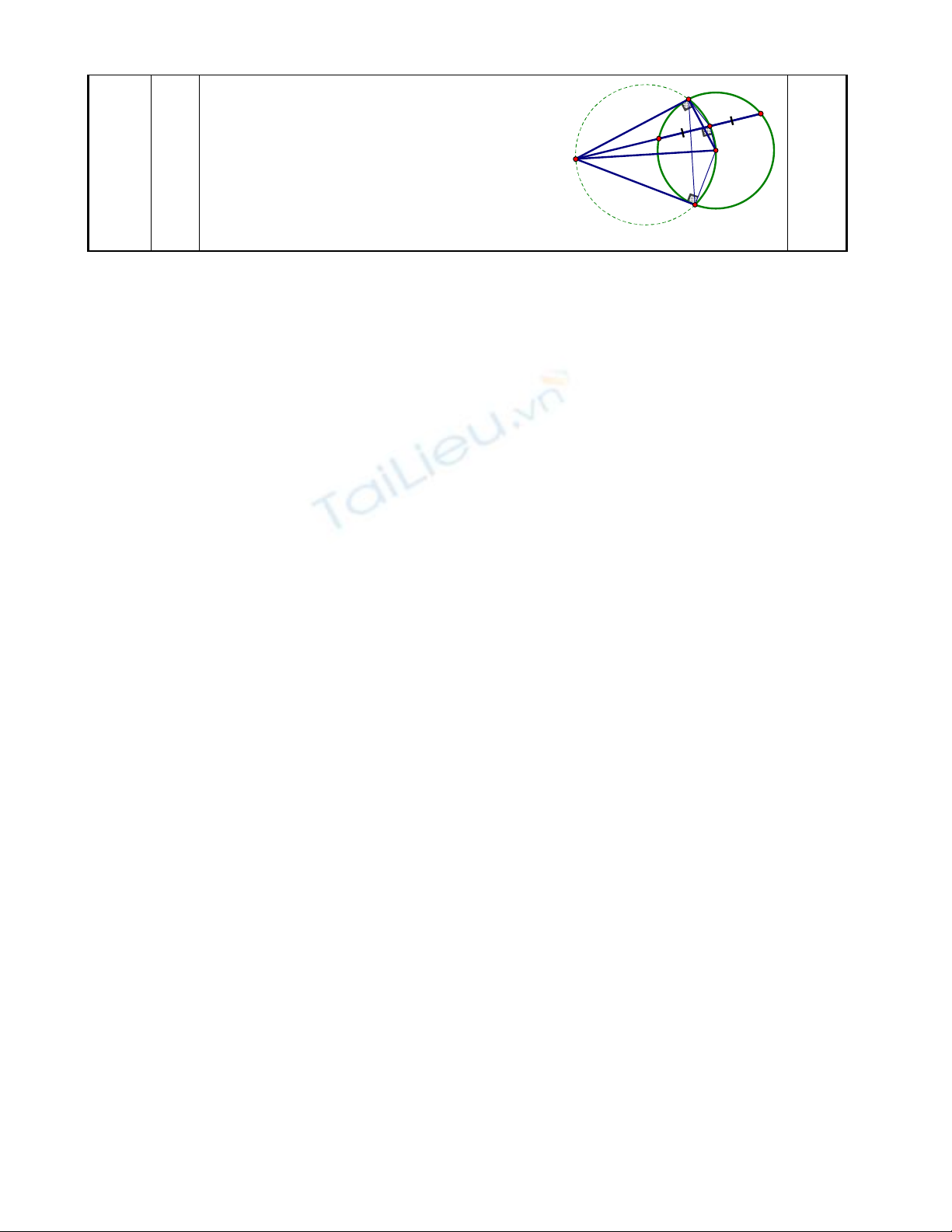
Giới hạn: Khi C
A thì I
A
Khi C
B thì I
B
Vậy I thuộc cung tròn của đường tròn
đường kính MO nằm trong đường tròn
tâm O.
0,5
I
B
C
A
M
O
D