
SỞ GD&ĐT VĨNH PHÚC
ĐỀ KTCL ÔN THI ĐẠI HỌC LẦN 1 NĂM HỌC 2013-2014
Môn: TOÁN; Khối D
Thời gian làm bài: 180 phút, không kể thời gian phát đề
I. PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7,0 điểm)
Câu 1 (2,0 điểm). Cho hàm số:
2
1
x
y
x
có đồ thị là (
C
).
a) Khảo sát sự biến thiên và vẽ đồ thị
( )C
của hàm số.
b) Tìm tất cả các giá trị thực của tham số
m
để đường thẳng
:
m
d y x m
cắt đồ thị (
C
) tại hai điểm
,A B
phân biệt sao cho độ dài đoạn thẳng
AB
nhỏ nhất.
Câu 2 (1,0 điểm). Giải phương trình: 2
(2 tan 1) cos 2 cos 2x x x
.
Câu 3 (1,0 điểm). Giải hệ phương trình:
4 2 2 2 3 2 2
3 2
2 5 2 1 0
x x y y y x y x
y x
( , ).x y R
Câu 4 (1,0 điểm). Tìm tất cả các giá trị thực của tham số
m
để phương trình: 22
m x x m
có hai
nghiệm thực phân biệt.
Câu 5 (1,0 điểm). Cho hình chóp .
S ABCD
có đáy
ABCD
là hình thang cân với
BC CD DA a
;
2AB a
; cạnh bên
SA
vuông góc với mặt phẳng
( )ABCD
;
SC
tạo với mặt phẳng
( )ABCD
một góc
bằng
0
60
. Tính thể tích của khối chóp .
S ABCD
và diện tích mặt cầu ngoại tiếp hình chóp .
S ABCD
theo
a
.
Câu 6 (1,0 điểm). Cho
, ,x y z
là các số thực dương thoả mãn: 2 2 2
1
x y z
. Tìm giá trị lớn nhất của
biểu thức: zyx
xzyzxyT
1
222 .
II. PHẦN RIÊNG (3,0 điểm). Thí sinh chỉ được làm một trong hai phần (phần A hoặc phần B)
A. Theo chương trình Chuẩn
Câu 7.a (1,0 điểm). Trong mặt phẳng với hệ trục toạ độ
Oxy
, cho hình chữ nhật
ABCD
có
4 2
AB ,
điểm
A
có hoành độ âm. Đường thẳng
AB
có phương trình
2 0
x y
, đường thẳng
BD
có phương
trình
3 0
x y
. Viết phương trình các đường thẳng chứa các cạnh còn lại của hình chữ nhật.
Câu 8.a (1,0 điểm). Trong mặt phẳng với hệ trục toạ độ
Oxy
, cho tam giác
ABC
đều. Đường tròn nội tiếp tam
giác
ABC
có phương trình 2 2
( 4) ( 2) 5
x y
, đường thẳng
BC
đi qua 3
;2
2
M
. Tìm toạ độ điểm
A
.
Câu 9.a (1,0 điểm). Cho số nguyên dương
n
thỏa mãn 2 1 2
4 6
n n
n n n
A C C n
. Tìm hệ số của
16
x
trong khai triển nhị thức Niu-tơn
32
n
x x
(với
0
x
).
B. Theo chương trình Nâng cao
Câu 7.b (1,0 điểm). Trong mặt phẳng với hệ trục toạ độ
Oxy
, cho các điểm
(4; 3); (4;1)
A B
và đường
thẳng
( ) : 6 0
d x y
. Viết phương trình đường tròn
( )C
đi qua
A
và
B
sao cho tiếp tuyến của (
C
) tại
A
và
B
cắt nhau tại một điểm thuộc
( )d
.
Câu 8.b (1,0 điểm). Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho elíp
E
đi qua điểm 3 2
; 2
2
M
và
có độ dài trục lớn bằng
6
. Tìm tọa độ của điểm
N
thuộc (
E
) sao cho
5
ON .
Câu 9.b (1,0 điểm). Cho số nguyên dương
n
thỏa mãn 3
2
20( 2)
n
A n
. Tìm số hạng không chứa
x
trong khai triển nhị thức Niu-tơn 3
1n
x
x
(với
0
x
).
-------------Hết------------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:…………………………………………Số báo danh:……………………………
SỞ GD&ĐT VĨNH PHÚC
(Đáp án có 06 trang)
ĐÁP ÁN KTCL ÔN THI ĐH LẦN 1 NĂM HỌC 2013-2014
Môn: TOÁN; Khối D
I. LƯU Ý CHUNG:
- Hướng dẫn chấm chỉ trình bày một cách giải với những ý cơ bản phải có. Khi chấm bài học sinh làm
theo cách khác nếu đúng và đủ ý thì vẫn cho điểm tối đa.
- Điểm toàn bài tính đến 0,25 và không làm tròn.
- Với bài hình học không gian nếu thí sinh không vẽ hình hoặc vẽ hình sai thì không cho điểm tương ứng
với phần đó.
II. ĐÁP ÁN:
Câu Ý Nội dung trình bày Điểm
1 a 1,0 điểm
+ TXĐ:
\ 1
D R
+ Sự biến thiên: Ta có: 2
10,
( 1)
y x D
x
. 0,25
+ Hàm số đã cho đồng biến trên các khoảng
( ;1)
và
(1; )
.
+ Hàm số không có cực trị
+ Giới hạn, tiệm cận.
1 1
lim ;lim
x x
y y
đồ thị hàm số có tiệm cận đứng là đường thẳng:
1x
.
lim 1;lim 1
x x
y y
đồ thị hàm số có tiệm cận ngang là đường thẳng
1y
;
0,25
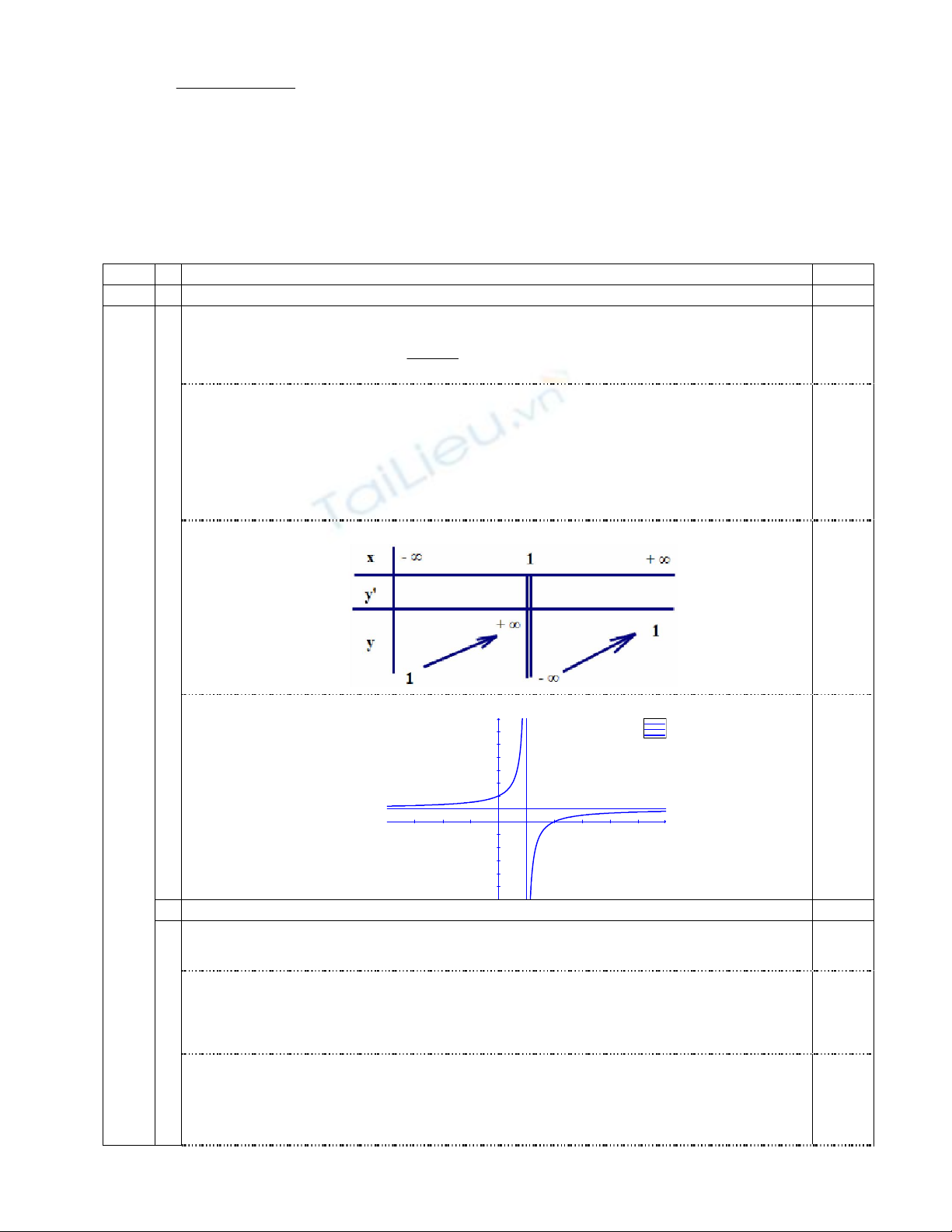
+ Bảng Biến thiên
+
+
0,25
+ Đồ thị hàm số cắt trục
Ox
tại điểm
(2;0)
, trục
Oy
tại điểm
(0;2)
f(x) =(x-2 )/(x-1)
f(x) =1
x( t)=1 , y( t)=t
-3 -2 -1 1 2 3 4 5
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
x
y
0,25
b 1,0 điểm
- Phương trình hoành độ giao điểm của
( )
m
d
và
( )C
là:
2
2 0
x mx m
(1) (
1x
). 0,25
Vì
2
4 8 0
1 2 1 0
m m
m m
với
m
nên (1) có 2 nghiệm phân biệt khác 1 với
m
.
Suy ra
( )
m
d
cắt
( )C
tại hai điểm phân biệt với
m
.
0,25
Gọi các giao điểm của
( )
m
d
và
( )C
là:
( ; ); ( ; )
A B B B
A x y B x y
với
A
x
;
B
x
là các nghiệm
của phương trình (1) . Theo Viet có:
2
A B A B
x x m; x x m
.
Ta có
2 2 2
2 2
2( ) 2 ( ) 4 . 2 4( 2) 2 ( 2) 4 8
A B A B A B
AB x x x x x x m m m
0,25

Vậy
AB
nhỏ nhất bằng
2 2
đạt được khi
2
m
. 0,25
2 1,0 điểm
Điều kiện:
cos 0 ( )
2
x x k k
Ta có:
2 2
2
2
(2tan 1)cos 2 cos2 3 cos 2 2cos 1
cos
x x x x x
x
0,25
3 2
2cos 3cos 3cos 2 0
x x x
Đặt
cos ; 0, 1;1
t x t t ta được: 3 2
1
2 3 3 2 0 2
1
2
t
t t t t
t
0,25
Với 1 cos 1 (2 1) ;
t x x k k Z
(thoả mãn).
Với
2t
(loại)
Với 1 1
cos 2 ;
2 2 3
t x x k k Z
(thoả mãn)
0,25
Vậy nghiệm của phương trình đã cho là:
(2 1)
k
;
2
3k
(
k Z
) 0,25
3 1,0 điểm
4 2 2 2 3 2 2
3 2
1
2 5 2 1 0 2
x x y y y x y x
y x
Đk:
5
2
x.
Phương trình 2 2 2
(1) ( 1 )( ) 0
x y x y
0.25
2
0
1
x y
x y
Trường hợp
0
x y
thế vào (2) không thoả mãn.
0.25
Trường hợp 2
1x y
thế vào phương trình (2):
3
2 3 2 1 0 3
y y
Xét hàm 3
3
( ) 2 3 2 1; ; 2
f t t t t
2
1
( ) 6
3 2
f t t
t
;
3
( ) 0; ; 2
f t t
Vậy hàm số
( )f t
đồng biến trên
3
;2
; mà
(1) 0
f
Suy ra phương trình (3) có nghiệm duy nhất
1y
0.25
Với 2
1 2 2
y x x
(thỏa mãn điều kiện)
Vậy nghiệm của hệ phương trình là:
( 2;1);( 2;1)
. 0.25
4 1,0 điểm
- Tập xác định:
D R
- Ta có:
2 2
2
x 2 1 x 2 1 ( )
x 2 1
x
m x m m x m f x
0.25
- Ta có:
2
2
2 2
2 x 2
'( )
x 2 x 2 1
f x
,
x R
0.25
22
2
2 2
2
2 x 2
'( ) 0 0 2 x 2 0
2
x 2 x 2 1
x
f x x
1
x
lim f ( x )
;
1
x
lim f ( x )
- Bảng biến thiên:
0
0
1
2
- 2
-1
_
+
_
+
2
- 2
-
f(x)
f'(x)
x
0.25
- Từ bảng biến thiên ta được
2; 1 1; 2
m thỏa mãn. 0.25
5 1,0 điểm
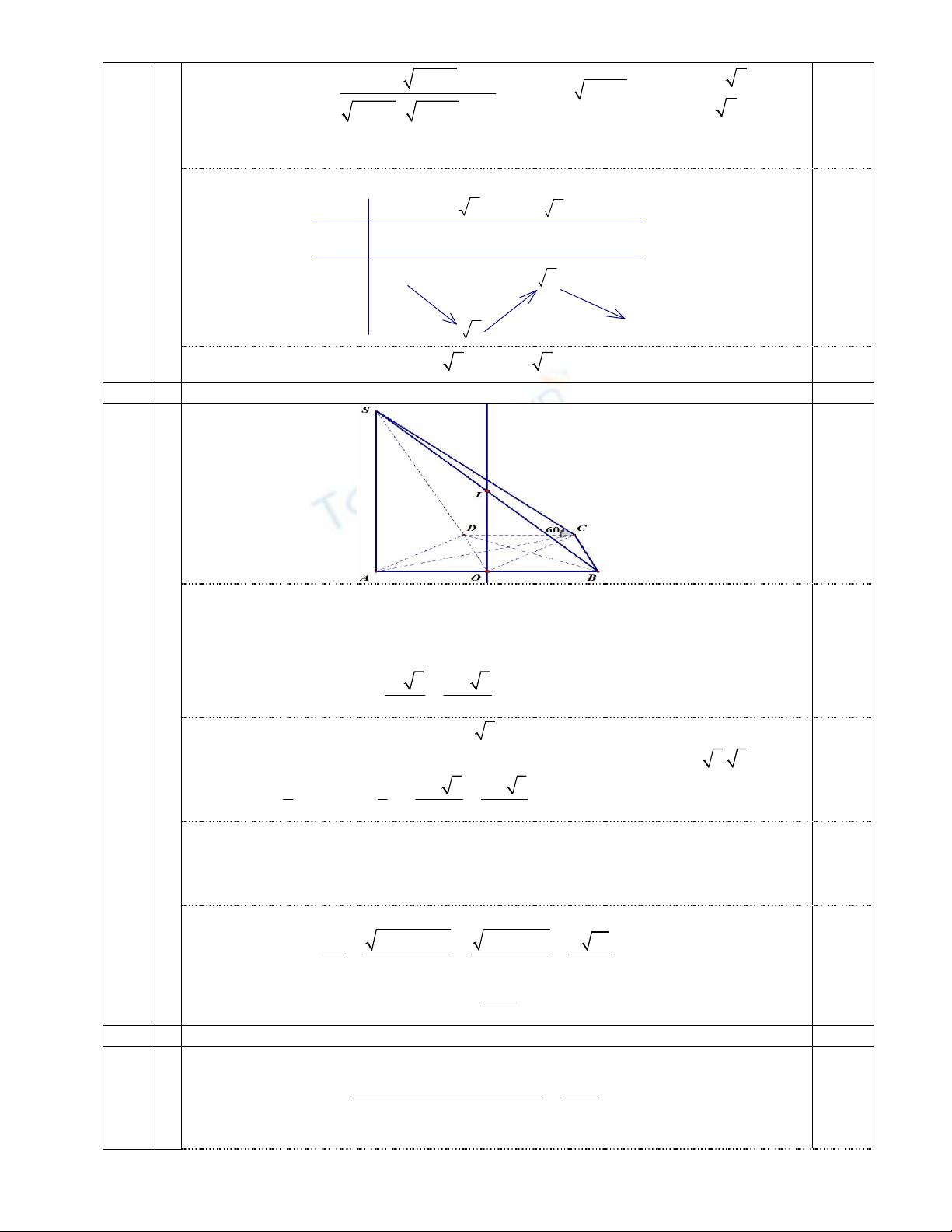
- Vì
BC CD DA a
;
2AB a
nên
AB
là đáy lớn;
DC
là đáy nhỏ của hình thang
ABCD
. Gọi
O
là trung điểm của
AB
.
- Ta có các tứ giác
DAOC
;
DOBC
là các hình thoi và các tam giác
DAO
;
DC
O;
OCB
là các tam giác đều cạnh
a
O
là tâm đường tròn ngoại tiếp
DABC
.
- Ta có:
2 2
3 3 3
3 3.
4 4
ABCD AOD
a a
S S (đvdt).
0.25
- Trong hình thoi
DAOC
, ta có:
3AC a
- Trong tam giác vuông
SAC
có góc
0
60
SCA
0
.tan 60 3. 3 3a
SA AC a
2 3
.
1 1 3a 3 3a 3
. . .3a.
3 3 4 4
S ABCD ABCD
V SA S (đvtt)
0.25
- Gọi
I
là trung điểm của
SB
O//SA
I
đường thẳng
OI
là trục của đường tròn
ngoại tiếp đa giác đáy nên
DIA IB IC I
.
- Mặt khác tam giác
SAB
vuông tại đỉnh
A
IS
IA IB
IS DIA IB IC I
hay
I
là tâm mặt cầu ngoại tiếp hình chóp .
S ABCD
.
0.25
- Bán kính của mặt cầu đó là:
2 2 2 2
9a 4a 13
IS
2 2 2 2
SB SA AB a
R IA IB
.
- Diện tích của mặt cầu đó là:
2
2 2
13a
4 4 13
4
R a
(đvdt)
0.25
6 1,0 điểm
- Đặt
0; ttzyx
- Ta có:
1
2
1
2
2222
2
t
tzyxzyx
zxyzxy
Lại có:
0
222 xzzyyx nên
222
23zyxzyx
0.25
33
2 tt .
- Khi đó:
t
tT 1
1
2 với
3;1t
- Xét hàm
t
ttf 1
1)( 2 với
3;1t;
2
1
2)(
t
ttf
;
3;1;0)(
ttf
0.25
- Ta có bảng biến thiên của hàm số trên
3;1
2 +
1
3
1
+
3
1
f(t)
f'(t)
t
0.25
- Từ bảng biến thiên suy ra
1
2
3
T , dấu “ = ” xảy ra khi 3
1
zyx
Vậy
T
lớn nhất bằng ( 3
1
2) đạt được khi 3
1
zyx .
0.25
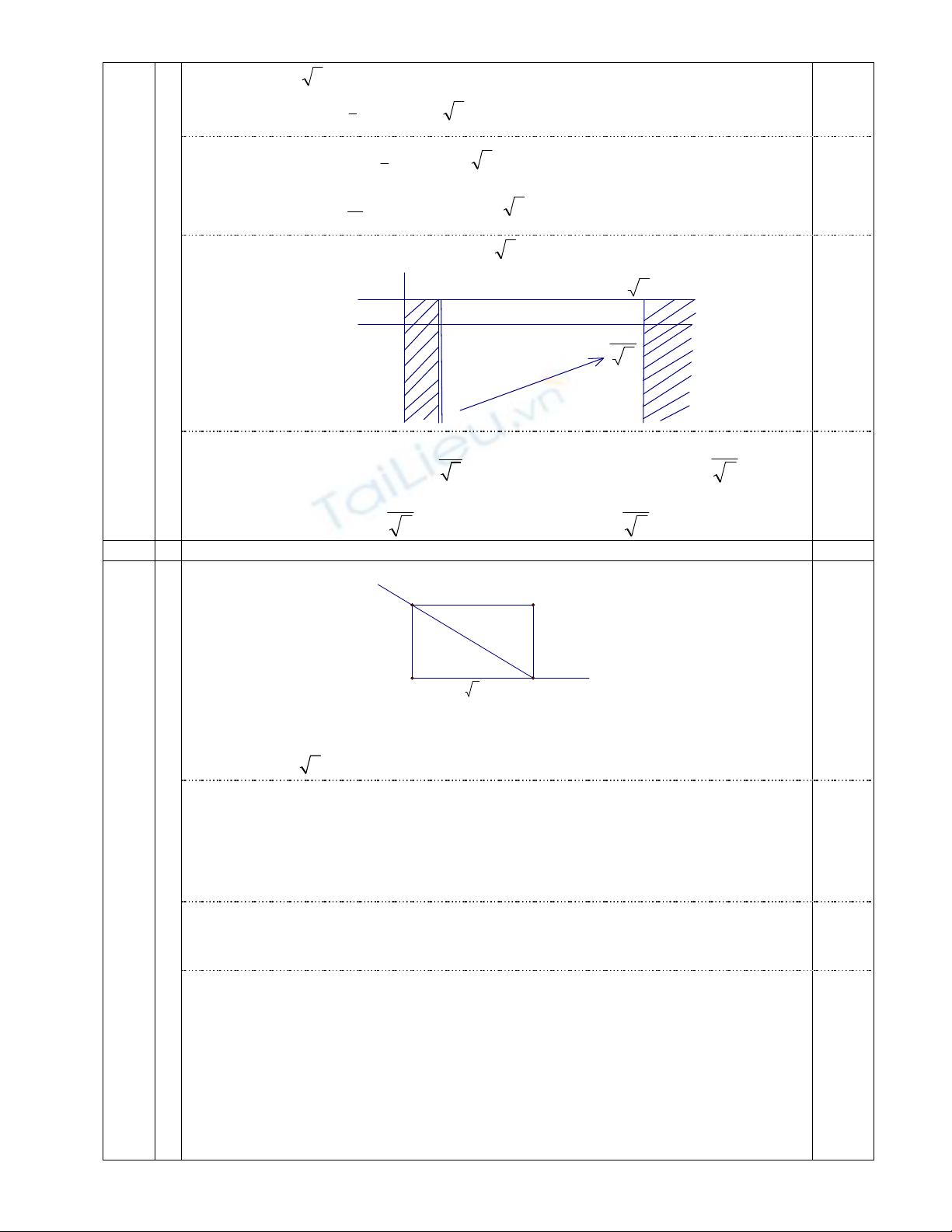
7.a 1,0 điểm
4 2
3x + y = 0
x + y + 2 = 0
DC
B
A
- Ta có:
(1; 3)
B AB BD B
+
( ; 2); ( 0)
A AB A t t t
- Ta có 2 2
4 2 ( 1) ( 1) 32
BA t t
0.25
2
3
( 1) 16 5
t
tt
Với
5t
loại vì
0t
.
Với 3 ( 3;1)
t A AD
qua
A
và vuông góc với
AB
nên có phương trình
( 3) ( 1) 0
x y
4 0
x y
.
0.25
- Đường thẳng
BC
qua
B
và vuông góc với
AB
nên có phương trình:
( 1) ( 3) 0 4 0
x y x y
.
+
D(-1:3)
D AD BD
0.25
- Đường thẳng
DC
qua
D
và song song với
AB
nên có phương trình :
( 1) ( 3) 0 2 0
x y x y
Vậy:
: 4 0;
BC x y
: 2 0
DC x y
;
: 4 0
AD x y
0.25



![Đề thi tiếng Anh tốt nghiệp THPT 2025 (Chính thức) kèm đáp án [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250627/laphong0906/135x160/9121751018473.jpg)








![11 chủ đề ôn tập môn Toán lớp 2 [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250613/phuongnguyen2005/135x160/74791749803387.jpg)



