Trang 1
ĐỀ LUYỆN THI ĐÁNH GIÁ NĂNG LỰC ĐẠI HỌC QUỐC GIA HÀ NỘI NĂM 2022
ĐỀ SỐ 10
Thời gian làm bài:
195 phút (không kể thời gian phát đề)
Tổng số câu hỏi:
150 câu
Dạng câu hỏi:
Trắc nghiệm 4 lựa chọn (Chỉ có duy nhất 1 phương án đúng) và điền đáp án đúng
Cách làm bài:
Làm bài trên phiếu trả lời trắc nghiệm
CẤU TRÚC BÀI THI
Nội dung
Số câu
Thời gian (phút)
Phần 1: Tư duy định lượng – Toán học
50
75
Phần 2: Tư duy định tính – Ngữ văn
50
60
Phần 3: Khoa học
10
60
10
10
10
10
Trang 2
PHẦN 1. TƯ DUY ĐỊNH LƯỢNG – Lĩnh vực: Toán học
Câu 1 (NB): Theo báo cáo thường niên năm 2017 của ĐHQG-HCM, trong giai đoạn từ năm 2012 đến năm
2016, ĐHQG-HCM có 5.708 công bố khoa học, gồm 2.629 công trình được công bố trên tạp chí quốc tế
và 3.079 công trình được công bố trên tạp chí trong nước. Bảng số liệu chi tiết được mô tả ở hình bên.
Năm nào số công trình được công bố trên tạp chí quốc tế chiếm tỷ lệ cao nhất trong số các công bố khoa
học của năm?
A. Năm 2013. B. Năm 2014. C. Năm 2015. D. Năm 2016.
Câu 2 (TH): Một vật rơi tự do có phương tình
22
1, 9,8 /
2
s gt g m s==
là gia tốc trọng trường. Vận tốc tức
thời của chuyển động tại thời điểm
11,5t=
giây là :
A.
112,2 /ms
B.
117,2 /ms
C.
127,7 /ms
D.
112,7 /ms
Câu 3 (NB): Phương trình
2 3 4
48
xx+−
=
có nghiệm là:
A.
2
3
B. 2 C.
6
7
D.
4
5
Câu 4 (TH): Hệ phương trình sau có bao nhiêu nghiệm?
32
1
2 3 6
xy
x x x
+ =
+ + =
A. 1 B. 2 C. 3 D. 4
Câu 5 (NB): Gọi
1
z
là nghiệm phức có phần ảo âm của phương trình
22 3 0zz+ + =
. Trên mặt phẳng tọa
độ, điểm nào sau đây là điểm biểu diễn của số phức
1
z
?
A.
( )
1; 2Pi−−
B.
( )
1; 2Qi−
C.
( )
1; 2N−
D.
( )
1; 2M−−
Trang 3
Câu 6 (TH): Trong không gian Oxyz, phương trình của mặt phẳng đi qua điểm
( )
2;2;3M
và vuông góc
với trục Oy là:
A.
2 0.y+=
B.
0.y=
C.
2 0.y−=
D.
5xz+=
Câu 7 (NB): Trong không gian Oxyz, hình chiếu vuông góc của điểm
( )
1;2;3A
trên mặt phẳng
( )
Oyz
có
tọa độ là:
A.
( )
0;2;3
B.
( )
1;0;3
C.
( )
1;0;0
D.
( )
0;2;0
Câu 8 (TH): Tập nghiệm của bất phương trình
10
32
x
x
+
−
là:
A.
3
1; 2

−


B.
(
3
; 1 ;
2

− − +

C.
(
3
; 1 ;
2

− − +


D.
3
1; 2

−

Câu 9 (TH): Số nghiệm của phương trình
2
2sin 2 cos2 1 0xx+ + =
trong
0;2018
là
A. 2018. B. 1009. C. 2017. D. 1008.
Câu 10 (VD): Trên một bàn cờ có nhiều ô vuông, người ta đặt 7 hạt dẻ vào ô đầu tiên, sau đó đặt tiếp vào
ô thứ hai số hạt nhiều hơn ô thứ nhất là 5, tiếp tục đặt vào ô thứ ba số hạt nhiều hơn ô thứ hai là 5,… và cứ
thế tiếp tục đến ô thứ
n
. Biết rằng để đặt hết số ô trên bàn cờ người ta phải sử dụng 25450 hạt. Hỏi bàn cờ
đó có bao nhiêu ô?
A. 98 B. 100 C. 102 D. 104
Câu 11 (TH): Hàm số
( )
Fx
nào sau đây là một nguyên hàm của hàm số
( )
2
3
43
x
fx xx
+
=++
?
A.
( )
2ln 3 ln 1F x x x C= + − + +
B.
( )
( )
ln 2 1F x x=+
C.
( )
1
ln 2
3
x
Fx x
+
=+
+
D.
( ) ( )( )
ln 1 3F x x x= + +


Câu 12 (VDC): Cho hàm số
( )
y f x=
, hàm số
( )
y f x
=
liên tục trên và có đồ thị như hình vẽ.
Bất phương trình
( )
3
f x m x x − −
(
m
là tham số thực) nghiệm đúng với mọi
( )
2;0x−
khi và chỉ khi:
A.
( )
0mf
B.
( )
2 10mf − −
C.
( )
2 10mf − −
D.
( )
0mf
Trang 4
Câu 13 (TH): Một vật chuyển động với vận tốc
( ) ( )
2
3 4 / ,v t t m s=+
trong đó
t
là khoảng thời gian tính
bằng giây. Tính quảng đường vật đó đi được trong khoảng thời gian từ giây thứ 3 đến giây thứ 10?
A.
994m
B.
945m
C.
1001m
D.
471m
Câu 14 (VD): Một người vay ngân hàng 200 triệu đồng với lãi suất 0,6%/tháng theo thỏa thuận cứ mỗi
tháng người đó sẽ trả cho ngân hàng 10 triệu đồng và cứ trả hàng tháng như thế cho đến khi trả hết nợ
(tháng cuối cùng có thể trả dưới 10 triệu đồng). Hỏi sau ít nhất bao nhiêu tháng thì người đó trả được hết
số nợ ngân hàng.
A. 19. B. 22. C. 21. D. 20.
Câu 15 (TH): Tập nghiệm của bất phương trình
33
log log 1xx+
là:
A.
1
0; 9



B.
1
;9

−

C.
1
0; 9


D.
1;
9

+

Câu 16 (TH): Cho hình phẳng
( )
D
giới hạn bởi các đường
sinyx=
,
0y=
,
0x=
,
x=
. Thể tích khối
tròn xoay sinh bởi hình
( )
D
quay xung quanh
Ox
bằng:
A.
1000
B.
2
C.
2
2
D.
2
1000
Câu 17 (VD): Gọi T là tập hợp tất cả các giá trị nguyên dương của tham số m để hàm số
42
21y x mx= − +
đồng biến trên khoảng
( )
3; +
. Tổng giá trị các phần tử của T bằng:
A. 9 B. 45 C. 55 D. 36
Câu 18 (TH): Số phức z thỏa mãn
( )
2 3 1 7 3z i iz i− + = + −
là
A.
14 8
55
zi=+
B.
42zi=−
C.
42zi=+
D.
14 8
55
zi=−
Câu 19 (TH): Trong mặt phẳng phức, tập hợp các điểm biểu diễn của số phức z thỏa mãn điều kiện
| 2| | |z i z+ = −
là đường thẳng
d
có phương trình
A.
2 4 13 0xy+ + =
B.
4 2 3 0xy+ + =
C.
2 4 13 0xy− + − =
D.
4 2 3 0xy− + =
Câu 20 (VD): Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có đỉnh
( ) ( )
2; 3 , 3; 2AB−−
, diện tích bằng
3
2
và trọng tâm G nằm trên đường thẳng
3 8 0xy− − =
. Tìm hoành độ điểm C, biết C có hoành độ dương.
A. 1 B. 2 C. 3 D. 4
Câu 21 (TH): Cho đường cong
( )
( )
( ) ( )
2 2 2
: 1 3 2 1 1 0C m x m m y m m x m+ + + + + − − =
. Giá trị của
m
để
( )
C
là đường tròn:
A.
1
3
m=−
B.
3m=
C.
1
3
m=
D.
3m=−
Trang 5
Câu 22 (VD): Cho
( )
1;2;3K
và phương trình mặt phẳng
( )
:2 3 0P x y− + =
. Viết phương trình mặt phẳng
(Q) chứa OK và vuông góc với mặt phẳng (P).
A.
3 6 5 0x y z+ − =
B.
9 3 5 0x y z+ − =
C.
9 3 5 0x y z+ + =
D.
3 6 5 0x y z− − =
Câu 23 (TH): Cho hình nón đỉnh
S
có bán kính đáy
2R=
. Biết diện tích xung quanh của hình nón là
25
. Tính thể tích khối nón?
A. π B.
5
3
C.
4
3
D.
2
3
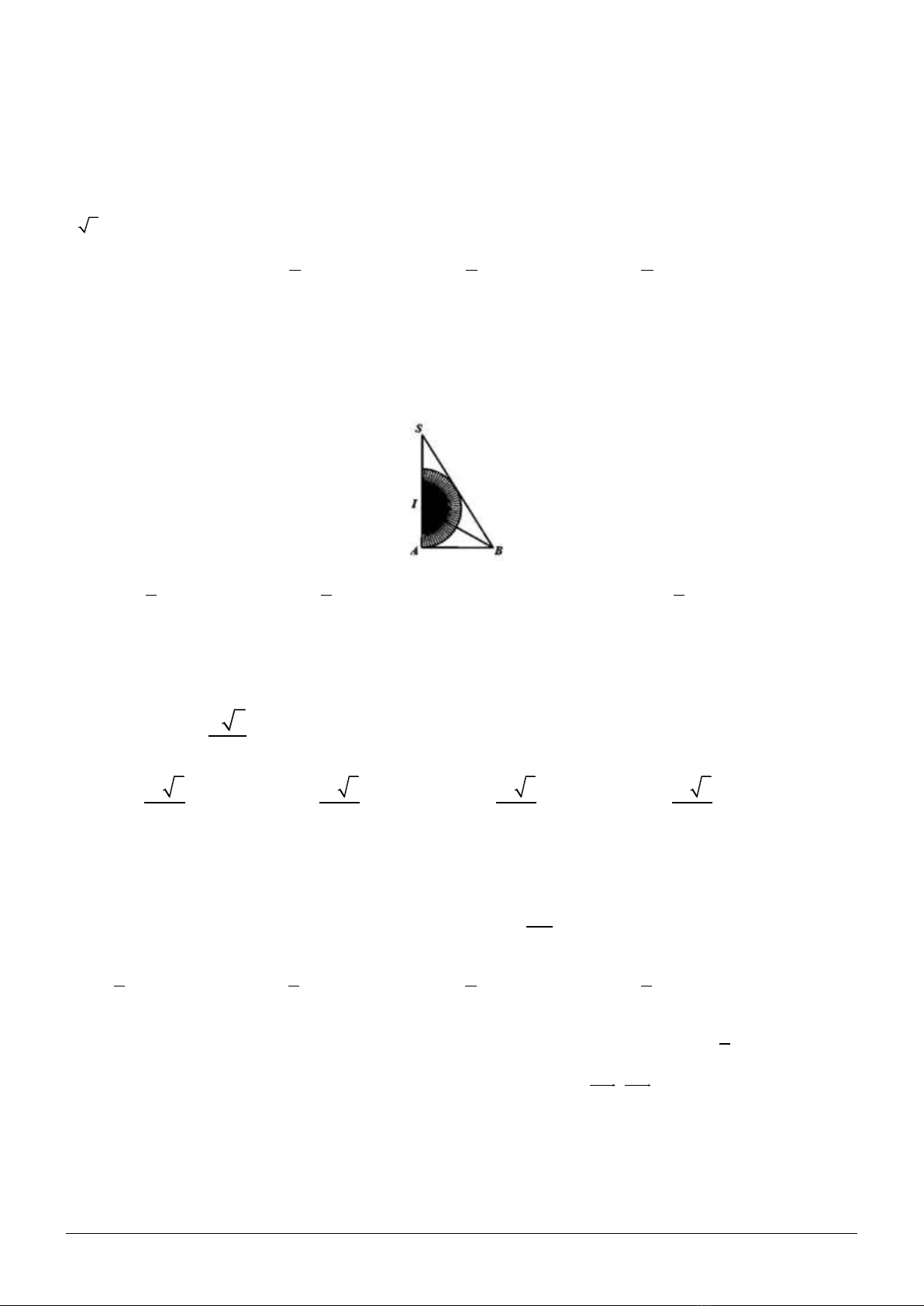
Câu 24 (VD): Cho tam giác
SAB
vuông tại
0
, 60A ABS=
. Phân giác của góc
ABS
cắt
SA
tại
I
. Vẽ nửa
đường tròn tâm
I
, bán kính
IA
(như hình vẽ). Cho miền tam giác
SAB
và nửa hình tròn quay xung quanh
trục
SA
tạo nên các khối tròn xoay có thể tích tương ứng là
12
,VV
. Khẳng định nào sau đây là đúng?
A.
12
4
9
VV=
B.
12
3
2
VV=
C.
12
3VV=
D.
12
9
4
VV=
Câu 25 (VD): Cho hình lăng trụ
.ABC A B C
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc của
điểm
A
lên mặt phẳng
( )
ABC
trùng với trọng tâm tam giác
ABC
. Biết khoảng cách giữa hai đường thẳng
AA
và
BC
bằng
3
4
a
. Tính theo
a
thể tích
V
của khối lăng trụ
.ABC A B C
.
A.
33
6
a
V=
B.
33
12
a
V=
C.
33
3
a
V=
D.
33
24
a
V=
Câu 26 (VD): Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm SD, điểm N
thuộc cạnh SA sao cho SN = 3AN . Đường thẳng MN cắt mặt phẳng (ABCD) tại P, đường thẳng PC cắt
cạnh AB tại K . Trình bày cách xác định điểm K và tính tỉ số .
A. B. C. D.
Câu 27 (VD): Trong không gian Oxyz, cho mặt cầu
2 2 2 9
( ): 2 4 2 0
2
S x y z x y z+ + + − − + =
và hai điểm
(0;2;0)A
, (2; 6; 2)B−−
. Điểm
( )
;;M a b c
thuộc
( )
S
thỏa mãn tích
MA MB
có giá trị nhỏ nhất. Tổng
abc++
bằng
A.
1−
B. 1 C. 3 D. 2
KA
KB
2
3
1
4
1
2
1
3