Trang 1
ĐỀ LUYỆN THI ĐÁNH GIÁ NĂNG LỰC ĐẠI HỌC QUỐC GIA HÀ NỘI NĂM 2022
ĐỀ SỐ 4
Thời gian làm bài:
195 phút (không kể thời gian phát đề)
Tổng số câu hỏi:
150 câu
Dạng câu hỏi:
Trắc nghiệm 4 lựa chọn (Chỉ có duy nhất 1 phương án đúng) và điền đáp án đúng
Cách làm bài:
Làm bài trên phiếu trả lời trắc nghiệm
CẤU TRÚC BÀI THI
Nội dung
Số câu
Thời gian (phút)
Phần 1: Tư duy định lượng – Toán học
50
75
Phần 2: Tư duy định tính – Ngữ văn
50
60
Phần 3: Khoa học
10
60
10
10
10
10
Trang 2
PHẦN 1. TƯ DUY ĐỊNH LƯỢNG – Lĩnh vực: Toán học
Câu 1 (TH):
Ở quốc gia nào, số giờ làm việc trung bình của người lao động nữ cao hơn những quốc gia còn lại?
A. Hy Lạp B. Hà Lan C. Anh D. Nga
Câu 2 (TH): Cho chuyển động xác định bởi phương trình
( )
42
13 2 4
4
S t t t t
−
= + − −
, trong đó t tính bằng
giây (s) và S tính bằng mét (m). Tại thời điểm nào, giá tốc của chuyển động đạt giá trị lớn nhất?
A.
3t=
B.
2t=
C.
2t=
D.
0t=
Câu 3 (NB): Tìm nghiệm của phương trình
( )
2
log 5 4x−=
.
A
7x=
B.
11x=
C.
21x=
D.
13x=
Câu 4 (TH): Nghiệm của hệ phương trình
1 2 1 2
2 1 1
1
xy
yx
xy
−+
+=
+−
−=
là
A.
31
;
43
xy
−
==
B.
41
;
33
xy
−
==
C.
31
;
43
xy==
D. Vô nghiệm
Câu 5 (VD): Trong mặt phẳng tọa độ
Oxy
, cho điểm
,,M N P
lần lượt là điểm biểu diễn của các số phức
2 3 ,1 2 , 3i i i+ − − +
. Tọa độ điểm
Q
sao cho tứ giác
MNPQ
là hình bình hành là
A.
( )
0;2Q
B.
( )
6;0Q
C.
( )
2;6Q−
D.
( )
4; 4D−−
Câu 6 (TH): Trong không gian
Oxyz
cho
( ) ( ) ( )
1;1; 2 , 2;0;3 , 2;4;1A B C−−
. Mặt phẳng đi qua A và vuông
góc với đường thẳng BC có phương trình là:
A.
2 6 0x y z+ − − =
B.
2 2 2 0x y z− + + =
C.
2 2 2 0x y z+ + − =
D.
2 2 0x y z+ − + =
Câu 7 (NB): Trong không gian
,Oxyz
hình chiếu vuông góc của điểm
( )
1; 2;3M−
lên mặt phẳng
( )
Oyz
là:
A.
( )
1; 2;3A−
B.
( )
0; 2;3A−
C.
( )
1; 2;0A−
D.
( )
1;0;3A
Câu 8 (NB): Bất phương trình
33
23
2 4 2 4
xxx
+ +
−−
tương đương với
Trang 3
A.
23x
B.
3
2
x
và
2x
C.
3
2
x
D. Tất cả đều đúng
Câu 9 (TH): Phương trình
2
sin 3sin cos 1x x x+=
có bao nhiêu nghiệm thuộc
0;3
.
A. 7 B. 6 C. 4 D. 5
Câu 10 (TH): Trên một cái bảng đã ghi sẵn các số tự nhiên từ 1 đến 2020. Ta thực hiện công việc như sau:
xóa hai số bất kì trên bảng rồi ghi lại một số tự nhiên bằng tổng của hai số vừa xóa, cứ thực hiện công việc
như vậy cho đến khi trên bảng chỉ còn một số. Số cuối cùng còn lại trên bảng là:
A. 4040 B. 2041210 C. 4082420 D. 2020
Câu 11 (TH): Họ nguyên hàm
223
1
xx
dx
x
++
+
bằng:
A.
2
2ln 1
2
xx x C+ − + +
B.
( )
2
2
1
21
xxC
x
+ − +
+
C.
2
2ln 1
2
xx x C+ + + +
D.
22ln 1x x x C+ + + +
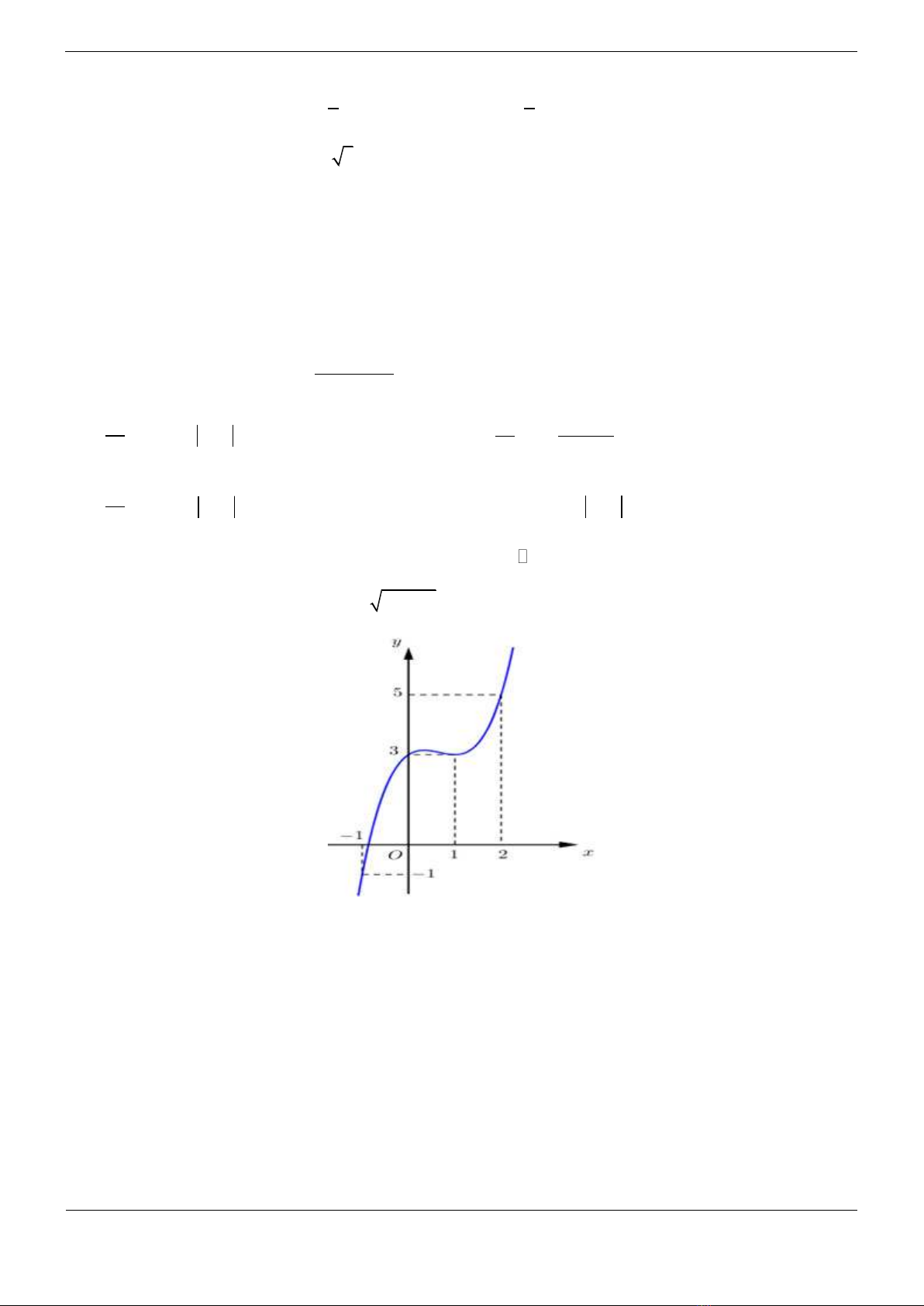
Câu 12 (VD): Cho hàm số
( )
y f x=
xác định, liên tục trên và có đồ thị như hình vẽ. Có bao nhiêu giá
trị nguyên của m để phương trình
()
2
22f x x m− − =
có nghiệm?
A. 6 B. 7 C. 3 D. 2
Câu 13 (VD): Một ô tô đang chạy với vận tốc
( )
15 /ms
thì tăng tốc chuyển động nhanh dần với gia tốc
( )
2
3 8 /a t m s=−
, trong đó t là khoảng thời gian tính bằng giây kể từ lúc tăng tốc. Hỏi sau 10 giây tăng
vận tốc ô tô đi được bao nhiêu mét?
A. 150 B. 180 C. 246 D. 250
Câu 14 (VD): Một người gửi 300 triệu đồng vào ngân hàng theo thể thức lãi kép kì hạn 1 quý và lãi suất
1,75% một quý. Hỏi sau ít nhất bao nhiêu tháng người gửi có ít nhất 500 triệu đồng (bao gồm cả vốn lẫn
lãi) từ số vốn ban đầu? (Giả sử lãi suất không thay đổi).
A. 81 tháng B. 30 tháng C. 45 tháng D. 90 tháng
Trang 4
Câu 15 (TH): Tập nghiệm của bất phương trình
( ) ( )
11
22
log 3 2 log 4xx− −
là
A.
2;3
3
S
=

B.
3
;2
S
= −


C.
23
;
32
S
=

D.
3;4
2
S
=

Câu 16 (TH): Hình bên vẽ đồ thị các hàm số
( )
221f x x x= − − +
và
( )
32
1 5 3 5
2 2 2 2
g x x x x= − − − +
. Diện
tích phần gạch chép trong hình bằng
A.
( ) ( ) ( ) ( )
11
31
f x g x dx g x f x dx
−
−−
− + −

B.
( ) ( ) ( ) ( )
11
31
g x f x dx f x g x dx
−
−−
− + −

C.
( ) ( ) ( ) ( )
11
31
f x g x dx f x g x dx
−
−−
− + −

D.
( ) ( ) ( ) ( )
11
31
g x f x dx g x f x dx
−
−−
− + −

Câu 17 (VD): Cho hàm số
18
2
mx
yxm
−
=−
. Gọi
S
là tập hợp các giá trị nguyên của tham số
m
để hàm số
đồng biến trên khoảng
( )
2; +
. Tổng các phần tử của
S
bằng:
A.
2−
B.
3−
C. 2 D.
5−
Câu 18 (VD): Biết
( )
,z a bi a b= +
là nghiệm của phương trình
( ) ( )
1 2 3 4 42 54i z i z i+ + − = − −
. Khi
đó
ab+
bằng
A. 27 B. -3 C. 3 D. -27
Câu 19 (VD): Tập hợp các điểm biểu diễn các số phức
z
thỏa mãn
12z i z i+ − = −
là:
A. Một đường thẳng. B. Một đường tròn. C. Một Parabol. D. Một Elip.
Câu 20 (VD): Trong mặt phẳng với hệ tọa độ
,Oxy
cho hình vuông
ABCD
có diện tích bằng 10 và
: 2 0, :3 0.A d x y CD x y − − = − =
Với
0
C
x
, số điểm
C
tìm được là
Trang 5
Câu 21 (TH): Cho hai đường tròn
( )
22
1:4C x y+=
và
( ) ( ) ( )
22
2: 2 2 1 2 2 6 0.C x y m x m y m+ − − − − + + =
Xác định
m
để hai đường tròn trên tiếp xúc ngoài với nhau.
A.
0m=
B.
2m=
C.
1m=
D.
3m=
Câu 22 (VD): Trong không gian
Oxyz
, viết phương trình của mặt phẳng
( )
P
biết
( )
P
đi qua hai điểm
( ) ( )
0; 1;0 , 1;1;1MN−−
và vuông góc với mặt phẳng
( )
Oxz
.
A.
( )
: 1 0P x z+ + =
B.
( )
:0P x z−=
C.
( )
:0Pz=
D.
( )
:0P x z+=
Câu 23 (TH): Cho hình nón có góc ở đỉnh bằng
0
120
và đường cao bằng 2. Tính diện tích xung quanh của
hình nón đã cho.
A.
16 3
B.
83
C.
43
D.
8
Câu 24 (VD): Một que kem ốc quế gồm hai phần : phần kem có dạng hình cầu, phần ốc quế có dạng hình
nón. Giả sử hình cầu và hình nón cùng có bán kính bằng
3,cm
chiều cao hình nón là
9.cm
Thể tích của que
kem (bao gồm cả phần không gian bên trong ốc quế không chứa kem) có giá trị bằng :
A.
( )
3
45 .cm
B.
( )
3
81 .cm
C.
( )
3
81 .cm
D.
( )
3
45 .cm
Câu 25 (VD): Cho hình lăng trụ
.ABC A B C
có
2 13AA a
=
, tam giác
ABC
vuông tại
C
và
0
30ABC=
, góc giữa cạnh bên
CC
và mặt đáy
( )
ABC
bằng
0
60
. Hình chiếu vuông góc của
B
lên mặt
phẳng
( )
ABC
trùng với trọng tâm của tam giác
ABC
. Thể tích của khối tứ diện
A ABC
theo
a
bằng:
A.
3
33 39
4
a
B.
3
9 13
2
a
C.
3
99 13
8
a
D.
3
27 13
2
a