S GIÁO D C - ĐÀO T OỞ Ụ Ạ Đ THI CH N H C SINH GI I B C PTTHỀ Ọ Ọ Ỏ Ậ
TH A THIÊN HU Ừ Ế NĂM H C 1998-1999.Ọ
----------------------- -------------------------------------------------
Đ CHÍNH TH CỀ Ứ MÔN: TOÁN B NG A VÒNG 1. Ả
SBD: (180 phút, không k th i gian giao đ )ể ờ ề
------------------------------------------------------------------------------------------------------------
Bài 1 ( 3 đi m)ể
Tìm c c tr c a hàm s :ự ị ủ ố
y = sin2x + cotg2
x
2
+ 4cos2
x
2
- 4sinx – 4cotg
x
2
( 0 < x < π).
Bài 2 ( 5 đi m)ể
Tìm giá tr l n nh t c a tham s m đ cho h ph ng trình sau có nghi m:ị ớ ấ ủ ố ể ệ ươ ệ
2 2
2 2 2
3
x xy y m
y yz z m
xy yz zx m
￬
￬+ + =
￬
￬
￬
￬+ + =
￬
￬
￬
￬+ + =
￬
￬
￬
( x, y, z ∈ R).
Bài 3 ( 6 đi m)ể
Cho t p h p: A = { a; a + 1; a + 2; a + n} v i a = 1998.ậ ợ ớ
Tìm t t c các giá tr nguyên d ng c a n đ t n t i hai t p h p B và C sao cho: Aấ ả ị ươ ủ ể ồ ạ ậ ợ
= B ∪ C và B∩C = ∅ mà t ng các ph n t c a t p B b ng các ph n t c a t p C.ổ ầ ử ủ ậ ằ ầ ử ủ ậ
Bài 4 (6 đi m) ể
Trong không gian cho ba m t ph ng c đ nh có m t đi m chung duy nh t. M làặ ẳ ố ị ộ ể ấ
m t đi m c a không gian, các đ ng th ng đi qua M song song v i hai m t ph ng c tộ ể ủ ườ ẳ ớ ặ ẳ ắ
m t ph ng còn l i l n l t t i A,B,C. Bi t MA + MB + MC = 1998.ặ ẳ ạ ầ ượ ạ ế
Tìm t p h p các tr ng tâm c a tam giác ABC.ậ ợ ọ ủ
H NG D N CH M VÀ BI U ĐI MƯỚ Ẫ Ấ Ể Ể
Đ THI H C SINH GI I T NH NĂM H C 1998-1999.Ề Ọ Ỏ Ỉ Ọ
MÔN TOÁN 12 B NG A, VÒNG 1.Ả
Bài 1(3 đi m). y = sinể2x + cotg2
x
2
+ 4cos2
x
2
- 4sinx – 4cotg
x
2
(0.5đ) + Đ t z = sinx +ặ cotg
x
2
; z2 = sin2x + cotg2
x
2
+ 4cos2
x
2
. Do đ ó: y = z2 – 4z.
(0.5đ) + y’x = y’z . z’x = (2z – 4)(
2
1
osx - 2sin
cx
2
) = 2(sinx + cotg
x
2
- 2)
2
os osx + 1
osx - 1
c x c
c
-
.
(0.5đ) + Do: 0 < x < π ⇒ cosx < 1 ⇒
2
os osx + 1
osx - 1
c x c
c
-
< 0
Nên: y’ cùng d u v i: - sinx -ấ ớ cotg
x
2
+ 2
(0.5đ) + Đ t t = tgặ
x
2
suy ra: - sinx - cotg
x
2
+ 2 =
2
2 2
2t 1 (t 1)(2t t 1)
2
1 t t t(1 t )
- - - +
- + =
+ +
.
(0.5đ) + Tam th c 2tứ2 – t + 1 luôn d ng v i m i t vì có bi t s âm; ươ ớ ọ ệ ố
0< x < π nên 0<
x
2
<
2
p
⇒ t(1 + t2) > 0.
Do đó: y’ cùng d u v i t – 1.ấ ớ
(0.5đ) + y’ = 0 ⇔ t – 1 = 0 ⇔ tg
x
2
= 1 ⇔ x =
2
p
( vì 0< x < π).
V y: hàm s có đi m c c ti u (ậ ố ể ự ể
2
p
; -4).
Bài 2 (5 đi m). ể
(1.5đ) + Đ t: X = x +ặ
y
2
; Y =
3
2
y; Z =
3
2
(y + z); T =
1
2
(z – y).
Ta đ c: ượ
2 2 2 2
x xy y X Y+ + = +
;
;
3(xy yz zx) XZ YT
2+ + = +
.
Do đó ta có h ệ
2 2
2 2 2
3
X Y m
Z T m
3
XZ YT m
2
￬
￬
￬
￬+ =
￬
￬
￬
￬+ =
￬
￬
￬
￬
￬
￬+ =
￬
￬
￬
.
(1.5đ) + Chú ý: (X2 + Y2)(Z2 + T2) = (XZ + YT)2 + (XT – YZ)2
x 0
2
p
π
tg
x
2
-1 - 0 +
y’ - 0 +
y
-4
Do đó: H đã cho có nghi m thì:ệ ệ
m.m2 ≥
2
3 3 3 3
3 4 4
m m (m ) 0 0 m
2 3 3
� �
￬
￬￬￬ - ￬� ��
￬￬
￬￬
￬
� �
Suy ra: m ≤
3
4
3
.
(1.75đ)+ Xét m =
3
4
3
. Ta có h : ệ
(1)
(2)
(3)
3
2 2 2
XT YZ
3
XZ YT m
2
Z T m
￬=
￬
￬
￬
￬
￬
￬+ =
￬
￬
￬
￬
￬+ =
￬
￬
￬
T (1) có th đ t X = uZ, Y = uT, thay vào (2) và (3) ta có: u = ừ ể ặ
3m
2
.
Do đó ta có h : ệ
y
hay y
2 2 2 2
2
2
32m 3
X mZ x
22m
3 m 2
Y mT z
2 m
Z T m m
y3m 4m 4
￬
￬￬
￬+
￬￬
=
￬=
￬
￬￬
￬￬
￬￬
￬￬+
￬
� �
= =
� �
� �
� �
� �
� �
+ =
� � =
� �
� � + +
� �
￬
￬
￬
v i m = ớ
3
4
3
.
(0.2 5đ) + T đó:ừ
Đáp s c a bài toán là m = ố ủ
3
4
3
.
Bài 3 (6 đi m). ể
(1.5 đ) + N u A = B ế∪ C và B∩C = ∅ mà t ng các ph n t c a B b ng t ng các ph nổ ầ ử ủ ằ ổ ầ
tử
c a t p C nên t ng: ủ ậ ổ
1998 + (1998 + 1) + ...+ ( 1998 + n) = 1998(n + 1) +
n(n 1)
2
+
là s ch n, suy ra ố ẵ
n(n 1)
2
+
l à s ch n, suy ra n(n + 1) chia h t 4 . ố ẵ ế
Do đó n có d ng n = 4k + 3 ho c d ng n = 4k (k ạ ặ ạ ∈ N).
(1.5 đ) + N uế n = 4k + 3 (k ∈ N): Lúc đó t p A có 4(k+1) ph n t . Chia A thành k + 1ậ ầ ử
t p ậ
con r i nhau, m i t p con g m 4 s t nhiên liên ti p.ờ ỗ ậ ồ ố ự ế
Ta bi t r ng m i b 4 s t nhiên liên ti p luôn chia đ c thành hai t p conế ằ ỗ ộ ố ự ế ượ ậ
có t ng các ph n t c a hai t p đó b ng nhau. Ví d : b n s a, a + 1, a + 2, aổ ầ ử ủ ậ ằ ụ ố ố
+ 3 thì a + ( a + 3 ) = ( a + 1 ) + ( a + 2 ). V y t n t i hai t p B và C th a bàiậ ồ ạ ậ ỏ
toán.
(3 đ) + N uế n = 4k (k ∈ N*): Lúc đó tp A có 4k + 1 ph n t . ậ ầ ử
Gi s A = B ả ử ∪C và B∩C = ∅ thì trong B ho c C có m t t p không ít h n 2kặ ộ ậ ơ
+
1 ph n t . Gi s B có không ít h n 2k+1 ph n t thì C có không quá 2k + 1ầ ử ả ử ơ ầ ử
ph n t . ầ ử
Ký hi u : SệB là t ng các ph n t c a B thì:ổ ầ ử ủ
SB ≥ 1998 + (1998 + 1) + ...+ ( 1998 + 2k) = 1998(2k+1)+ k(2k+1)
SC là t ng các ph n t c a C thì:ổ ầ ử ủ
SC ≤ (1998+ 2k+1) + (1998+2k+2) + ...+ (1998 + 4k) = 19982k + k(6k+1)
Theo gi thi t đ Sả ế ể B = SC nên:
1998.2k + k(6k+1) ≥ 1998(2k+1) + k(2k+1)
⇔ 6k2 + k ≥ 1998 + 2k2 + k ⇔ 4k2 ≥ 1998
2
1998
k k 23
4
�۳
.
+ Nu k = 23 ế⇒ n = 92.
T p A = {1998, 1998 + 1, 1998 + 2, ..., 1998 + 92}.ậ
v i Bớ = {1998 + 1, 1998 + 2,..., 1998 + 46, 1998 + 59}
C = {1998, 1998 + 47, ..., 1998 + 58, 1998 + 60,..., 1998 + 92}
Thì SB = SC = 95046.
+ N u k > 23. Ta có: A = Aế1∪A2. Trong đó:
A1 = {1998, 1998 + 1,..., 1998 + 92}
A2 = {1998 + 93, 1998 + 94,..., 1998 + 4k}.
Theo trên A1 chia đưc thành hai t p con r i nhau th a bài đ ra. ợ ậ ờ ỏ ề Còn t p Aậ2
g m (4k - 9z) ồ= 4(k – 23) ph n t . Lý lu n nh ph n a, t p Aầ ử ậ ư ầ ậ 2 cũng chia đ cượ
thành hai t p con th o bài ra. Nh v y t p A chia đ c hai t p con B và C,ậ ả ư ậ ậ ượ ậ
không giao nhau và t ng các s trong B b ng t ng các s trong t p C.ổ ố ằ ổ ố ậ
K t lu n: n có d ng 4k+3(kế ậ ạ ∈N) hay 4k(k∈N, k ≥ 23).
Bài 4 ( 6 đi m)ể
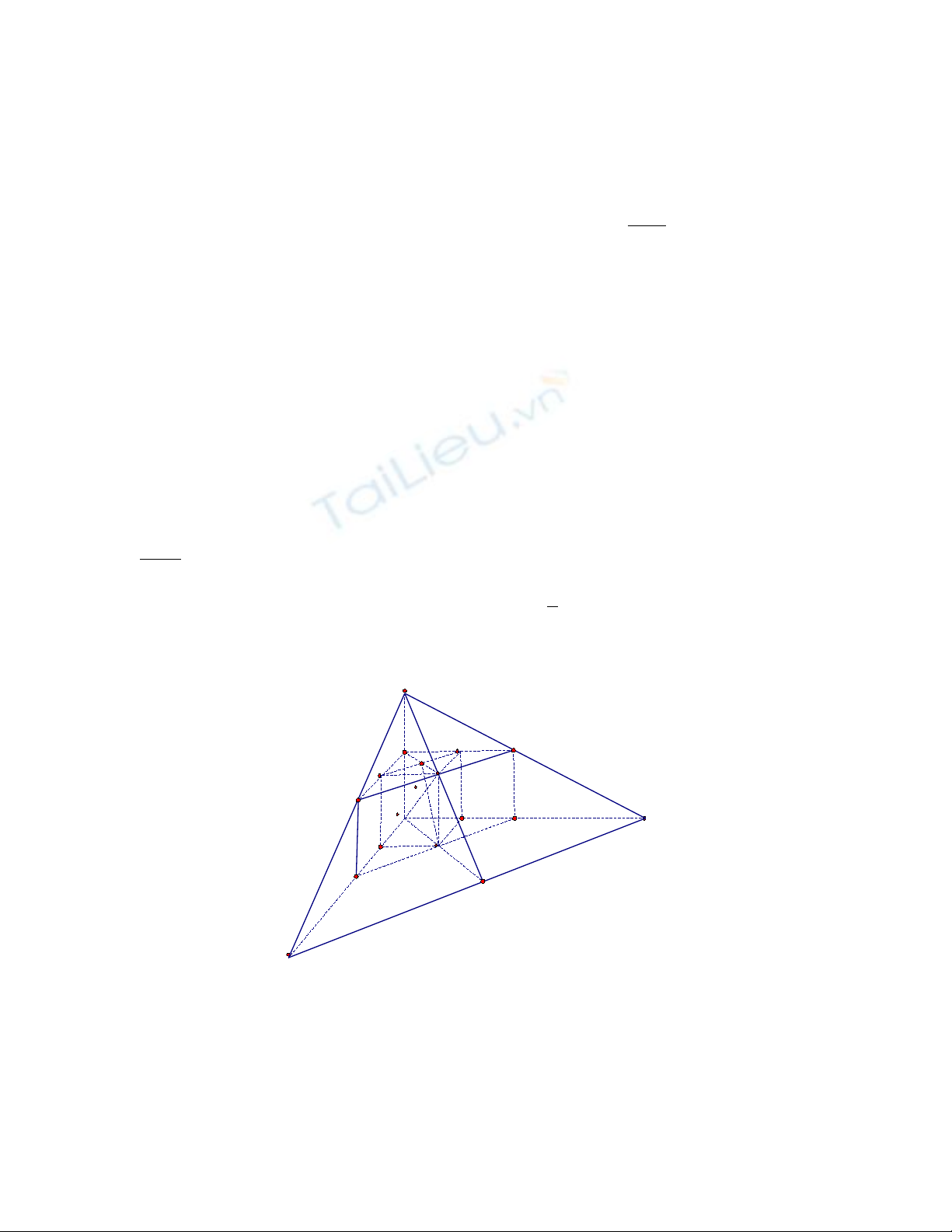
(1.5 đ) + G i O là giao đi m c a 3 m t ph ng. a, b, c là 3 giao tuy n . Dùng tính ch t hìnhọ ể ủ ặ ẳ ế ấ
h p và tính ch t tr ng tâm, ta có: ộ ấ ọ
2
OM ' OM
3
=
uuuur uuur
, v i M” là tr ng tâm c aớ ọ ủ
∆ABC.
(4đ) + Tìm t p h p các đi m M: ậ ợ ể
Ba m t ph ng chia không gian làm 8 mi n. Ta ch c n xét m t mi n: G i U, V, ặ ẳ ề ỉ ầ ộ ề ọ Ư
thu c a, b, c: OU = = OV = 1998.ộ Ơ
Ch ng minh đ c: M thu c mi n trong tam giác UV khi và ch khi:ứ ượ ộ ề Ư ỉ
OM WxOU yOV zO= + +
uuur uuur uuur uuur
v i x + y + z = 1.ớ
Mà MA + MB + MC = 1998 ⇔ x + y + z = 1.
Do đó: T p các đi m M là mi n trong c a tam giác UV .ậ ể ề ủ Ư
_U
_C
_V
_M'
_O
_M
_A
_C
_B
(0.5 đ) + Suy ra các đi m M’ ( tr ng tâm c a tam giác ABC) là nh c a mi n trong tamể ọ ủ ả ủ ề
giác
UV qua phép v t tâm O t 2/3.Ư ị ự ỉ