
TRU'ONG
£>AI
HOC
SU'
PHAM
KY
THUA,
T
THANH
PH6
H6
CHI
MINH
KHOA CO KHf
CHET
~O
MA.
Y
B0
MON
CO
SO
THIET Kt
MA
y
Cau
1:
(1,5 diem)
BE
THI
cu61
KY
HQC KY 2 NAM HQC 19-20
Mon:
Ca
ky
thuit
...
....
............................................. .
Mamon
h9c:
ENMEl30620
..
........
..
..
.
..
............... ....... .
E>@
s6/Ma
d@:
01 .
..
..
..
..
.......
E>@
thi c6 02 trang.
Thai gian: 90 phut.
E>uqc
phep sir
d11ng
tai li~u:
01
ta
gi~y A4 vi~t tay.
M(\t banh
r1\ng
chju lire
nhu
tren Hinh
1.
Bi~t lire
Fi
nlim
trong m~t phling Oyz, lire F
2 nlim
trong khong gian va c6 cac t9a
de;\
g6c
nhu
tren hinh ( 0<90°).
a) Bieu di~n cac vector lire tren du6i
d!IJlg
vector Descartes (theo cac vector
dan
vi T,],k),
b) Tim vector hqp lire
FR
(du6i d1
mg vector Descartes) cua hai lire
Fi
va F
2;
c) Tim
de;\
16-n
ctia vector
FR.
z
Hinh 1
Cau 2: (1,5 diem)
z
F=200N
r<--75
mm
.,,..,,.
1
I
¢1
Hinh2
Tay quay
ABC
duqc dung
d~
quay
tr11c
OA
nhu tren Hinh 2. Tf\lc
OA
nilm
d9c theo
tr11c
Oy,
AB
d6ng thai vuong g6c v6i
Oy
va BC. Lire F = 200 N tac
d11ng
t~i
C va vuong g6c v6i
tay
dm
BC
. Bi~t 0 = 60° va ¢ = 30°.
a) Bieu di~n vector lire F du6i d1
mg vector Descartes;
b) Tim d~ng vector Descartes ctia moment do lire F gay ra quanh tam
O.
Cau 3: (1,5.di~m)
Beam
AB
is
subjected to the loads and constraints as shown
in
Figure 3. Determine
reactions at A and
B.
Cau
4:
(2,0 di~m)
Figure 3.
Ca
du
ctia
mc;\t
may ep
Ion
duqc mo hinh h6a
nhu
tren Hinh 4.
Mc;\t
lire F = 300 N tac
d11ng
t~i
B theo
phuang
vuong g6c v6i tay
dm
BC. B6 qua ma sat, hay:
a) Ve
sa
d6 giai ph6ng,lien ket (FBD) cho tay
c!m
ABC;
b) Tim phan lire lien ket
t~i
A;
S6 hi~u: BMI/QT-PE>BCL-RE>TV Trang: 1/2
y

c) Tim lµc ep do con trugt C ep len
Ion.
B 0,3 m
A~
02m
,
Hinh 4 Hinh 5
Cau
5:
(2.5 di€m)
Cho he hai banh rang an
khcrp
nhu tren Hinh
5.
Bi~t R1 = 400 mm,
R2
=
OA
= 300 mm.
Tl!i
thoi di€m khao sat nhu tren hinh ve, tay quay
OA
va banh rang I dang quay nguqc chi€u kim
d6ng h6 quanh ch6t ban
IS
c6 djnh
t(li
O
vcri
v~
t6c g6c tmmg ung
la
% A
=IO
rad/s va
w,
= 5 rad/s, hay xac djnh:
a)
V~n
t6c cila di€m A;
b)
V~n
t6c cila di€m B;
C)
Tam
v~n
t6c tuc thoi cua banh rang 2; d)
V~n
t6e g6e cila banh rling 2.
Cau
6:
(I
di€m)
The disk shown
in
Figure 6, which has a mass
of
20 kg,
is
subjected to the couple moment
of
M =
80
N.m. The radius
of
gyration
of
the disk about its mass center O
is
k0 = 0,2 m.
lfthe
disk
starts from rest, determine its angular velocity when
it
has made I 0
revolutions.
Figure6
-
HET-
Ghi
chu
: Can
b9
coi
thi
kh6ng
au(J'c
giai
thich
ai
thi.
Chuan
dau
ra
cua
hoc oh
fi
n
(v
~ ki~n thuc)
[CDR I.
I]:
Thu
g.;m
duqc m9t he
h,rc
ve m9t tam thu
gQn
, phan tieh
duqc cac thanh ph/in phan lµc lien
k€t
(k€
ca
lire
ma sat) va
th
i
€t
l~p
duqc cac ohuong trinh can
bin
!!
eua
ehftt
di
€
m,
cua
v~t
ri1n
, he
v~t
rlin.
(CDR 1.2] : Tinh duqc cac thong so d9ng
hQe
(vi tri,
v~
to
e,
gia toe)
cua
v~t
rlin, di€m
thm;,c
v~t
rlin
tron
!!
chuv
€n
d9n g song
phi1n
g.
(CDR 1.
3]
:
Su
d11ng
duqc phuang ph~p luqng va ph!l'ang phap
nl\ng luqng
d€
xac djnh duqc thong so d9ng
hQc
cua
v~t
ran trong
chuv
€n
d9ng song
ohin
!!
ducri
tac
d11n
g cila
lµc.
(CDR 2.1]: Phan tich va mo hinh h6a duqc so co M tinh djnh
trong ca khi
bi1n
g cac mo hinh tinh
tuan
!!
un
g.
(CDR 2.2]: Phan tich va mo hinh h6a duqc so ca cau phang trong
ca khi
bi1n
g cac mo hinh tinh
tUOD
!!
uni!.
fCDR
3.11:
DQc
hieu cac tai
li~u
ca
hQc
ban
!!
tie1rn
Anh.
Noi
dun
2 kiem
tra
Cau
I,
2,
3, 4
Cau
5,
6
Cau6
Cau
3,4
Cau4,
5
Cau
3,6
Ngay
IO
thang
07
n1im
2020
Thong qua
bl}
mon /::r
(Icy
va ghi ro h9 ten)
S6
hi~u:
BMI/QT-PDBCL-RDTV
T
61.M~
T,>.,:,
4':
ang: 2/2

DAP
AN
DE
THI
CUCH
KY
HK2-NH 19-20
TRVONG
O~I
HQC
SV
P~M
KY
THUA T
THANH PHO HO CHI MINH Mon: Ca ky thu~t ... ................................................. .
KHOA
CO
KHi
CHE
TAO
MAY
B()
MON
co
so
THIET.KE
MAY Ma
n;ion
hQ~:
ENME 130620 ······················ ................. .
08
s6/Ma
de:
01
......... ...........
DA
c6 03 trang.
Cau
1:
1,50 d
a) •
F,
=(200{1
5
3)1-(200{:!}
N
76,9]-184,6k
N 0,75 d
•
cos0=-Jl-cos
2
(60°)-cos
2(120°) = (0
<90°)
2
• F
2 = (350)(cos60"
)1
+ (350)(cosl20°
)}
+
(350{
~}
N
=175t-175}+247,5f
N
b) t. =
1151
-98,1}
+ 62,9f 0,50 d
• N
c) 0,25 d
F• = + (-98,1) 2 +62,92 = 210,2 N
Cau 2: 1,50 d
• F =
(Fcos¢)i
+0]-(Fsin¢)k
= 173,2i -IOOk N
0,50d
•
i;,
10
=OC=(l50cos60")i
+(100+75)}+(150sin60")k
mm
0,50 d
• i'c,o =
75i
+ 175] + 129,9k
mm
• M0 = i'c,o x F =
-I
7500i
+30000}-303
I0,9k = N.mm 0,50 d
Cau3:
1,50 d
S<1d6GPLK: 0,50 d
y
2000Nlm~t
L
A,
A . . - - • -, • 1- I B
X 600N.ml-c-
Ay
4m
•--2m
.......
Phu<1ng
trinh can
bing
cho d§m AB:
•
F.
= (0,5)(2000 N/m)(6 m) = 6000 N 0,75 d
•
_LF,
=0
A,
-N
8 sin30° = 0
Ax
-0,5N
8 = 0
(I)
• L
FY=
0
AY
-F,
1 + N8 cos30° = 0 AY
-6000+
= 0 (2)
•
_LMA
= 0
(F.)(2
m) + 600
N.m-(N
8 cos30°)(6 m) = 0
=0
(3)
S6 hi~u:
BM
1/QT-POBCL-ROTV Trang:
1/3
Giai
ra
cac
uhan
I!!£
lien k~t: 0,25 d
Ax=l212
,4 N·
' AY
=3900
N;
NB
=2424,9 N
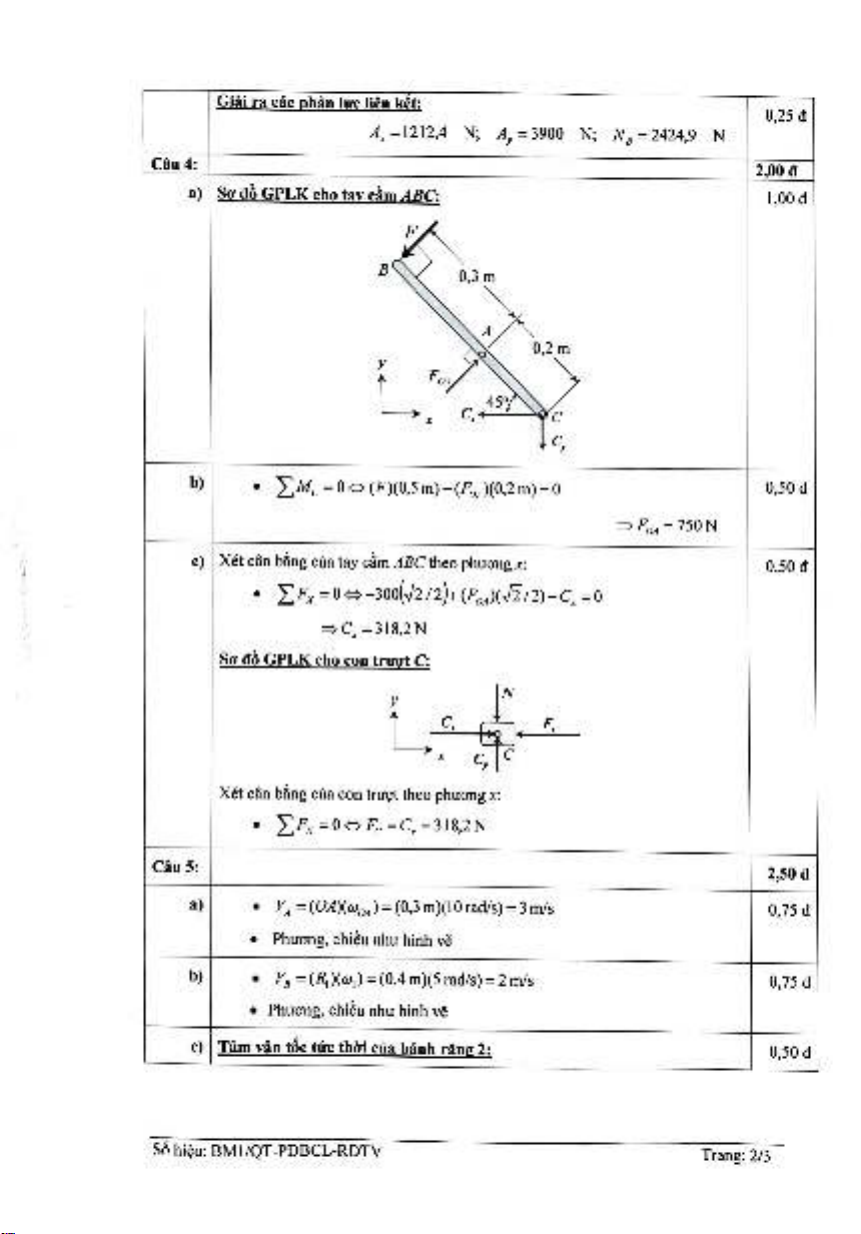
Cau4: 2,
00d
a)
SO'
d6 GPLK cho tay
dm
ABC:
1,00d
F
B 0,3 m
0 0,
2m
LF
()A
45° I
X c , l
c,.
b)
•
LM
c = 0 (F)(0,5
m)-(F
0A)(0,2 m) = 0 0,50 d
=750N
c) Xet can
bing
clia tay
dim
ABC theo phucmg
x:
0,50 d
•
LFx
=0
SO'
d6 GPLK cho con
tr!!Q'.!
C:
y~
Lxcx
Cy C
Fe
Xet can
bing
clia con trugt theo phucmg x:
•
LF
x
=0~F
c =Cx
=318,2N
Cau
5:
2,50 d
a) •
VA
=(OA)(%A)=(0,3m)(!0rad/s)=3m/s
0,75 d
• Phucmg, chi~u nhu hinh ve
b)
• V
8 = (R1
)(m
1) = (0,4 m)(5 rad/s) = 2
mis
0,75 d
• Phucmg, chi~u nhu hinh
ve
c)
Tam van t6c
tfrc
thin cua banh rang
2:
0,50 d
S6
hi~u: BM
1/QT-PE>BCL-RE>TV
Trang: 2/3

d)
10)
-~-~
2-
-
rA
II
C
r8/I
C
rA
II
C -
r8/I
C =
0,1
m
0)
2 =
IO
rad/s ( chi€u nhu hinh
ve)
Cau
6:
Dong nang:
•
T,
= 0 (Ca
h~
dung yen)
I 2 2 2
• T2 =
-(mk
0
)(J)
= 0,4 (J)
2
Cong cua ngoai
hrc:
Sa
d6
GPLK (FBD)
Iu
1
_2 =
M.0
= (80 N.m)[(l0)(21r) rad]=
1600Jr
J
Iu1-2
=5026,55 1
Ap
dung dinh ly dong nang:
T,
+
Iu,_2
=
T2
(J) =
112,1
rad/s
Ghi chu: Sinh vien
c6
Mi giai khac dap
an
nhung
dung vdn c6 didm t6i
da
.
-HET-
0,50 d
1,00 d
0,50 d
0,25 d
0,25 d
S6
hi~u:
BMI/QT-POBCL-ROTV Trang: 3/3


























