TRƯỜNG THPT THỦ ĐỨC
1
ÔN TẬP GIỮA HỌC KỲ I LỚP 11 MÔN TOÁN NĂM HỌC 2022 – 2023
ĐỀ 01
Câu 1. Cho hàm số
y f x xác định trên và có bảng biến thiên như hình bên duới
a) Hãy mô tả chiều biến thiên của hàm số
f x trên π 7π
;
3 6
.
b) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
f x trên π 5π
;
6 3
.
c) Tìm nghiệm của phương trình
24 3 0f x f x với π 5π
;
3 3
.
d) Giải phương trình
23 2 0
cos3 1
f x f x
x
với π 7π
;
6 6
x
.
Câu 2. Tìm tập xác định của các hàm số sau
a) 2 3
cos 1
x
yx
b) 5
sin 1
3
x
y
x
c) 3tan 4
7
y x
Câu 3. Giải các phương trình sau
a) 2cos 2 3 0
7
x
(ĐS: 41 29
, ,
84 84
x k x k k
)
b) 2
sin 2cos 2 0x x (ĐS: 2 ;x k k
)
c) 2
2sin 3sin2 3x x (ĐS: ;
3
x k k
)
d) 2
cos5 cos cos4 cos 2 3cos 1x x x x x với
;x
e) 1 1
sin 2 sin 2cot 2 0
2sin sin 2
x x x
x x
Câu 4. Nhiệt độ trung bình hằng ngày T (tính bằng độ Fahrenheit) tại Kansas City, Missouri, Mỹ
được mô hình bởi công thức 2
54 25,2sin 4,3
12
t
T
trong đó t được đo bằng tháng và
0t ứng với ngày 1 tháng 1. Hỏi nhiệt độ trung bình hằng ngày cao nhất và thấp nhất là bao
nhiêu?
Câu 5. a) Trong một lớp học có 18 học sinh nam và 17 học sinh nữ. Hỏi có bao nhiêu cách để giáo
viên gọi ngẫu nhiên 4 học sinh lên bảng sao cho có cả nam và nữ? (ĐS: 46920)
TRƯỜNG THPT THỦ ĐỨC
2
b) Từ các chữ số 0, 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên chẵn có ba chữ số?
(ĐS: 168)
c) Từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8 có thể lập được bao nhiêu số tự nhiên có năm chữ số khác
nhau và nhất thiết phải có chữ số 1 và 5 (ĐS: 2400)
ĐỀ 02
Câu 1. Cho hàm số
y f x
xác định trên
và có bảng biến thiên như hình bên duới
a) Hãy mô tả chiều biến thiên của hàm số
f x
trên π;
π
2
.
b) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
f x
trên 3
π
0;
2
.
c) Tìm nghiệm của phương trình
2
2 3 0
f x f x
với
π 3π
;
2 2
x
.
d) Giải phương trình
2
2 cos 1 1
f x x
với
π 3π
;
2 2
x
.
Câu 2. Tìm tập xác định của các hàm số sau
a)
4 5
2sin 2
x
yx
b)
cot 2
4
y x
c) 2
3tan
2 4
x
y
Câu 3. Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau
a)
9 2sin 7
y x
b) 4 2
sin 2cos 1
y x x
Câu 4. a) Tìm tất cả các giá trị thực của
m
để phương trình
4sin 1 cos
x m x m
có nghiệm.
b) Gọi
T
là tập giá trị của hàm số
3sin
cos 2
x
y
x
. Hỏi trong
T
có bao nhiêu số nguyên?
Câu 5. Giải các phương trình sau
a)
o
tan 40 3 0
x
b)
sin 1 sin 2 0
x x
c) 2
2cos 3sin 3 0.
x x
d) 2 2
cos 3sin cos 2sin 1
x x x x
e)
sin9 3cos9 2 0
x x
f)
2sin 1 cos2 sin 2 1 2cos
x x x x
TRƯỜNG THPT THỦ ĐỨC
3
Câu 6. a) Từ 20 câu hỏi trắc nghiệm gồm 9 câu dễ, 7 câu trung bình và 4 câu khó người ta chọn ra 10
câu để làm đề kiểm tra sao cho phải có đủ cả 3 loại dễ, trung bình và khó. Hỏi có thể lập được
bao nhiêu đề kiểm tra (ĐS: 176451)
b) Có bao nhiêu chữ số chẵn gồm bốn chữ số đôi một khác nhau được lập từ các số 0, 1, 2, 4, 5,
6, 8 ? (ĐS: 520)
c) Từ các số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên, mỗi số có 6 chữ số đồng thời
thỏa điều kiện: sáu số của mỗi số là khác nhau và trong mỗi số đó tổng của 3 chữ số đầu nhỏ
hơn tổng của 3 số sau một đơn vị (ĐS: 108)
ĐỀ 03
Câu 1. Cho hàm số
y f x có đồ thị như hình bên duới
a) Hãy mô tả chiều biến thiên của hàm số
f x trên 5π 13π
;
6 6
.
b) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
f x trên π;2π
6
.
c) Tìm m để phương trình
2 2
4 4 16 0f x f x m có nghiệm trên
0;2π.
Câu 2. a) Tìm tập xác định của hàm số
3 2cos
sin 2022
x
yx
.
b) Có bao nhiêu giá trị nguyên dương của tham số m để hàm số
2
5 2 sin 1 cos2y m x m x xác định trên ?
Câu 3. Giải phương trình 2sin 1 0x và cho biết nghiệm của phương trình đã cho được biểu diễn
trên đường tròn lượng giác ở hình bên là những điểm nào?
TRƯỜNG THPT THỦ ĐỨC
4
Câu 4. Giải các phương trình sau
a) tan 1x với 5
2 ; 2
x
b) sin 2 3cos 0x x
c) 3cos20 sin20 2cos21x x x d) 2 2
2sin 4sin cos 4cos 1x x x x
e) 3cos cos2 cos3 1 2sin .sin 2x x x x x f) 2 3sin 3 3 tan 2cos 3x x x .
Câu 5. a) Từ các chữ số 0, 1, 2, 3, 4, 6, 7, 8. Có thể lập được bao nhiêu số chẵn có 4 chữ số khác nhau?
(ĐS: 930)
b) Có bao nhiêu cách chọn 5 cầu thủ từ 11 cầu thủ trong một đội bóng để thực hiện đá 5 quả
luân lưu 11m, theo thứ tự quả thứ nhất đến quả thứ năm. (ĐS: 55440)
c) Có hai chiếc hộp, hộp thứ nhất đựng 3 quả cầu xanh, 5 quả cầu đỏ, hộp thứ hai đựng 4 quả
cầu xanh, 6 quả cầu đỏ. Lấy từ hai hộp 3 quả cầu, trong đó hộp thứ nhất lấy một quả, hộp thứ
hai lấy hai quả. Biết rằng các quả cầu có kích thước khác nhau, hỏi có tất cả bao nhiêu cách sao
cho lấy được cả quả cầu xanh và đỏ? (ĐS: 267)
ĐỀ 04
Câu 1. Cho hàm số
y f x xác định trên và có bảng biến thiên như hình bên duới
a) Hãy mô tả chiều biến thiên của hàm số
f x trên π 9π
;
6 4
.
b) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
f x trên π 7π
;
3 6
.
c) Tìm nghiệm của phương trình
3 2
4 3 0f x f x f x với π 9π
;
3 4
x
.
d) Tìm m để phương trình
f x m có nhiều nghiệm nhất trên π 9π
;
3 4
.
Câu 2. Tìm tập xác định của các hàm số sau
a) 1
2cos 3
x
yx
b) tan 2 5
y x
c) sin 2 1y x
Câu 3. Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau
a) 3sin5 4y x b) 2
sin 6cos 12y x x
Câu 4. a) Tìm m để phương trình sin 3 cos 2
3 3
x x m
vô nghiệm.
TRƯỜNG THPT THỦ ĐỨC
5
b) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sin 2 2cos2 3
2sin 2 cos2 4
x x
yx x
.
Câu 5. Giải các phương trình sau
a)
o
sin 45 1x với o
0 300x b) 2
2sin 5sin 3 0x x
c) 21
cos 2
x d) 3sin 3 cos3 1x x
e) 2 2 2 2
cos cos 2 cos 3 cos 4 2x x x x
f) 2 2 3
4sin 3sin 2 1 2cos
2 2 4
xx x
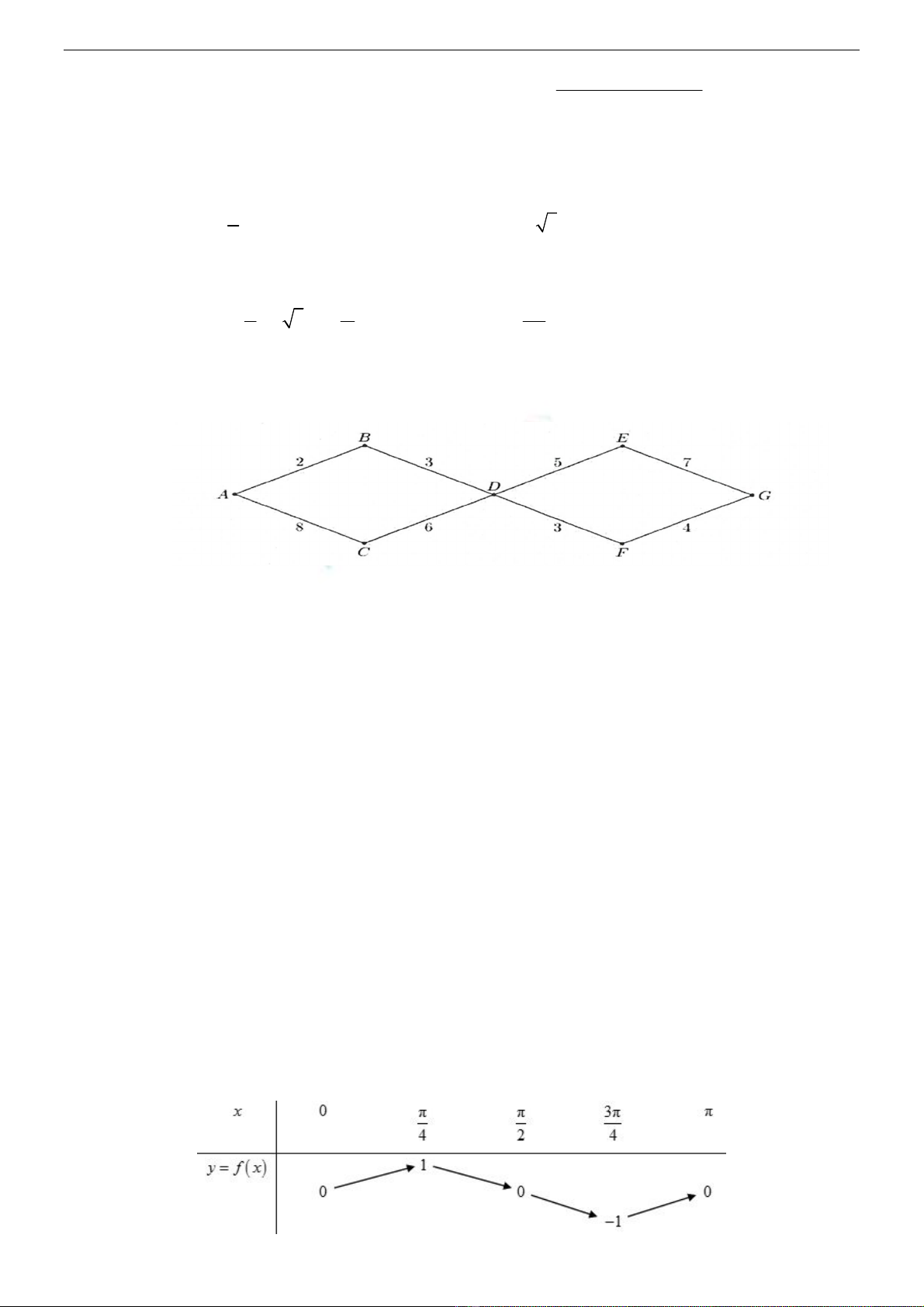
Câu 6. a) Một mạng đường giao thông nối các tỉnh A, B, C, D, E, F và G như hình vẽ bên dưới, trong
đó chữ số 2 viết trên cạnh AB có nghĩa là có 2 con đường nối A và B,…
Hỏi có bao nhiêu cách đi từ A đến G? (ĐS: 2538)
b) Biển số xe máy của tỉnh A (nếu không kể mã số tỉnh) có 6 kí tự, trong đó kí tự ở vị trí đầu
tiên là một chữ cái (trong bảng 26 chữ cái tiếng Anh), kí tự ở vị trí thứ hai là một chữ số thuộc
tập {1;2;…;9}, mỗi kí tự ở bốn vị trí tiếp theo là một chữ số thuộc tập {0;1;2;…;9}. Hỏi nếu
chỉ dùng một mã số tỉnh thì tỉnh A có thể làm được nhiều nhất bao nhiêu biển số xe máy khác
nhau? (ĐS: 2340000)
c) Số 253125000 có bao nhiêu ước số tự nhiên? (ĐS: 180)
d) Từ các chữ số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số lẻ gồm 4 chữ số khác nhau (ĐS:
144)
Câu 7. Một đoàn tàu có 3 toa chở khách. Toa I, II, III. Trên sân ga có 4 khách chuẩn bị đi tàu. Biết mỗi
toa có ít nhất 4 chỗ trống. Hỏi
a) Có bao nhiêu cách sắp xếp cho 4 vị khách lên 3 toa? (ĐS: 81)
b) Có bao nhiêu cách sắp xếp cho 4 vị khách lên tàu có 1 toa có 3 trong 4 vị khách nói trên?
ĐỀ 05
Câu 1. Cho hàm số
y f x có bảng biến thiên như hình bên duới