SỞ GD&ĐT QUẢNG TRỊ
TRƯỜNG PHỔ THÔNG DTNT TỈNH
ĐỀ KIỂM TRA CHÍNH THỨC
(Đề có 5 trang)
ĐỀ KIỂM TRA GIỮA KỲ 1- NĂM HỌC 2024- 2025
MÔN TOÁN 12
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
Mã đề thi: 211
Họ và tên học sinh: .................................................................Lớp :...................................
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
hỏi thí sinh chỉ chọn một phương án.
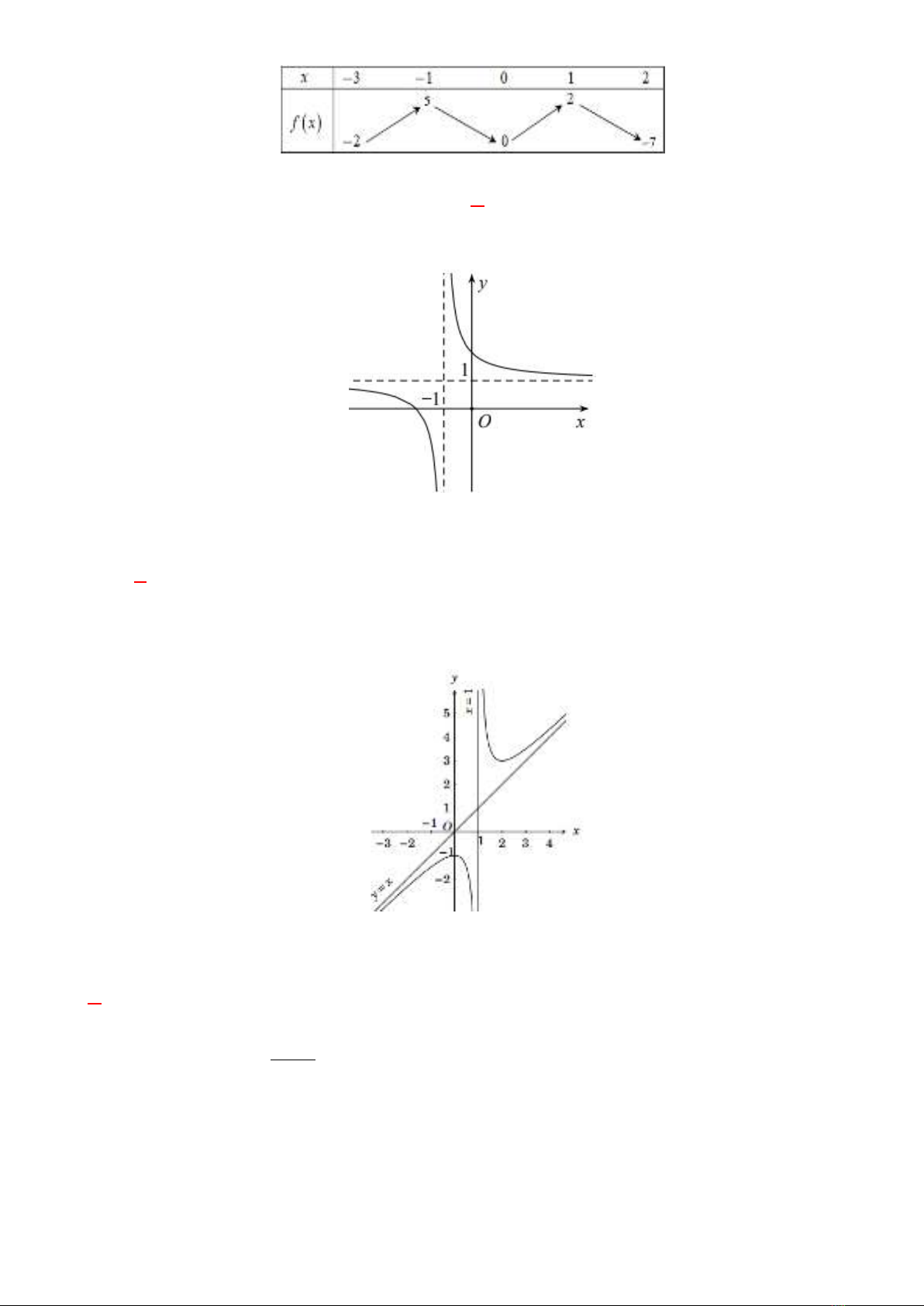
Câu 1: Cho hàm số
()fx
có bảng xét dấu đạo hàm
'( )fx
như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
( ;0).
B.
(0; ).
C.
( 2;0).
D.
(0;2).
Câu 2: Cho hàm số
có đồ thị như hình vẽ sau.
Giá trị cực đại của hàm số đã cho bằng
A.
1.
B.
3.
C.
2.
D.
1.
Câu 3: Cho hàm số
có đồ thị như hình vẽ sau.
Số điểm cực tiểu của hàm số đã cho là
A.
2.
B.
3.
C.
0.
D.
1.
Câu 4: Cho hàm số
liên tục trên đoạn
[ 1;3]
và có đồ thị như hình vẽ sau.
1
2
3
1
2
3
4
x
y
O
2
1
Giá trị nhỏ nhất của hàm số đã cho trên đoạn
1;3
là
A.
2.
B.
3.
C.
4.
D.
1.
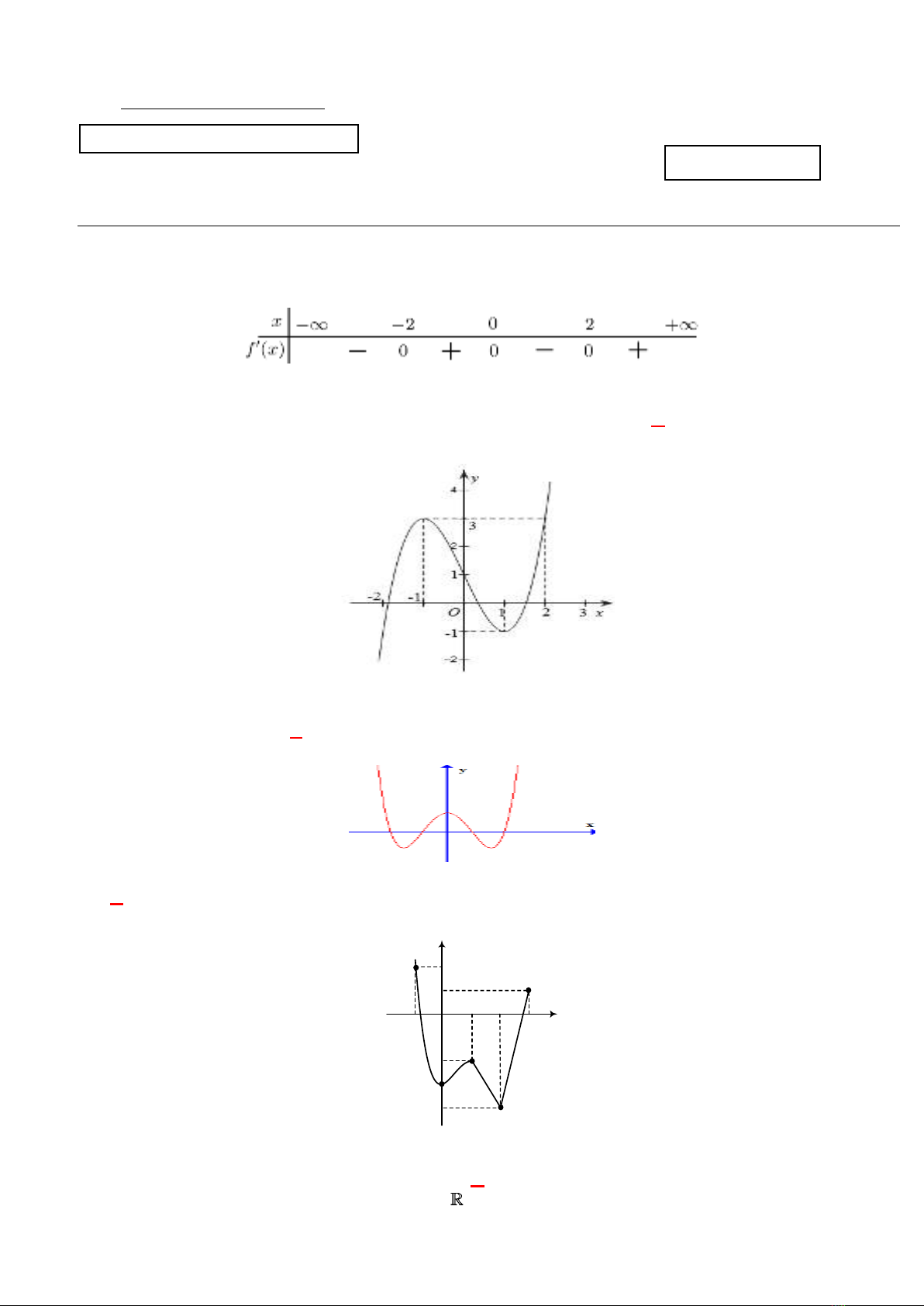
Câu 5: Cho hàm số
liên tục trên đoạn và có bảng biến thiên như sau.
Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn
3;1
.Tính
.Mm
A.
2.
B.
4.
C.
3.
D.
2.
Câu 6. Cho hàm số
y f x
có đồ thị như hình vẽ bên dưới.
Phát biểu nào sau đây là đúng?
A. Đồ thị hàm số có đường tiệm cận đứng
1x
, đường tiệm cận ngang
0y
.
B. Đồ thị hàm số có đường tiệm cận đứng
1x
, đường tiệm cận ngang
1y
.
C. Đồ thị hàm số có đường tiệm cận đứng
0x
, đường tiệm cận ngang
0y
.
D. Đồ thị hàm số có đường tiệm cận đứng
0x
, đường tiệm cận ngang
1y
.
Câu 7. Cho hàm số
y f x
có đồ thị như hình vẽ bên dưới.
Khẳng định nào sau đây đúng?
A. Đồ thị hàm số có tiệm cận đứng là đường thẳng
1x
và tiệm cận ngang là đường thẳng
1.y
B. Đồ thị hàm số có tiệm cận đứng là đường thẳng
1x
và tiệm cận xiên là đường thẳng
.yx
C. Đồ thị hàm số có tiệm cận đứng là đường thẳng
1x
và tiệm cận xiên là đường thẳng
.yx
D. Đồ thị hàm số có tiệm cận đứng là đường thẳng
0x
và tiệm cận xiên là đường thẳng
.yx
Câu 8. Cho hàm số
xa
ybx c
;
( , , ; 0)a b c Z c ab
có đồ thị là đường cong như hình vẽ
Khẳng định nào sau đây đúng?
A. Đồ thị hàm số đối xứng qua đường thẳng
1.x
B. Đồ thị hàm số đối xứng qua đường thẳng
1.y
C. Đồ thị hàm số có tâm đối xứng là điểm
(1;1).I
D. Đồ thị hàm số không có tâm đối xứng.
Câu 9: Hàm số
33y x x
đồng biến trên khoảng nào dưới đây?
A.
1;1
. B.
;1
. C.
1;
. D.
0; 3
.
Câu 10: Hàm số
32
31f x x x
đạt giá trị lớn nhất trên
1;4
tại điểm
A.
1x
. B.
2x
. C.
3
2
x
. D.
3x
.
Câu 11: Đường thẳng
1x
là tiệm cận đứng của hàm số nào sau đây?
A.
2
2
32
1
xx
yx

. B.
232
1
xx
yx

. C.
2
1
43
x
yxx
. D.
2
1
1
x
yx
.
Câu 12: Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào dưới đây?
A.
21y x x
. B.
331y x x
. C.
32
31y x x
. D.
331y x x
.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở
mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số
y f x
liên tục trên và có bảng biến thiên như sau:
Khi đó:
a) Hàm số đã cho đồng biến trên khoảng
1;
.
b) Giá trị lớn nhất của hàm số trên đoạn
11[ ; ]
bằng 4.
c) Điểm cực tiểu của đồ thị hàm số là
01( ; ).
d) Hàm số có
2
điểm cực trị.
Câu 2. Cho hàm số bậc ba
y f x
có đồ thị là đường cong như trong hình dưới đây.
a) Hàm số đã cho nghịch biến trên khoảng
1( ; ).
b) Giá trị lớn nhất của hàm số trên đoạn
13[ ; ]
bằng 2.
c) Giá trị nhỏ nhất của hàm số trên đoạn
13[ ; ]
bằng
4.
d) Hàm số đồng biến trên khoảng
42;
.
Câu 3. Cho hàm số
21
1
x
yx
.
a) Đồ thị hàm số có đường tiệm cận đứng là
1.x
b) Hàm số đã cho không có cực trị.
c) Hàm số nghịch biến trên khoảng
1;
và đồng biến trên khoảng
1( ; )
.
d) Hàm số có đồ thị là đường cong trong hình bên dưới
Câu 4. Cho hàm số
2
21
1
xx
yx
có đồ thị
.C
a) Đồ thị hàm số có đường tiệm cận đứng là
1 .x
b) Đồ thị hàm số có đường tiệm cận xiên
21 .yx
c) Hàm số đồng biến trên khoảng
20;
.
d) Hàm số có bảng biến thiên là
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Cho hàm số
32
31y x x
có đồ thị là
.C
Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ
nhất của hàm số trên đoạn
[ 1;3].
Tính giá trị
4.P M m
A. 13
Lời giải
2
' 3 6 ; ' 0 0; 2.y x x y x x
( 1) 3; (0) 1; (2) 3; (3) 1.f f f f
1; 3 4 1 4( 3) 13.M m P M m
13.P
Câu 2. Cho hàm số
xa
ybx c
với
0; 0,b c ab
có đồ thị như hình vẽ dưới đây:
Tính giá trị biểu thức
2 3 4 .T a b c
A. -11
Lời giải
Dựa vào đồ thị ta có
TCN
1
1 1 1.yb
b
TCĐ
1 1 1.
c
x c b c
b
Đồ thị đi qua điểm
(0;2)
, Nên ta có
2 2 2.
1
aaa
c
Vậy
2; 1; 1 2 3 4 4 3 4 11.a b c T a b c
Câu 3: Cho hàm số
32
34y x x
có đồ thị
( ).C
Phương trình tiếp tuyến của đồ thị
()C
tại điểm
(3;4)M
có dạng
.y ax b
Tính giá trị
..S a b
C. -207
Lời giải
Hệ số góc
'(3) 9.kf
Phương trình tiếp tuyến tại M là:
4 9( 3) 9 23 9; 23.y x y x a b
. 9.( 23) 207.S a b
Câu 4: Người ta thống kê được chi phí sửa chữa, vận hành máy móc trong một năm của xưởng sản xuất
được tính bởi công thức
2025 150
() 32 3
x
fx x
(triệu đồng). Biết x là số năm kể từ lúc máy móc vận hành
lần đầu tiên, số năm càng nhiều thì chi phí càng cao. Khi số năm x đủ lớn thì chi phí vận hành máy móc
trong một năm gần với số nào ? (làm tròn kết quả đến hàng phần chục).
A. 63,3
Lời giải
Chi phí vận hành máy trong một năm khi số năm x đủ lớn là
2025 150 2025
lim ( ) lim 63,3.
32 3 32
xx
x
fx x
 
Câu 5: Cắt một đoạn dây dài
60m
thành hai đoạn dây, đoạn dây thứ nhất gấp thành một tam giác đều
có diện tích
1
S
, đoạn dây thứ hai gấp thành một hình vuông có diện tích
2
S
(như hình vẽ dưới)