TRƯỜNG THPT DĨ AN KIỂM TRA GIỮA HỌC KỲ 1 NĂM HỌC 2021 – 2022
TỔ TOÁN Môn: TOÁN
Lớp: 12
(Đề thi gồm có 05 trang) Thời gian: 60 phút, không kể thời gian giao đề
(100% Trắc nghiệm 32 câu)
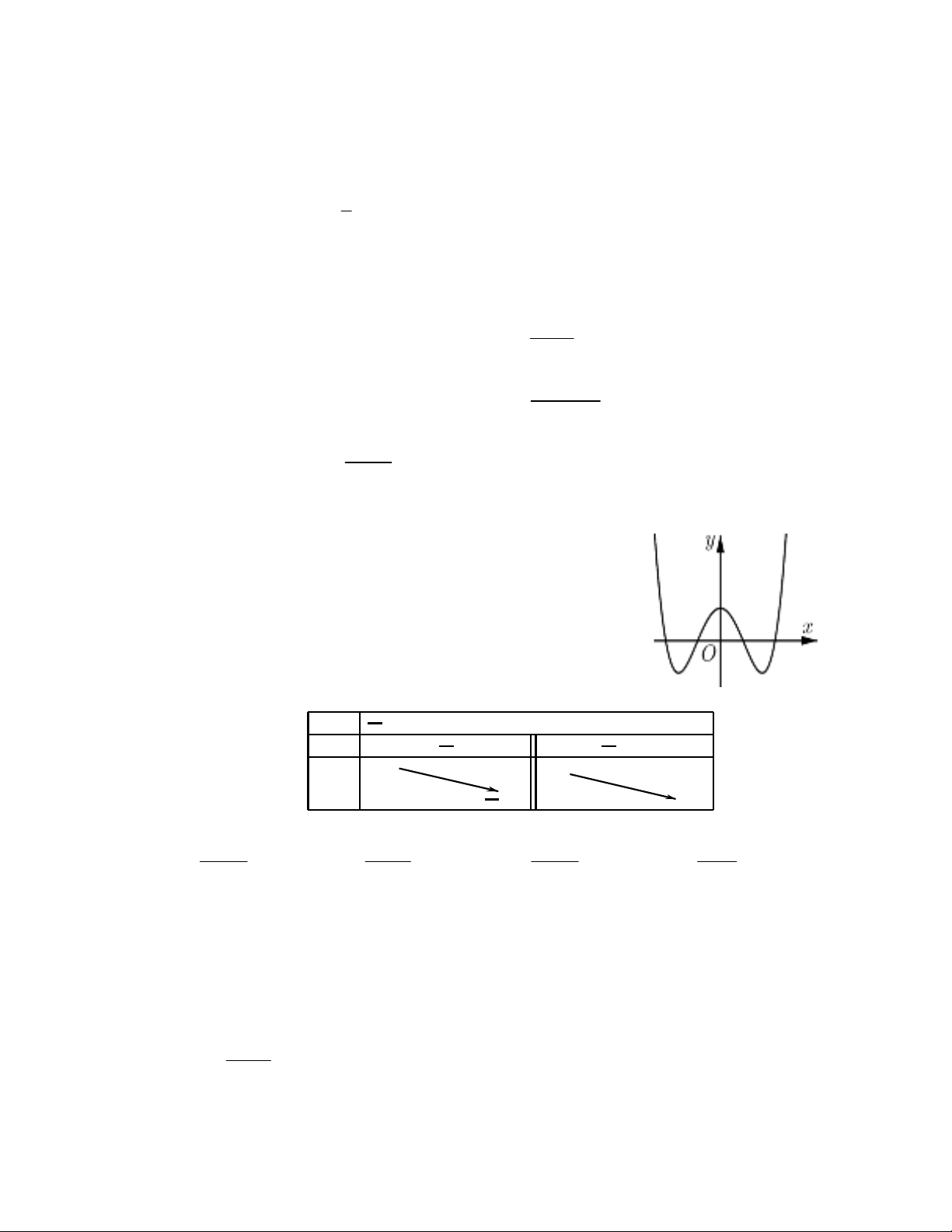
Câu 1. Cho hàm số
y f x
có đồ thị như hình vẽ bên.
Hàm số đã cho đồng biến trong khoảng nào dưới đây ?
A.
1;
. B.
0;1
.
C.
3;1
. D.
2;0
.
Câu 2. Hàm số
4 2
8 6y x x
đồng biến trên khoảng nào dưới đây?
A.
2;0
và
2;
. B.
; 2
và
2;
.
C.
2;2
. D.
; 2
và
0;2
.
Câu 3. Hàm số nào sau đây nghịch biến trên
1;3
?
A.
3 2
12 3 1
3
y x x x
. B.
1
2
x
yx
.
C.
2
2 1
2
x x
yx
. D.
2
1y x
.
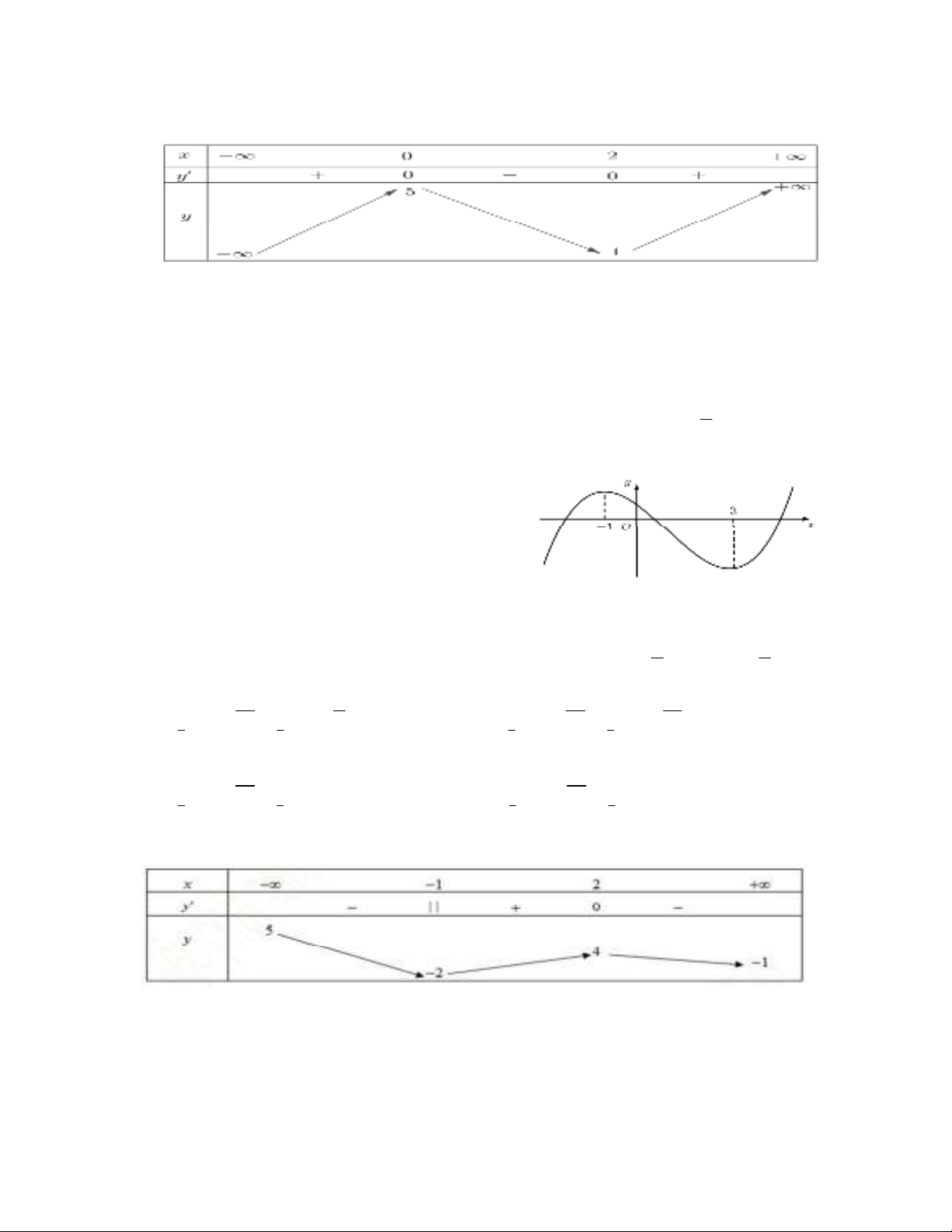
Câu 4. Cho hàm số
y f x
có bảng biến thiên như hình sau:
Hàm số
( ) 1 2x 1g x f
đồng biến trên khoảng
A.
1;1
2
. B.
3
0; 2
. C.
1;
. D.
1
1; 2
.
Câu 5. Hàm số
242
3
1
23
xxxy
có bao nhiêu điểm cực trị ?
A. 0. B. 1. C. 2. D. 3.
x
y
1
1
3
O
Câu 6. Cho hàm số
y f x
có bảng biến thiên như hình vẽ. Kết luận nào sau đây là
đúng?
A. Hàm số đạt cực tiểu tại
1x
.
B. Hàm số có hai điểm cực đại
.
C. Hàm số đạt cực đại tại
0x
.
D. Hàm số đồng biến trên khoảng
1;
.
Câu 7. Tìm tất cả các giá trị của tham số m sao cho đồ thị hàm số
4 2 4
2 2y x mx m m
có ba điểm cực trị đều thuộc các trục toạ độ.
A.
1m
. B.
2m
. C.
1
0
m
m
. D.
1
2
m
.
Câu 8. Cho hàm số bậc ba
y f x
có đồ thị
như hình vẽ bên. Gọi
S
là tập hợp tất cả các
giá trị nguyên của tham số m để hàm số
2
( ) 1g x f x m
có
3
điểm cực trị. Tổng
các phần tử của
S
là:
A.
2
. B.
4
. C.
8
. D.
10
.
Câu 9. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1
y x x
trên đoạn
3;3
2
.
A.
3;3
2
10
max 3
y
, 3;3
2
5
min 2
y
. B.
3;3
2
10
max 3
y
, 3;3
2
13
min 6
y
.
C.
3;3
2
10
max 3
y
,
3;3
2
min 2y
. D. 3;3
2
16
max 3
y
,
3;3
2
min 2y
.
Câu 10. Cho hàm số
y f x
liên tục trên
và có bảng biến thiên
Khẳng định nào sau đây sai ?
A. Hàm số có hai điểm cực trị.
B. Đồ thị hàm số có hai tiệm cận ngang.
C. Hàm số có giá trị lớn nhất bằng
5
và giá trị nhỏ nhất bằng
2
.
D. Hàm số không có giá trị lớn nhất và có giá trị nhỏ nhất bằng
2
.
Câu 11. Trên khoảng
0;
thì hàm số
3
3 1y x x
A. có giá trị nhỏ nhất là 3. B. có giá trị lớn nhất là 1.
C. có giá trị nhỏ nhất là 1. D. có giá trị lớn nhất là 3.
Câu 12. Cho hàm số
3 2
1
3
y x x x m
với m là tham số. Biết
3;0
min 2y
, giá trị của
m là:
A.
23
. B.
2
. C.
19
. D.
2
.
Câu 13. Đồ thị của hàm số nào dưới đây có tiệm cận ngang ?
A.
4 2
y x x
. B.
3 1
1
x
yx
.
C.
3 2
3 3 1y x x x
. D.
2
1
1
x x
yx
.
Câu 14. Đồ thị hàm số
2
2
4
x
yx
có bao nhiêu tiệm cận ?
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 15. Đường cong hình bên là đồ thị của một trong các hàm số
sau, hỏi đó là hàm số nào?
A.
4 2
3 1y x x
. B.
3 2
3 1y x x
.
C.
4 2
3 1y x x
. D.
4 2
3 1y x x
.
Câu 16. Bảng biến thiên sau đây là của hàm số nào?
A.
2 5
2
x
yx
. B.
2 1
2
x
yx
. C.
2 3
2
x
yx
. D.
3
2
x
yx
.
Câu 17. Cho hàm số
3
3 2y x x
có đồ thị
C
. Viết phương trình tiếp tuyến của
C
tại giao điểm của
C
với trục tung.
A. 2 1y x . B. 2 1y x . C. 3 2y x . D. 3 2y x .
Câu 18. Gọi
,M
N là giao điểm của đường thẳng
: 1d y x
và đường cong
2 1
:5
x
C y x
. Hoành độ trung điểm
I
của đoạn thẳng MN bằng:
A.
2
. B.
2
. C.
1
. D.
1
.
2
2
∞
+∞
2
∞+∞
y
y'
x
Câu 19. Cho hàm số bậc ba
y f x
có đồ thị như hình
bên. Phương trình
2
1 0f x
có bao nhiêu nghiệm?
A.
4
. B.
0
.
C.
2
. D.
3
.
Câu 20. Cho đồ thị của hàm số
4 2
f x ax bx c
như hình vẽ sau. Khẳng định nào sau
đây là đúng?
A.
2
0; 0; 0; 4 0a b c b ac
.
B.
2
0; 0; 0; 4 0a b c b ac
.
C.
2
0; 0; 0; 4 0a b c b ac
.
D.
2
0; 0; 0; 4 0a b c b ac
.
Câu 21. Biết đồ thị hàm số bậc ba
3 2
y f x ax bx cx d
có hai điểm cực trị
1;3A
,
3; 1B
. Tính giá trị
2f
.
A.
2 1f
. B.
2 1f
. C.
2 2f
. D.
2 0f
.
Câu 22. Cho hàm số
y f x
có đạo hàm liên
tục trên
. Đồ thị
y f x
như hình vẽ bên.
Số đường tiệm cận đứng của đồ thị hàm số
2
2
2x x
yf x f x
là:
A.
3
. B.
4
.
C.
2
. D.
5
.
Câu 23. Mặt phẳng
'A BC
chia khối lăng trụ
. ' ' 'ABC A B C
thành các khối đa diện nào?
A. Ba khối tứ diện.
B. Hai khối chóp tứ giác.
C. Hai khối chóp tam giác.
D. Một khối chóp tam giác và một khối chóp tứ giác.
Câu 24. Số mặt phẳng đối xứng của hình lập phương ?
A. 6. B. 8. C. 7. D. 9.
Câu 25. Khối đa diện đều loại
3;4
là khối:
A. Hai mươi mặt đều. B. Bát diện đều.
C. Lập phương. D. Mười hai mặt đều.
y
O
Câu 26. Khối đa diện đều nào sau đây có mặt không phải là tam giác đều?
A. Khối hai mươi mặt đều. B. Khối bát diện đều.
C. Khối tứ diện đều. D. Khối lập phương.
Câu 27. Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
,
a
góc giữa cạnh bên và
mặt phẳng đáy bằng
60
. Tính thể tích khối chóp
.
S ABCD
.
A.
3
6
2
a
. B.
3
6
6
a
. C.
3
6
a
. D.
3
6
3
a
.
Câu 28. Khối lăng trụ có thể tích bằng
,
V
diện tích mặt đáy bằng
S
. Chiều cao của khối
lăng trụ bằng:
A.
S
V
. B.
3
V
S
. C.
V
S
. D.
3
S
V
.
Câu 29. Cho khối lăng trụ
. ' ' '
ABC A B C
có thể tích bằng
.
V
Tính thể tích khối đa diện
' ' .
BAA C C
A.
3
4
V
. B.
2
3
V
. C.
2
V
. D.
4
V
.
Câu 30. Độ dài đường chéo một mặt của hình lập phương là
2
a
. Tính thể tích
V
của
khối lập phương.
A.
3
V a
. B.
3
8
V a
. C.
3
3 3
V a
. D.
3
3
V a.
Câu 31. Cho hình lập phương
. ' ' ' '
ABCD A B C D
cạnh bằng
1
. Gọi
M
là trung điểm cạnh
'
BB
. Mặt phẳng
( ' )
MA D
cắt cạnh
BC
tại
K
. Thể tích khối đa diện lồi
' ' ' '
A B C D MKCD
là:
A.
7
24
. B.
7
17
. C.
17
24
. D.
1
24
.
Câu 32. Cho
hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA SB
,
SC SD
,
SAB SCD
và tổng diện tích hai tam giác
SAB
và
SCD
bằng
2
7
10
a
.
Tính thể tích
V
của khối chóp
.
S ABCD
.
A.
3
4
15
a
V
. B.
3
4
25
a
V
. C.
3
12
25
a
V
. D.
3
2 3
15
a
V
.
----------Hết----------