1
TRƯỜNG TH – THCS THẮNG LỢI KHUNG MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ I
TỔ: TOÁN – KHTN Năm học : 2024 – 2025
MÔN: TOÁN - LỚP: 8
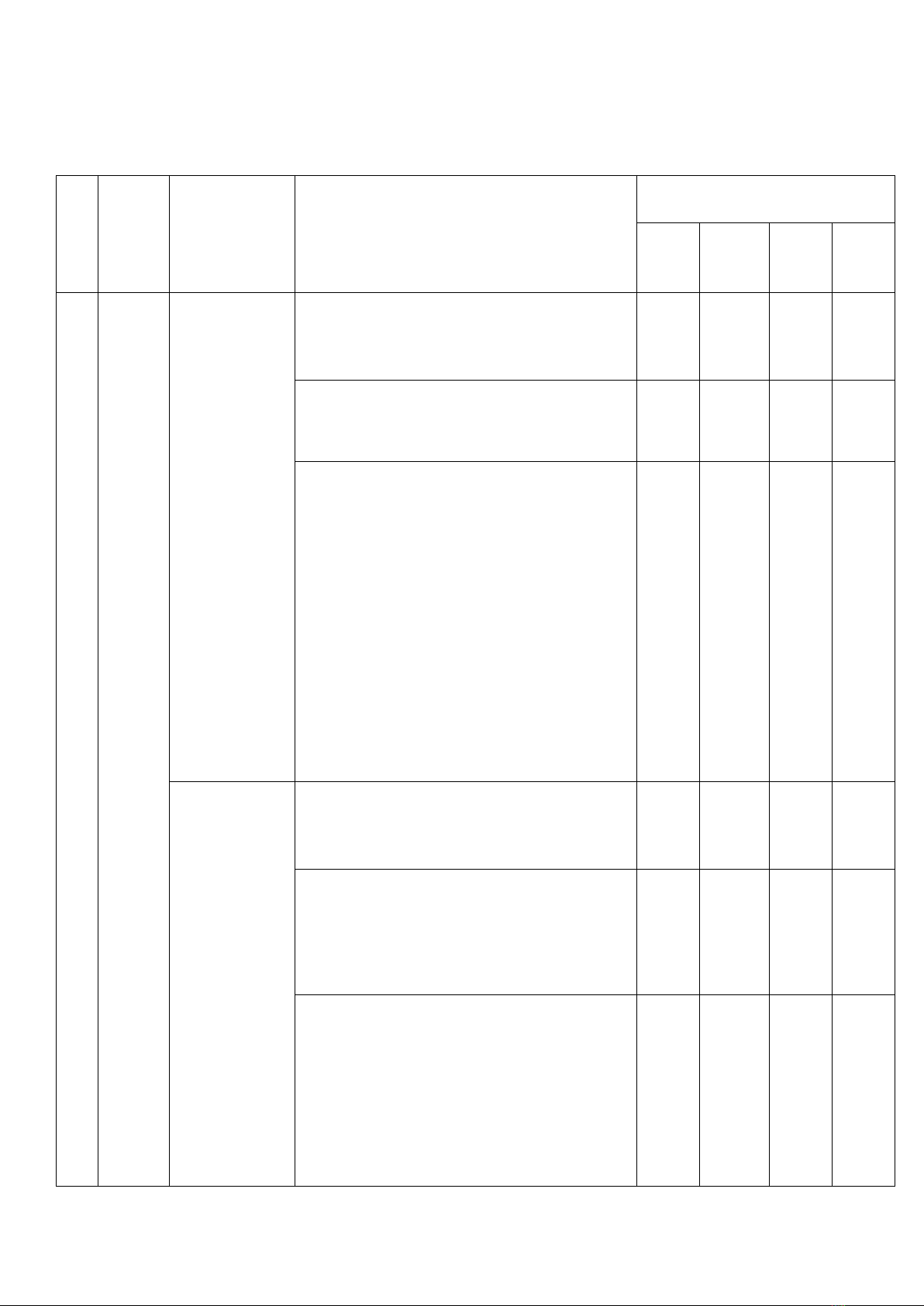
TT
(1)
Chương/
Chủ đề
(2)
Nội dung / đơn vị kiến thức
(3)
Mức độ đánh giá
Tng
%
điểm
(12)
Nhn biết
Thông hiểu
Vn dng
Vn dng
cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
1
Biểu thức
đại số
Đa thức nhiều biến. Các
phép toán cộng, trừ,
nhân, chia các đa thức
nhiều biến.
5
1
1
25%
2,5đ
Hằng đẳng thức đáng
nhớ.
5
1
1
25%
2,5đ
2
Các hinh
khối
trong
thực tiễn
Hinh chp tam giác đều,
hnh chp tứ giác đều.
2
2
1
20,0
%
2,0đ
3
Định lí
Pythagor
e
Định lí Pythagore.
1
10,0%
1,0đ
4
Tứ giác
Tứ giác.
2
3,0%
0,5đ
Tính chất và dấu hiệu
nhận biết các tứ giác đặc
biệt
2
1
15,0%
1,5đ
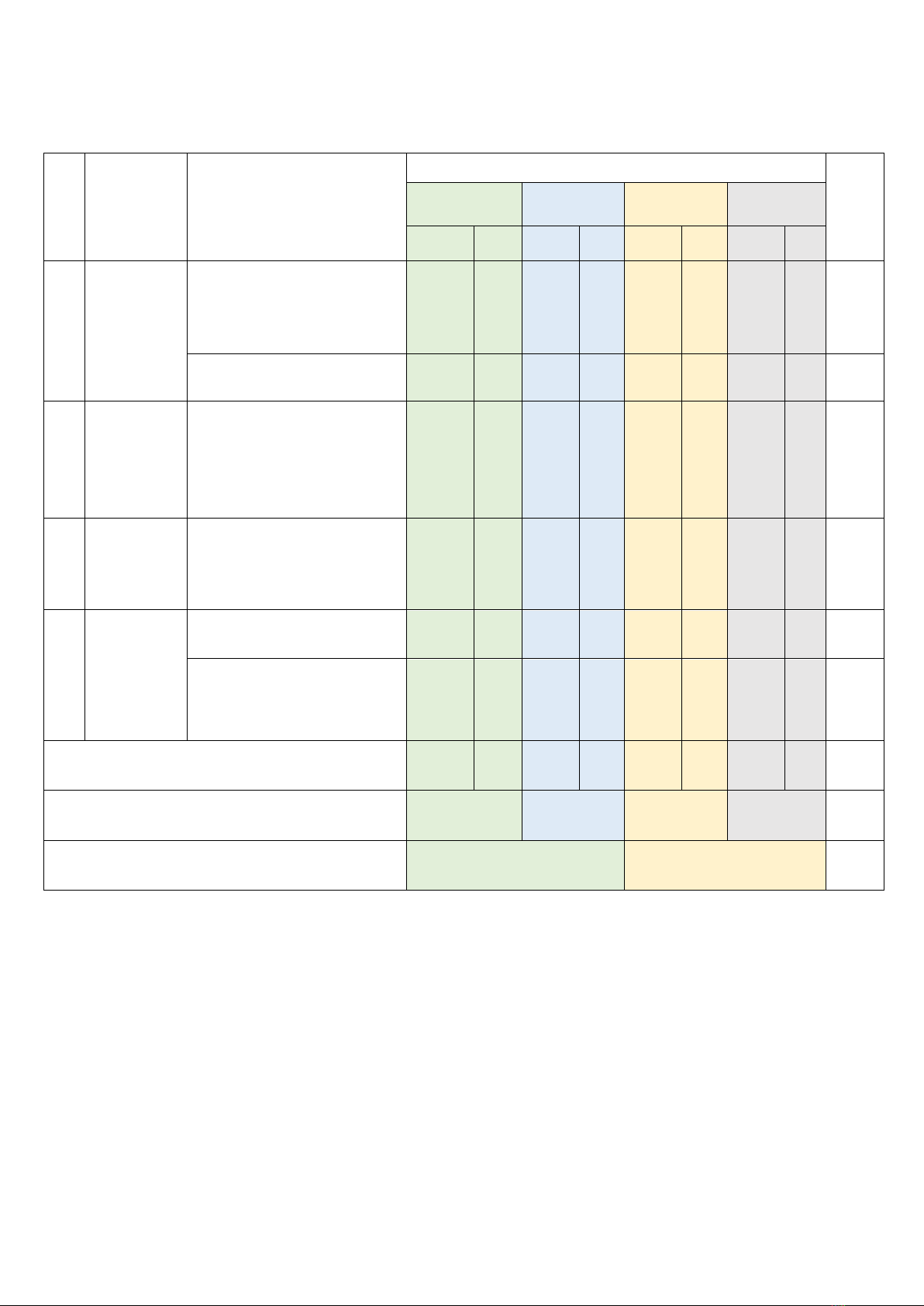
Tổng
33 tiết
16
4đ
4
1đ
1
2đ
2
2đ
1
1đ
25
10,0đ
Tỉ lệ %
40%
30%
20%
10%
100
%
Tỉ lệ chung
70%
30%
100
%