PHÒNG GD & ĐT TP KON TUM
MA TRẬN ĐỀ KIỂM TRA GIỮA HC KÌ I
TRƯỜNG TH-THCS ĐĂK RƠ WA
NĂM HC 2024 - 2025
MÔN TOÁN 9
Thời gian: 90 phút (không kể thời gian phát đề)
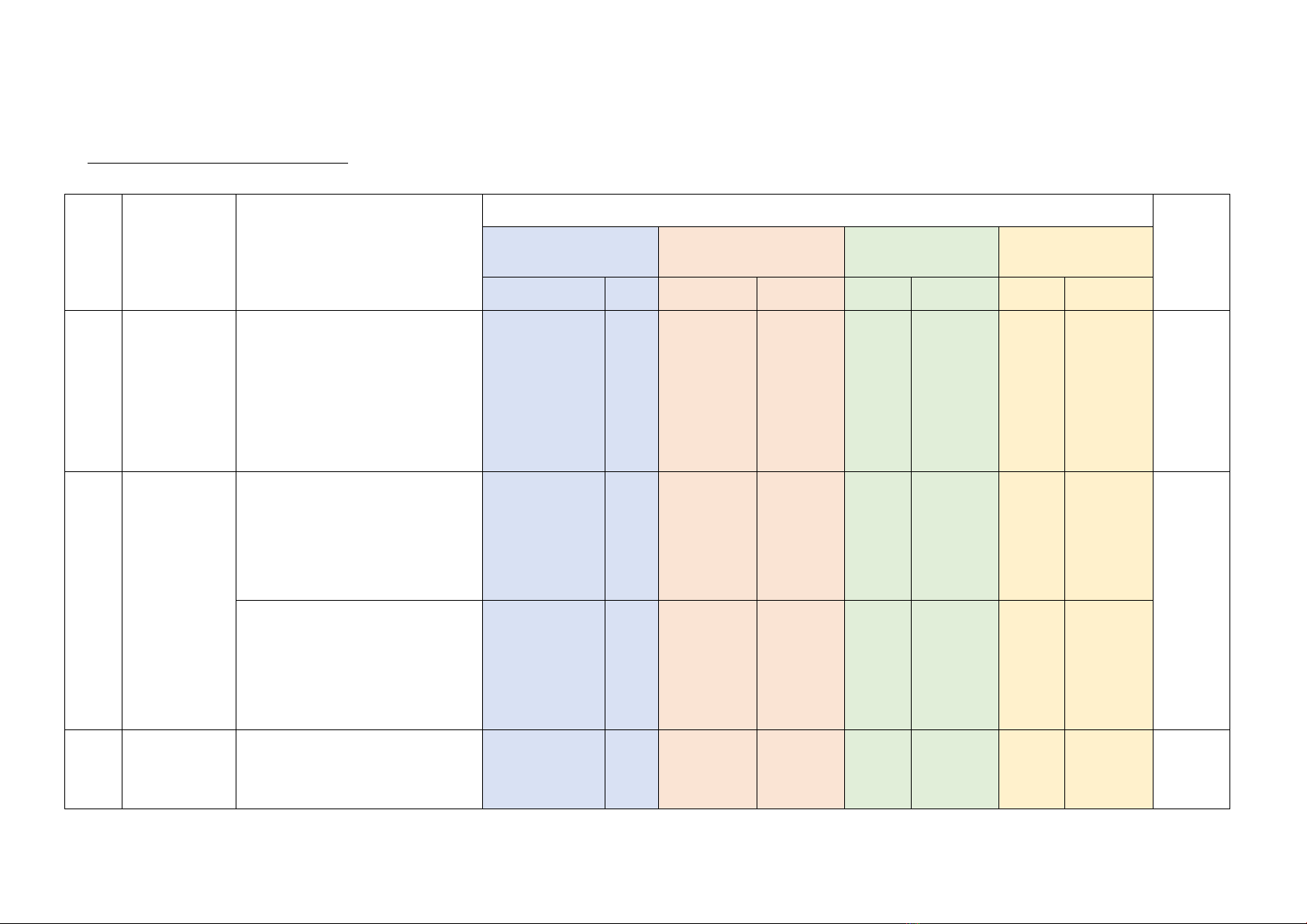
STT
Chương/
Chủ đề
Nội dung/ đơn vị kiến thức
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá
Tổng
%
điểm
Nhận biết
Thông hiểu
Vận dụng
Vận dụng cao
TN
TL
TN
TL
TN
TL
TN
TL
1
Phương trình
và hệ hai
phương trình
bậc
nhất hai ẩn
(12 tiết)
Khái niệm phương trình và hệ hai
phương trình bậc nhất hai ẩn. Giải
hệ hai phương trình bậc nhất hai
ẩn. Giải bài toán
bằng cách lập hệ phương trình
6
(C1,4,5,7,15,20)
(1,5đ)
4
(C2,11,13,14)
(1,0đ)
1
(C2)
(1,0đ)
35%
2
Phương
trình và bất
phương
trình bậc nhất
một ẩn
(7 tiết)
Phương trình quy về phương trình
bậc nhất một ẩn
2
(C16,17)
(0,5đ)
1
(C1a)
(1,0đ)
1
(C1b)
(1,0đ)
30%
Bất đẳng thức
2
(C6,8)
(0,5đ)
3
Hệ thức
Tỉ số lượng giác của góc nhọn.
6
(C3,9,10,12,18,
19)
(1,5đ)
35%








































