PHÒNG GD-ĐT TP. NAM ĐỊNH
TRƯỜNG THCS PHÙNG CHÍ KIÊN ĐỀ KIỂM TRA CHẤT LƯỢNG GIỮA HỌC KÌ II
NĂM HỌC 2022-2023- MÔN TOÁN LỚP 9
Thời gian: 90 phút (không kể thời gian giao đề)
Phần I: Trắc nghiệm (2,0 điểm): Hãy chọn đáp án đúng và ghi vào bài làm
Câu 1. Điểm nào sau đây thuộc đồ thị hàm số
2
2
x
y=
?
A.
1
( 1; )
2
−
; B.
( 2; 2)− −
; C.
( 3;3)−
; D.
1 1
( ; )
2 2
−
.
Câu 2. Giá trị nào của m thì phương trình x2 – (m+1)x + m -1= 0 có nghiệm là -2 ?
A. m =
9
5
B. m = 2 C. m =
3
5
D. m = -2
Câu 3. Trong các hàm số sau, hàm số nào nghịch biến khi x > 0.
A. y = x B.
2
y 2.x=
C. y = 2x + 3 D.
( )
2
y 3 2 x= −
Câu 4. Phương trình x2 + 3x + 1 = 0 có biệt thức ∆ bằng
A. -3 B. 3 C. 6 D. 5
Câu 5. Cho hai đường tròn (O;2cm); (O’;5cm) và OO’= 3cm. Hai đường tròn này có vị trí
A. tiếp xúc ngoài B. ở ngoài nhau C. tiếp xúc trong D. cắt nhau
Câu 6. Cho đường tròn (O) và điểm M nằm ngoài đường tròn. MA và MB là các tiếp tuyến
tại A và B. Số đo của góc AMB bằng 720. Số đo của góc OAB bằng
A. 450 B. 540 C. 360 D. 720
Câu 7: Trong các hình sau, hình nào nội tiếp được trong một đường tròn?
A.. Hình thang B. Hình thang cân C. Hình thoi. D. Hình bình hành
Câu 8: Cho đường tròn (O; R) ngoại tiếp tam giác ABC vuông cân ở A. Khi đó AC bằng:
A. R B. 2R C.2
2
R D. R
2
Phần II: Tự luận (8,0 điểm)
Bài 1( 1,5 điểm): Giải phương trình và hệ phương trình:
a) 2x2 – 4x – 3 = 0. b)
Bài 2 ( 1,5 điểm): Cho M =
x 1 1 2
- : + x - 1
x - 1 x - x x 1
+
với
x 0, x 1
>
.
a) Rút gọn biểu thức M.
b) Tìm x sao cho M > 0.
Bài 3 (1,25 điểm): Cho hàm số y =
2
x
3
−
có đồ thị là (P) và đường thẳng (d): y = 2x+k
a) Tìm k biết rằng đường thẳng (d) đi qua điểm B( -2: -1) ?
b)Tìm tọa độ điểm chung của đường thẳng (d) và Parabol (P) với k vừa tìm được ở câu a?
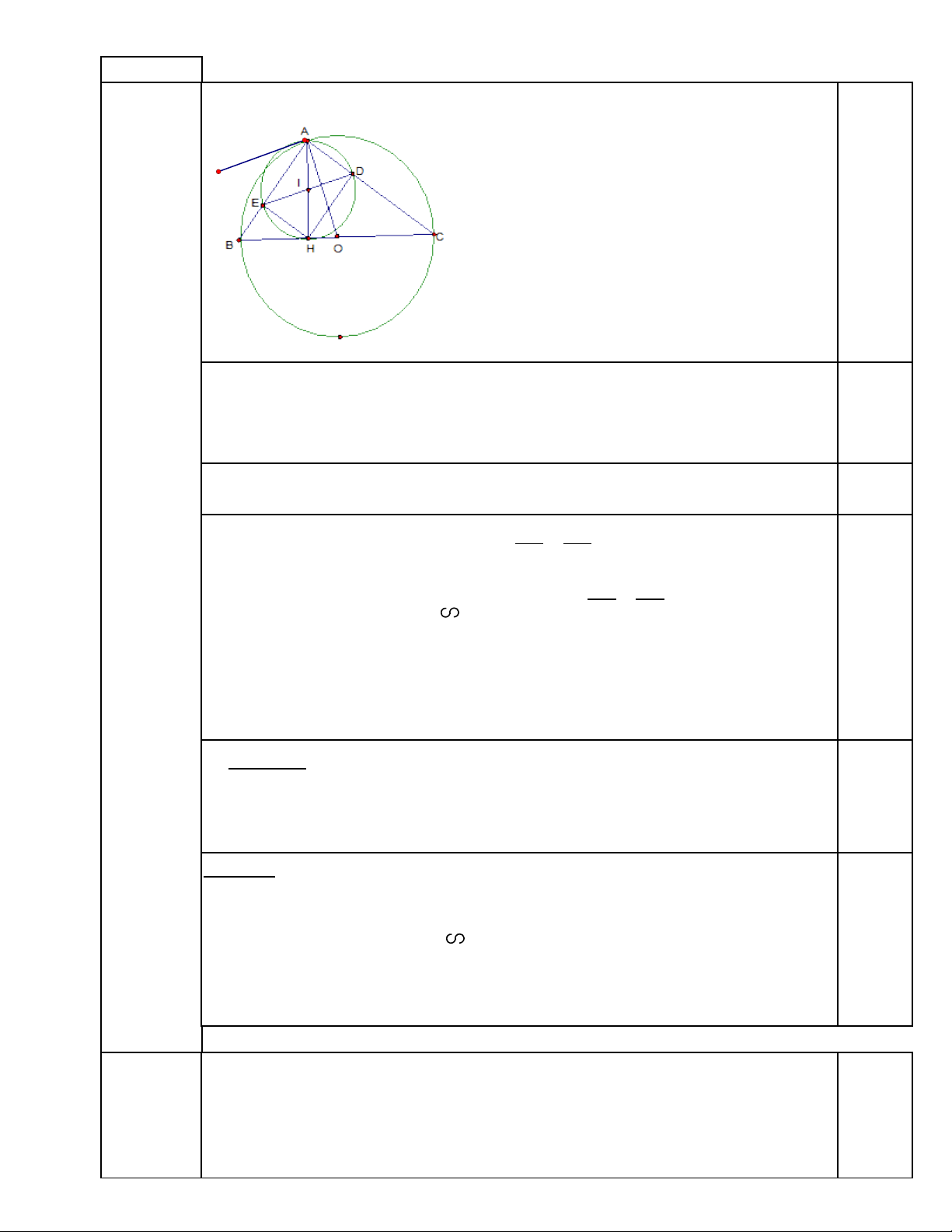
Bài 4 ( 3,0 điểm): Cho đường tròn (O;R) đường kính BC. Lấy điểm A trên đường tròn
(O;R) sao cho AC > AB. Vẽ AH vuông góc với BC tại H. Vẽ đường tròn (I) đường kính AH
cắt AB và AC lần lượt tại E và D. Chứng minh :
1) Tứ giác ADHE là hình chữ nhật
2) AE. AB = AD. AC
3) Tứ giác BCDE nội tiếp và OA vuông góc với DE
Bài 5 (0,75 điểm): Hai số thực x, y thoả mãn:
3 2
2 2 2
x 2y 4y 3 0
x x y 2y 0
+ − + =
+ − =
.
Tính giá trị biểu thức P =
2 2
x y+
.
……………………….HẾT……………………….
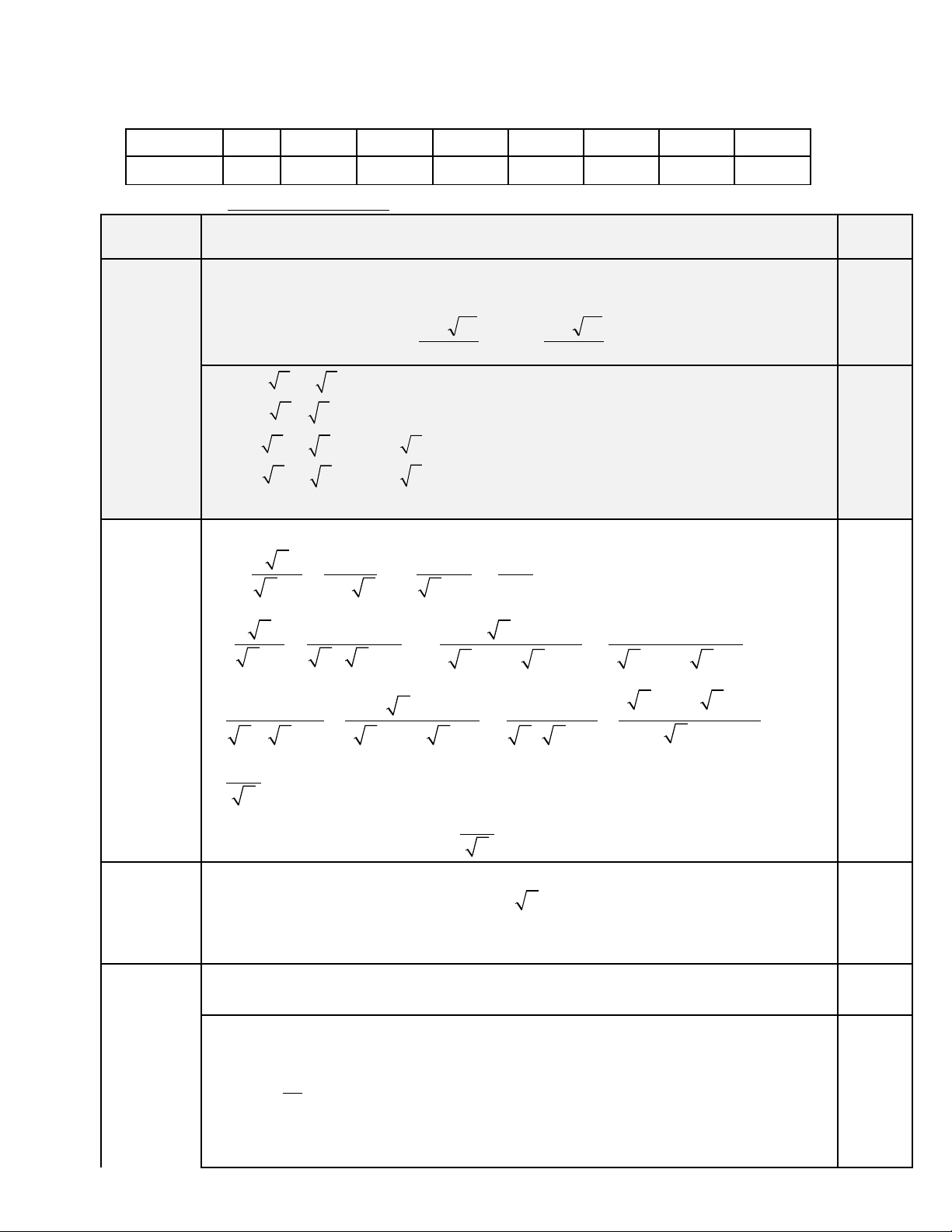
HƯỚNG DẪN VÀ BIỂU ĐIỂM CHẤM
Phần I: Trắc nghiệm( 2 điểm): Mỗi câu đúng được 0,25 điểm
Câu 1 2 3 4 5 6 7 8
Đáp án A C D D C C B D
Phần II:Tự luận ( 8,0 điểm)
BÀI NỘI DUNG ĐIỂM
Bài1
(1,5 đ)
a) Phương trình: 2x2 – 4x – 3 = 0
Tính được
10)3.(2)2( 2'
Suy ra được :
2
102
1
x
;
2
102
1
x
0,25
0, 5
b)
3 x 2 y 1
2 x y 4
− = −
+ =
ÐK : x 0;y 0
3 x 2 y 1 x 1 x 1
y 4
y 2
4 x 2 y 8
− = − ==
=
=
+ =
(TMĐK)
Vậy:
0, 5
0,25
Bài 2
( 1,5
điểm)
a) Với x> 0; x≠1, ta có:
M =
x 1 1 2
- : + x - 1
x - 1 x - x x + 1
=
( ) ( ) ( ) ( )
x 1 x - 1 2
- : +
x - 1 x ( x - 1) x - 1 x + 1 x - 1 x +1
=
( ) ( ) ( ) ( ) ( ) ( )
x - 1 x + 1
x - 1 x + 1 x - 1
: = . x + 1
x x - 1 x - 1 x +1 x x - 1
=
x - 1
x
.
Vậy với x> 0; x≠1 thì
x - 1
x
M=
0,25
0,25
0,25
0,25
b) Với x> 0; x≠1, ta có:
M > 0
x - 1 > 0 (vì x > 0 nên
x
> 0)
x > 1. Kết hợp với x> 0;
x≠1
x > 1
Vậy với x> 1thì
0M>
0,25
0,25
Bài 3
(1,25
điểm):
a) Đường thẳng (d): y= 2x+ k đi qua B(-2: -1)
1 2( 2) 3k k
− = − + =
Vậy với k = 3 thì đường thẳng (d): y= 2x+ k đi qua B(-2:-1)
0,25
0,25
b) Với k =3 thì đường thảng (d) có dạng y = 2x+3
Hoaønh ñoä ñieåm chung cuûa (P) vaø (d) laø nghiệm của phöông
trình:
22
2 3 6 9 0
3
xx x x− = + + + =
Giải phương trình suy ra : x1 = x2 = -3=> y1 = y2 = -3
Vậy toaï ñoä ñieåm chung cuûa (P) vaø (d) laø : Q(-3 ;-3)
0,25
0,25
0,25
Bài 4
(3,0điểm)
x
1) Chứng minh được
ﾷ
ﾷ
ﾷ
0
90AEH ADH EAD= = =
Tứ giác ADHE là hình chữ nhật
0, 5
0,25
2) Chứng minh được AE.AB=AD.AC(=
2
AH
) 0,75
3) +) Từ AE.AB=AD.AC ( cmt)
AE AD
AC AB
=
- Chứng minh được
AED∆
ACB∆
(Vì có
ﾷ
à )
AE AD v BACchung
AC AB
=
ﾷ
ﾷ
ADE ABC=
Mà
ﾷ
ﾷ
0
180ADE EDC+ =
( 2 góc kề bù)
ﾷ
ﾷ
0
180ABC EDC + =
Tứ giác BCDE nội tiếp đường tròn
0,25
0,25
0,25
0,25
+) Cách 1: Kẻ tiếp tuyến Ax tại A của đường tròn tâm O
Chứng minh
ﾷ
ﾷ
xAB ACB=
và
ﾷ
ﾷ
AED ACB=
.
Suy ra
ﾷ
ﾷ
/ /AED xAB Ax DE=
.Mà
Ax AO AO ED
⊥ ⊥
0,25
0,25
Cách 2: - Tứ giác BCDE nội tiếp đường tròn( cmt)
ﾷ
ﾷ
AED ACB =
Mà
ﾷ
ﾷ
OAC OCA=
do
OAC
∆
cân tại O
ﾷ
ﾷ
ﾷ
( )OAC AED ACB = =
- Chứng minh được
EAD∆
AKD∆
( K là giao điểm của AO và ED)
ﾷ
ﾷ
ﾷ
ﾷ
0 0
à 90 90
EAD AKD
m EAD AKD AK ED AO ED taiK
=
= = ⊥ ⊥
0,25
0,25
Bài 5
(0,75
điểm):
Ta có :
3 2
2 2 2
x 2y 4y 3 0 (1)
x x y 2y 0 (2)
+ − + =
+ − =
Từ (1) ta có:
3 2
x 2(y 1) 1 1 x 1− − −−− =
(3) 0,25
0,25
Từ (2) ta có:
2 2
2
2y
x 1 x 1 1 x 1
y 1
− =
+
(4)
Từ (3) và (4), suy ra x = -1, thay vào hệ đã cho ta được y = 1.
Vậy P = 2.
0,25
* Lưu ý : - HS làm theo cách khác mà đúng thì vẫn cho điểm tối đa