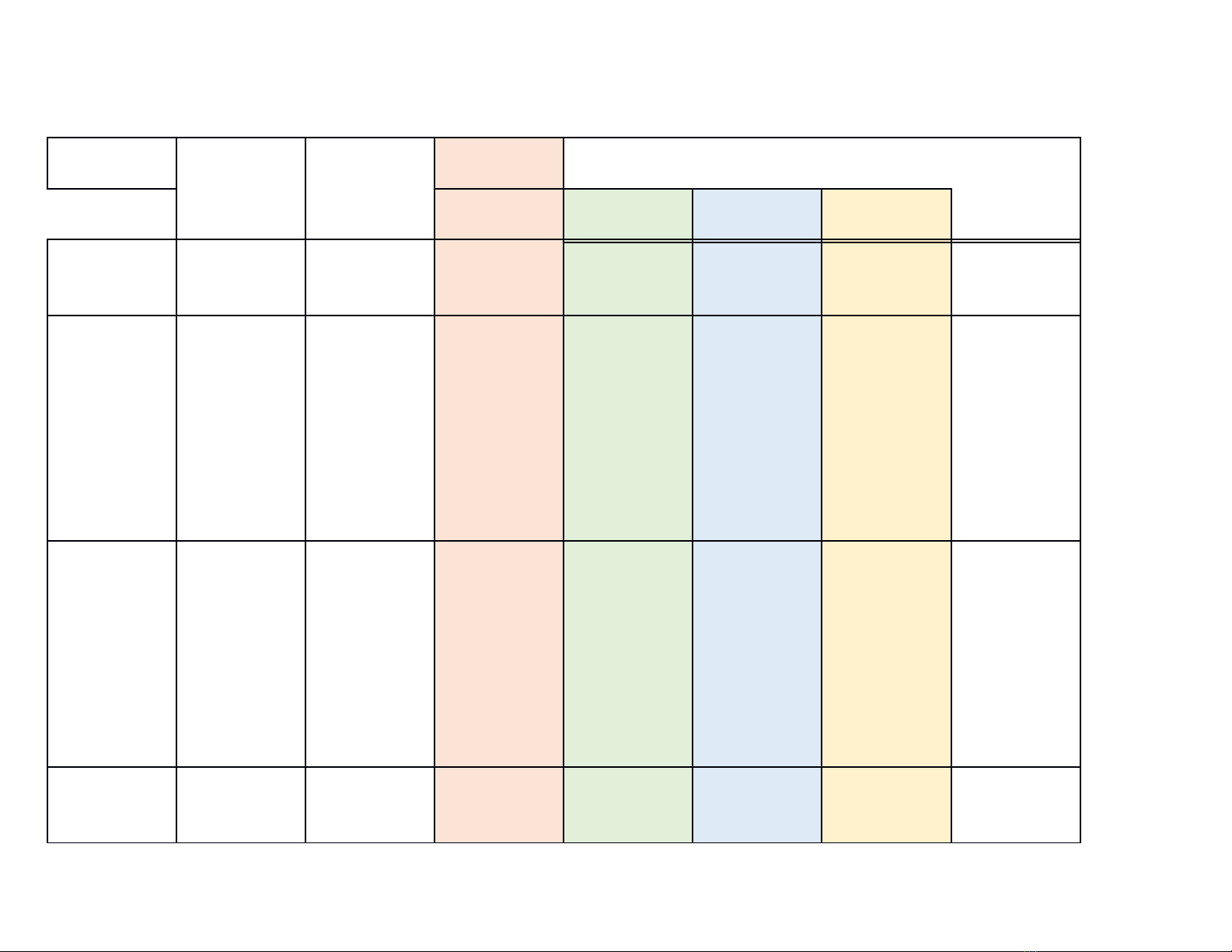
1A. KHUNG MA TRẬN ĐỀ KIỂM TRA GIỮA KỲ II MÔN TOÁN – LỚP 9
TT
Chủ đề
Nội
dung/Đơn
vị kiến thức
Mức độ
đánh giá Tổng % điểm
Nhận biết Thông hiểu Vận dụng Vận dụng
cao
1Căn bậc hai.
Các phép
tính trên căn
bậc hai.
2
(bài 1 ý 1;2)
(1,5đ)
1
(bài 1 ý 3)
(0,5đ)
3
2,0đ
2Toán thực tế
- Tỉ số
lượng giác.
- Giải bài
toán bằng
cách lập
phương
trình hoặc
hệ phương
trình.
2
(bài 2 ý1; 2)
(2đ)
2
2đ
3
Hệ phương
trình.
Phương
trình bậc hai
- Giải hệ
phương
trình.
- Vẽ Parabol
và đường
thẳng. Tìm
tọa độ giao
điểm của (d)
và (P)
1
(Bài 3 ý 1)
(1đ)
1
(bài 3 ý
2(a,b))
(1,5đ)
1
(bài 5)
(0,5đ)
3
3đ
4Đường tròn - Chứng
minh các
điểm cùng
1
(bài 4 ý 1)
1,25đ
1
(Bài 4 ý 2)
(1,25đ)
1
(bài 4 ý 3)
0,5đ
3
3,0đ
thuộc một
đường tròn
và các dạng
toán khác.
Tổng: Số
câu
Điểm
3
2,75đ
3
3,0đ
3
3,25đ
2
1đ
14
10đ
Tỉ lệ % 27,5% 30% 32,5% 10% 100%
Tỉ lệ chung 57,5% 42,5% 100%
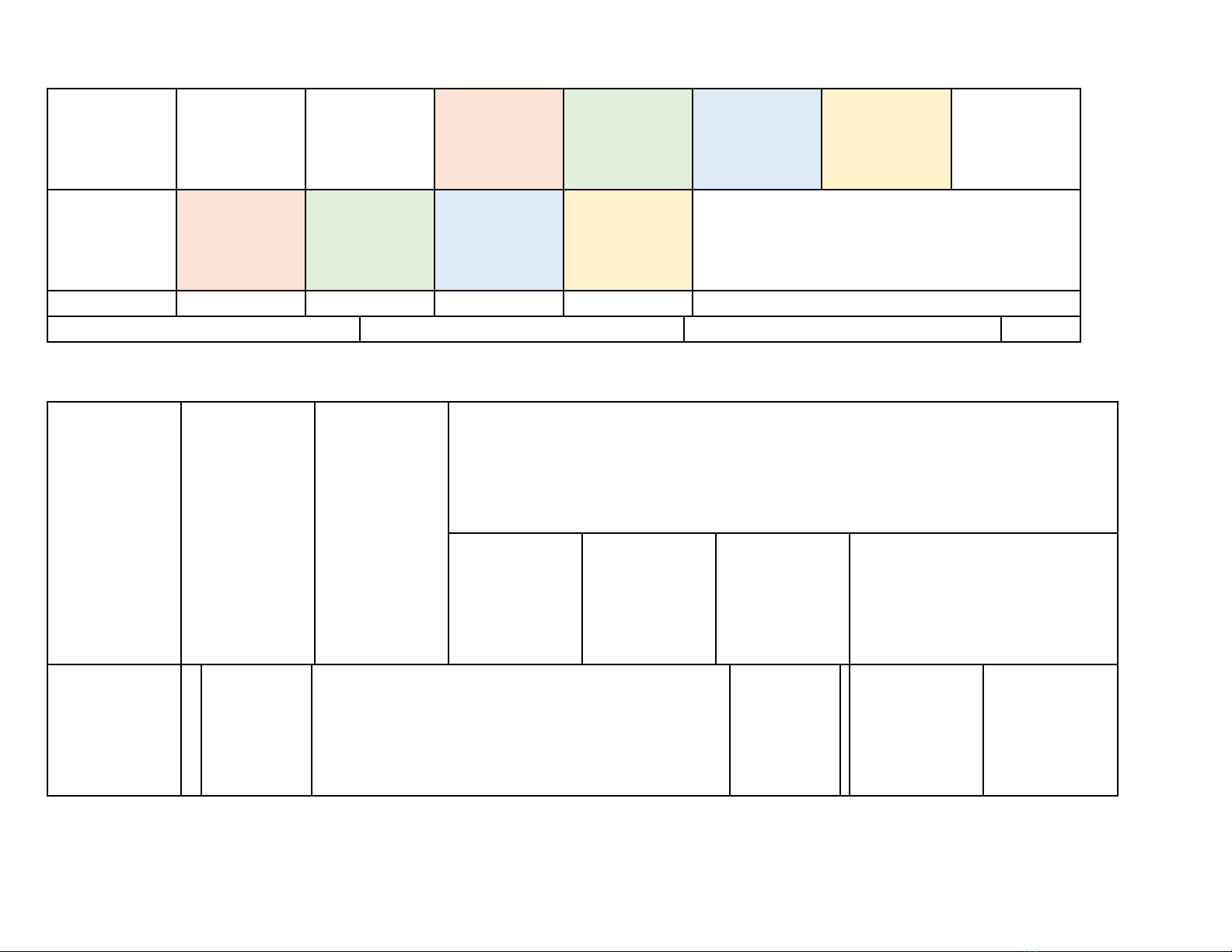
1B. BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ II TOÁN – LỚP 9
TT Chương/Ch
ủ đề
Mức độ
đánh giá
Số câu hỏi theo mức độ nhận thức
Nhận biết Thông hiểu Vận dụng Vận dụng cao
1 C
ă
n
b
Các phép
tính trên
căn bậc
hai.
Nhân biêt:
- Nhận biết được các công thức và các phép
tính thông thường của căn bậc hai
2
ậ
c
h
a
i
.
Vận dụng:
Vận dụng linh hoạt các kiến thức về căn bậc
hai để giải quyết các bài toán cần sự liên kết
và móc nối các kiến thức.
1
2 T
o
á
n
t
h
ự
c
t
ế
Tỉ số
lượng giác
và giải bài
toán bằng
cách lập
phương
trình, hệ
phương
trình
Thông hiểu:
– Học sinh nắm và hiểu được các công thức
của tỉ số lượng giác để làm bài tập tính toán
có gắn với thực tế.
-Hiểu và giải quyết được các bài toán chuyển
động trên thực tế.
3 H
ệ
p
h
- Giải hệ
phương
trình
- Phương
trình bậc
Thông hiểu:
Nắm vững kiến thức giải hệ cơ bản để áp dụng
vào giải hệ phương trình có lồng ghép các kiến
thức khác.
2
ư
ơ
n
g
t
r
ì
n
h
hai Vận dụng:
Vận dụng các kiến thức về hàm số y = ax + b và
y = ax2 để giải quyết bài tập dạng vẽ đồ thị hàm
số và tìm tọa độ giao điểm của hai đồ thị hàm số.
2
Vận dụng cao: Học sinh sử dụng một cách sáng
tạo các kiến thức về hệ phương trình kết hợp
thông minh với các kiến thức đã học để giải hệ
phương trình bậc cao.
1
4 Đ
ư
ờ
n
g
t
r
ò
n
Các điểm
cùng
thuộc một
đường
tròn và
các dạng
toán khác.
Nhân biêt:
Căn cứ vào các dữ kiện đầu bài đã cho chứng
minh được các điểm cùng thuộc một đường tròn.
1
Vận dụng:
Vận dụng linh hoạt các kiến thức đã học vào giải
các bài toán chứng minh hai đường thẳng vuông
góc, chứng minh hai tam giác đồng dạng.
Vận dụng cao:
Học sinh vận dụng một cách sáng tạo các kiến
thức đã học để giải quyết các bài tập khó, lạ, cần
vẽ thêm đường phụ…..
1