PHÒNG GD&ĐT TRỰC NINH
TRƯỜNG THCS TRỰC THUẬN
ĐỀ THI KIỂM TRA GIỮA HỌC KỲ II
MÔN : TOÁN – KHỐI 9
Năm học: 2022 – 2023
Thời gian: 90 phút (không kể thời gian giao đề)
I. TRẮC NGHIỆM (2 điểm) Hãy chọn đáp án đúng trong các câu sau:
Câu 1: Hàm số
( )
2
y 1 2 x
= −
là:
A. Nghịch biến trên R. B. Đồng biến trên R.
C. Nghịch biến khi x > 0, đồng biến khi x < 0 D. Nghịch biến khi x < 0, đồng biến khi x > 0
Câu 2. Trong các phương trình sau đây phương trình nào vô nghiệm:
A. x2 - 2x + 1 = 0 B. -30 x2 + 4x + 2011 C. x2 + 3x - 2010 D. 9x2 - 10x + 10
Câu 3. Cho
?
0
AOB 60
=
là góc của đường tròn (O) chắn cung AB. Số đo cung AB bằng:
A. 1200 B. 600 C. 300 D. Một đáp án khác
Câu 4: Cho hàm số
2
4
x
y=
và các điểm A(1; 0,25), B(2; 2) , C(4; 4). Các điểm thuộc đồ thị hàm số
là:
A. Chỉ A B. Chỉ B C. Chỉ A và B D. Chỉ A và C
Câu 5: Phương trình 3x2 – 7x – m + 1 = 0 có hai nghiệm phân biệt với m bằng:
A. m <
37
12
−
B. m >
37
12
−
C. m <
61
12
−
D. m >
61
12
−
Câu 6: Biết phương trình x2 – 2(m + 1)x – 2m – 4 = 0 có một nghiệm là – 2. Khi đó nghiệm còn lại
bằng:
A. 0B. 1C. 2D. 4
Câu 7: Tứ giác ABCD nội tiếp đường tròn, biết
ﾵ
ﾵ
C 3A=
. Số đo các góc A và C là:
A.
ﾵ
ﾵ
0 0
A 30 ; C 90
= =
B.
ﾵ
ﾵ
0 0
A 45 ; C 135
= =
C.
D.
ﾵ
ﾵ
0 0
A 60 ; C 120= =
Câu 8: Cho tam giác nhọn ABC ( AB < AC ) nội tiếp đường tròn (O). Các đường cao AD, BE, CF
và trực tâm H. Tứ giác nào sau đây nội tiếp được một đường tròn:
A. BFEC B. CEHD C. AEDB D. Cả 3 tứ giác trên.
II. TỰ LUẬN (8 điểm)
Bài 1 (1 đ): Cho hệ phương trình:
mx 2y 3 v�i m l� tham s�
2x my 11
+ =
− =
a. Giải hệ khi m = 2
b. Chứng tỏ rằng hệ luôn có nghiệm duy nhất với mọi giá trị của m.
Bài 2 (1,5 đ): Cho 2 hàm số: y =
2
1x
2
và y =
1x 1
2
+
a. Vẽ đồ thị hai hàm số trên cùng hệ trục tọa độ.
b. Tìm tọa độ giao điểm của hai đồ thị .
Bài 3( 1,5 điểm) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình.
Một hình chữ nhật có diện tích bằng 40 cm2. Nếu tăng chiều rộng thêm 3 cm và tăng chiều
dài tăng thêm 3 cm thì diện tích của hình chữ nhật tăng thêm 48 cm2.
Tính các kích thước ban đầu của hình chữ nhật.
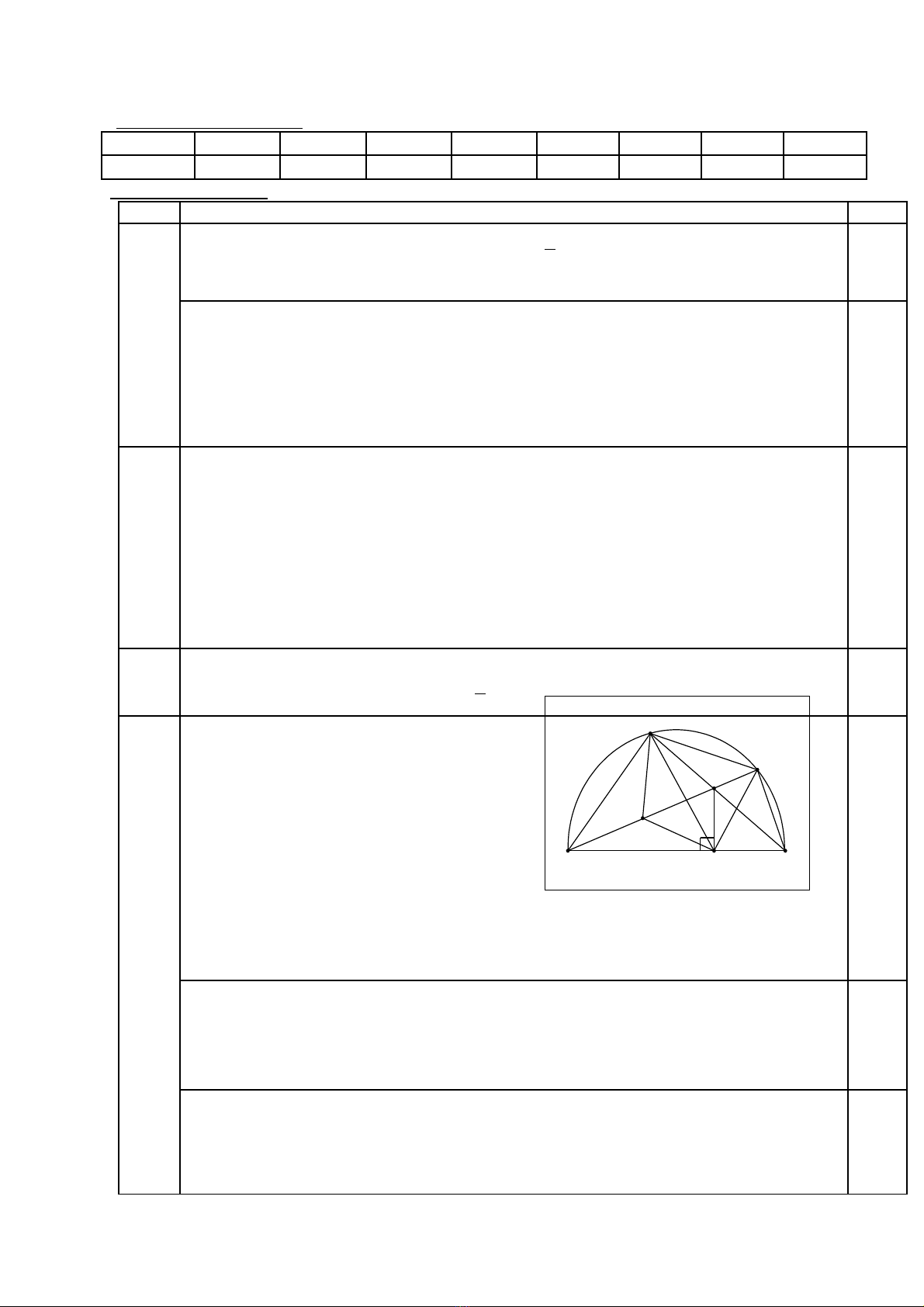
Bài 4 (3 đ): Cho tứ giác ABCD nội tiếp nửa đường tròn đường kính AD. Hai đường chéo AC và
BD cắt nhau tai E. Kẻ EF
⊥
AD. Gọi M là trung điểm của AE. Chứng minh rằng:
a. Tứ giác ABEF nội tiếp một đường tròn.
b. Tia BD là tia phân giác của góc CBF.
c. Tứ giác BMFC nội tiếp một đường tròn
Câu 5 (1,0 điểm) Giải phương trình:
( )
2
1 2 1 1 1 3 1x x x x x
+ + + = − + − + −
1
1
2
1
F
M
E
D
C
B
A
II. HƯỚNG DẪN CHẤM
I. Trắc nghiệm (2 điểm) Mỗi ý chọn đúng đáp án được 0,25 điểm.
Câu 1 2 3 4 5 6 7 8
Đáp án C D B D B A B D
II. Tự luận (8 điểm)
Bài Nội dung Điểm
Bài 1
(1,0 đ)
a. Với m=2 hệ trở thành:
7
2x 2y 3 x2
2x 2y 11 y 2
+ = =
− =
= −
0,5
b) Xét hệ:
mx 2y 3 v�i m l� tham s�
2x my 11
+ =
− =
Từ hai phương trình của hệ suy ra:
( )
+ = +
2
m 4 x 22 3m
(*)
Vì phương trình (*) luôn có nghiệm với mọi m nên hệ đã cho luôn có nghiệm với mọi
m.
0,25
0,25
Bài 2
(1,5 đ)
Gọi các kích thước của hình chữ nhật là x (cm) và y (cm) ( x; y > 0).
Theo bài ra ta có hệ phương trình:
( ) ( )
xy = 40 xy = 40
x + 3 y + 3 xy + 48 x + y = 13
=
.
Suy ra x, y là hai nghiệm của phương trình: t2 – 13t + 40 = 0 (1).
Giải phương trình (1) ta được hai nghiệm là 8 và 5.
Vậy các kích thước của hình chữ nhật là 8 cm và 5 cm.
0,25
0,5
0,25
0,5
Bài 3
(1,5đ
)
a. Vẽ đúng hai đồ thị
b. Tìm đúng tọa độ hai giao điểm (-1;
1
2
) và (2; 2)
1,0
0,5
Bài 4
(3 đ)
Hình vẽ:
a.Chỉ ra
?
0
ABD 90=
suy ra
?
0
ABE 90=
EF
⊥
AD suy ra
?
0
EFA 90=
Tứ giác ABEF có tổng hai góc đối bằng 900 nội tiếp được đường tròn
0,25
0,25
0,25
0,25
b. Tứ giác ABEF nội tiếp suy ra
?
?
1 1
B A=
( góc nội tiếp cùng chắn
?
EF
)
Mà
?
?
1 2
A B=
( nội tiếp cùng chắn cung CD)
Suy ra
?
?
1 2
B B=
suy ra BD là tia phân giác của góc CBF.
0,25
0,25
0,5
c. Chỉ ra tam giác AEF vuông tại F có trung tuyến FM
AMF ∆
cân tại M suy ra
?
?
1 1
M 2A=
Chỉ ra
?
?
1
CBF 2A=
suy ra
?
?
1
M CBF=
0,25
0,25
Suy ra B và M cùng nhìn đoạn CF dưới một góc bằng nhau và chúng cùng phía đối với
CF nên suy ra tứ giác BMFC nội tiếp một đường tròn 0,5
Bài 5
Câu 5 (1,0 điểm) Giải phương trình:
( )
2
1 2 1 1 1 3 1x x x x x
+ + + = − + − + −
Điều kiện: - 1 ≤ x ≤ 1
Với - 1 ≤ x ≤ 1 ta có
2
x 1 2(x 1) x 1 1 x 3 1 x+ + + = − + − + −
( )
2 2
x 1 1 x 2(x 1) 2 1 x 1 x 1 x 0
+ − − + + − − + − − − =
( ) ( ) ( )
x 1 1 x 2 x 1 x 1 1 x 1 x 1 x x 1 0+ − − + + + − − + − − − + =
0,25
( ) ( )
x 1 1 x 2 x 1 1 x 1 0+ − − + − − + =
x 1 1 x+ − −
= 0 hoặc
2 x 1 1 x 1+ − − +
= 0 0,25
Giải
x 1 1 x+ − −
= 0 tìm được x = 0 (tmđk)
0,25
Giải
2 x 1 1 x 1+ − − +
= 0 tìm được x =
24
25
−
(tmđk)
Vậy phương trình đã cho có nghiệm là x = 0; x =
24
25
−
0,25