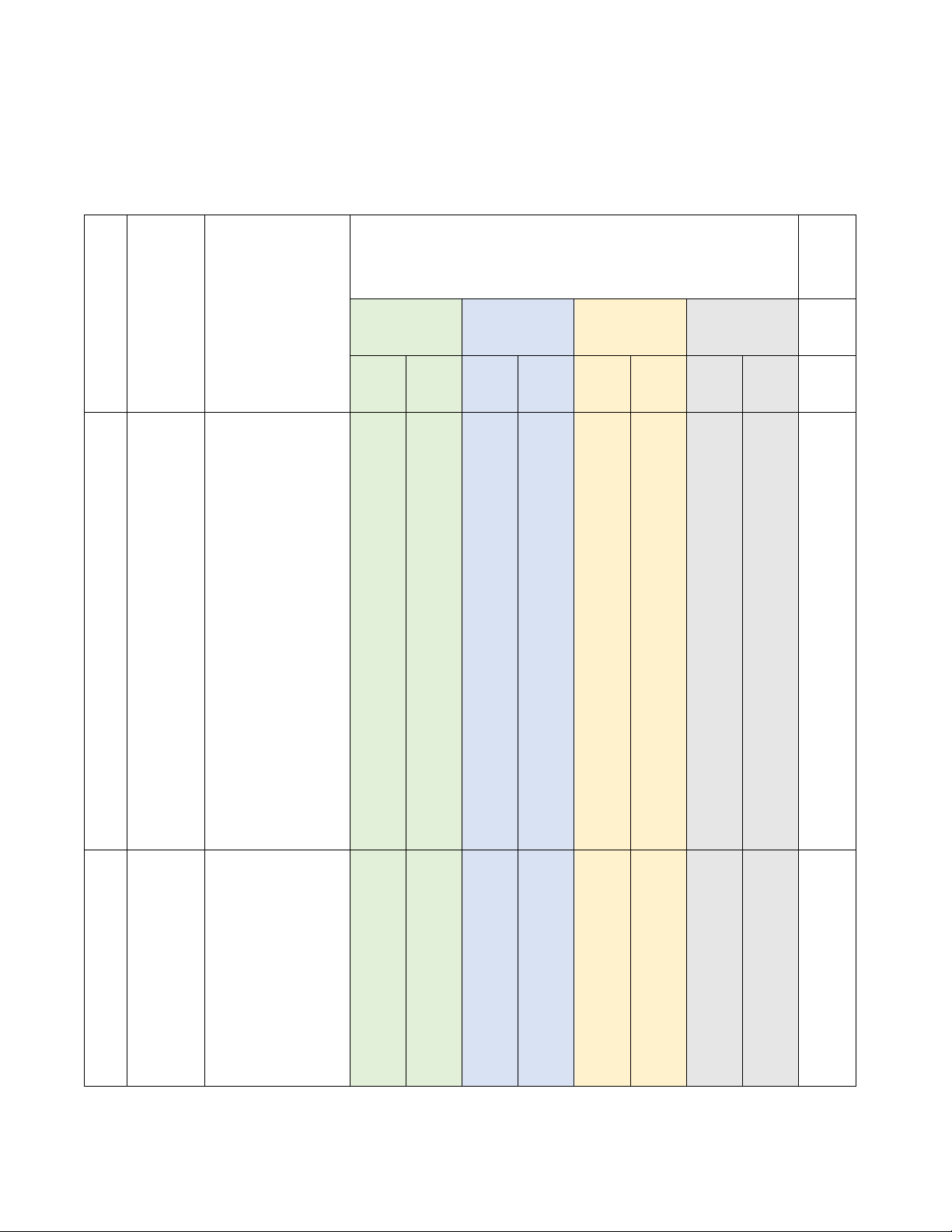
KHUNG MA TRẬN ĐỀ KIỂM TRA GIỮA KÌ II MÔN TOÁN – LỚP 8
NĂM HỌC 2023-2024
TT
Chủ đề
Nội dung/đơn vị
kiến thức
Mức độ đánh giá
Tổng
%
điểm
Nhận biết Thông hiểu Vận dụng
Vận dụng
cao
TNK
Q TL
TNK
Q TL
TNK
Q TL
TNK
Q TL
1
Chủ đề
1:
Hàm
số và
đồ thị
1/ Khái niệm
hàm số. Tọa độ
của một điểm và
đồ thị của hàm
số.
2/ Hàm số bậc
nhất
y = ax + b (a ≠
0) và đồ thị.
3/ Hệ số góc của
đường thẳng
y = ax + b. Hai
đường thẳng
song song, cắt
nhau.
4 câu
(1,0)
2 câu
(Bài
1a,b)
(1,0)
2 câu
(0,5)
3 câu
(Bài
1c,
2a,
3b)
(2,25
)
2 câu
(Bài
2b và
bài
3a)
(1,0)
57,5
%
2
Chủ đề
2:
Định lí
Thalès
1/ Định lí Thalès
trong tam giác.
2/ Đường trung
bình của tam
giác.
3/ Tính chất
đường phân giác
trong tam giác.
2 câu
(0,5) 2 câu
(0,5)
1 câu
(Bài
4)
(0,75
)
1 câu
(Bài
5a)
(1,0)
1 câu
(Bài
5b)
(1,0)
37,5
%
3
Chủ đề
3:
Hai
tam
giác
đồng
dạng
Bài 1. Hai tam
giác đồng dạng.
2 câu
(0,5) 5%
Tổng số câu
Tổng điểm
8
2,0
2
1,0
4
1,0
4
3,0 3
2,0 1
1,0
22
10,0
Tỉ lệ % 30% 40% 20% 10% 100
%
Tỉ lệ chung
70% 30%
100
%
UBND QUẬN BÌNH THẠNH ĐỀ KIỂM TRA GIỮA KỲ 2 NĂM HỌC 2023 - 2024
TRƯỜNG THCS ĐỐNG ĐA MÔN TOÁN LỚP 8
Thời gian: 90 phút (không kể thời gian phát đề)
I.TRẮC NGHIỆM (3,0 điểm)
Câu 1. Trong những điểm sau, điểm nào thuộc đồ thị hàm số
A.
( )
1;1
B.
( )
−
1; 1 C.
( )
2;0
D.
( )
−1; 2
Câu 2. Trong các trường hợp sau, trường hợp nào là hàm số bậc nhất
A.
=−+
1
y1
x
B.
= −
2
yx 1
C.
= − 2x
y2 3
D.
= +y 2x 3
Câu 3. Nếu hai đường thẳng d1 :
34yx=−+
và d2 :
( 2)y m xm=++
song song với nhau thì
m bằng :
A. – 2 B. – 5 C.3 D. – 3
Câu 4: Đường thẳng song song với đường thẳng d: y = –2x và cắt trục tung tại điểm có
tung độ bằng 3 là:
A. y = –2x – 3 B. y = 2x – 3 C. y = –2x + 3 D. y = 2x + 3
Câu 5: Cho hàm số
3
3
x
y−+
=
.Phát biểu nào sau đây là đúng về hàm số đã cho:
A. Là đường thẳng đi qua gốc tọa độ.
B. Cắt trục tung tại điểm có tung độ là 3.
C. Là đường thẳng đi qua điểm (0;1)
D. Không phải là một đường thẳng
Câu 6: Cho hai đường thẳng
25
3
yx=−+
và
25
3
yx= +
. Hai đường thẳng đã cho:
A. Cắt nhau tại điểm có hoành độ là 5.
B. Song song với nhau.
C. Cắt nhau tại điểm có tung độ là 5.
D. Trùng nhau.
Câu 7:Nếu AD là tia phân giác của tam giác ABC ( D
∈
BC) .Trong các khẳng định sau
khẳng định nào đúng?
A.
DB BC
DC AC
=
B.
DB AB
DC AD
=
C.
DB AB
DC BC
=
D.
DB AB
DC AC
=
Câu 8: Cho tam giác ABC đồng dạng với tam giác DEF theo tỉ số đồng dạng k =
2
3
thì
tam giác DEF đồng dạng với tam giác ABC theo tỉ số đồng dạng là:
A.
2
3
; B.
4
6
; C.
4
9
; D.
3
2
Câu 9: Cho tam giác ABC,Biết DE//BC.Trong các khẳng định sau khẳng định nào sai?
A.
AB AE
DB EC
=
B.
AD AE
AB AC
=
C.
AE DE
AC BC
=
D.
DB DE
AB BC
=
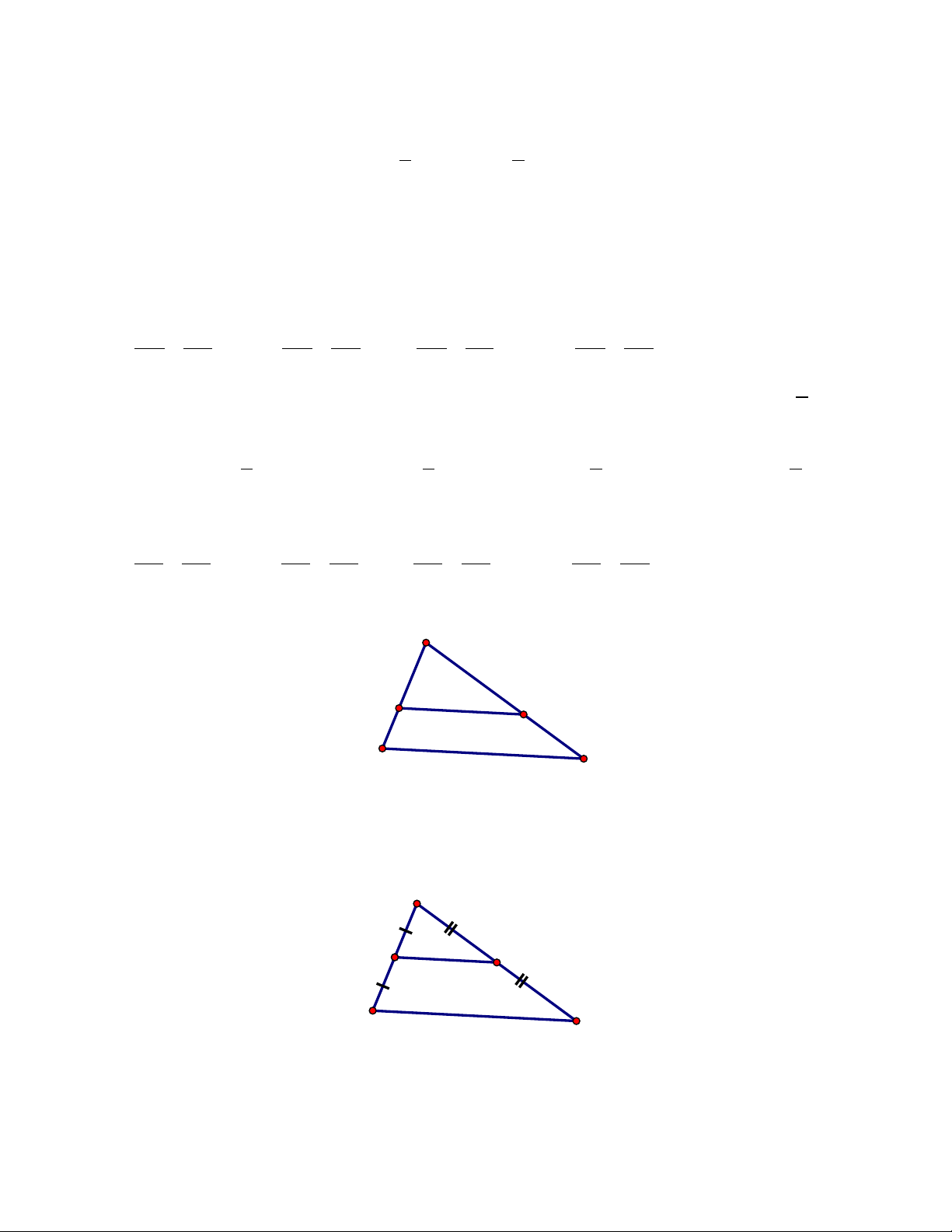
Câu 10: DE là đường trung bình tam giác ABC .Hãy tìm giá trị x.
A. 3 B. 12; C.6; D. 8
Câu 11: Cho hai đoạn thẳng AB =12 cm,CD = 10cm.Tỉ số của hai đoạn thẳng
AB và CD là
x
6
E
A
B
C
D
E
A
B
C
D
A.
5
6
AB
CD =
B.
6
5
AB
CD =
C.
4
3
AB
CD =
D.
3
4
AB
CD =
Câu 12:Biết MN // BC,AN = 4 cm, NC = 8 cm, MN = 5cm .Độ dài cạnh BC là
A. 10 cm B. 20 C.15 cm; D. 16 cm
II.TỰ LUẬN : ( 7 điểm)
Bài 1. a)Cho hàm số
3
() 2
5
y fx x= = −
. Tính
( ) ( )

−−


10
f 1 ,f 5 ,f 3
b) Cho hàm số
( 2) 5ym x=−−
(m
≠
2)
Với giá trị nào của m thì đồ thị hàm số đã
( 2) 5ym x=−−
song song với đường thẳng
34yx=−+
c) Với giá trị nào của m thì đồ thị hàm số
( 2) 5ym x=−−
đi qua điểm A(1; –2)
Bài 2. a)Vẽ đồ thị các hàm số sau đây trên cùng một mặt phẳng tọa độ:
y = –x + 3 và y =
2
3x
b) Cho hàm số
y ax b= +
xác định a,b biết đồ thị của đã cho song song với đường thẳng
y =
2
3x
và đi qua điểm A(–3;1)
Bài 3: Một hình chữ nhật có chiều rộng và chiều dài lần lượt là 10cm và 15cm. Gọi y
(cm) là chu vi của hình chữ nhật sau khi đã giảm mỗi kích thước là x (cm).
a/ Viết công thức biểu thị y theo x. Hỏi y có phải là hàm số bậc nhất của x không ?
b/ Tính chu vi y của hình chữ nhật sau khi giảm mỗi kích thước là 4cm.
N
A
B
C
M
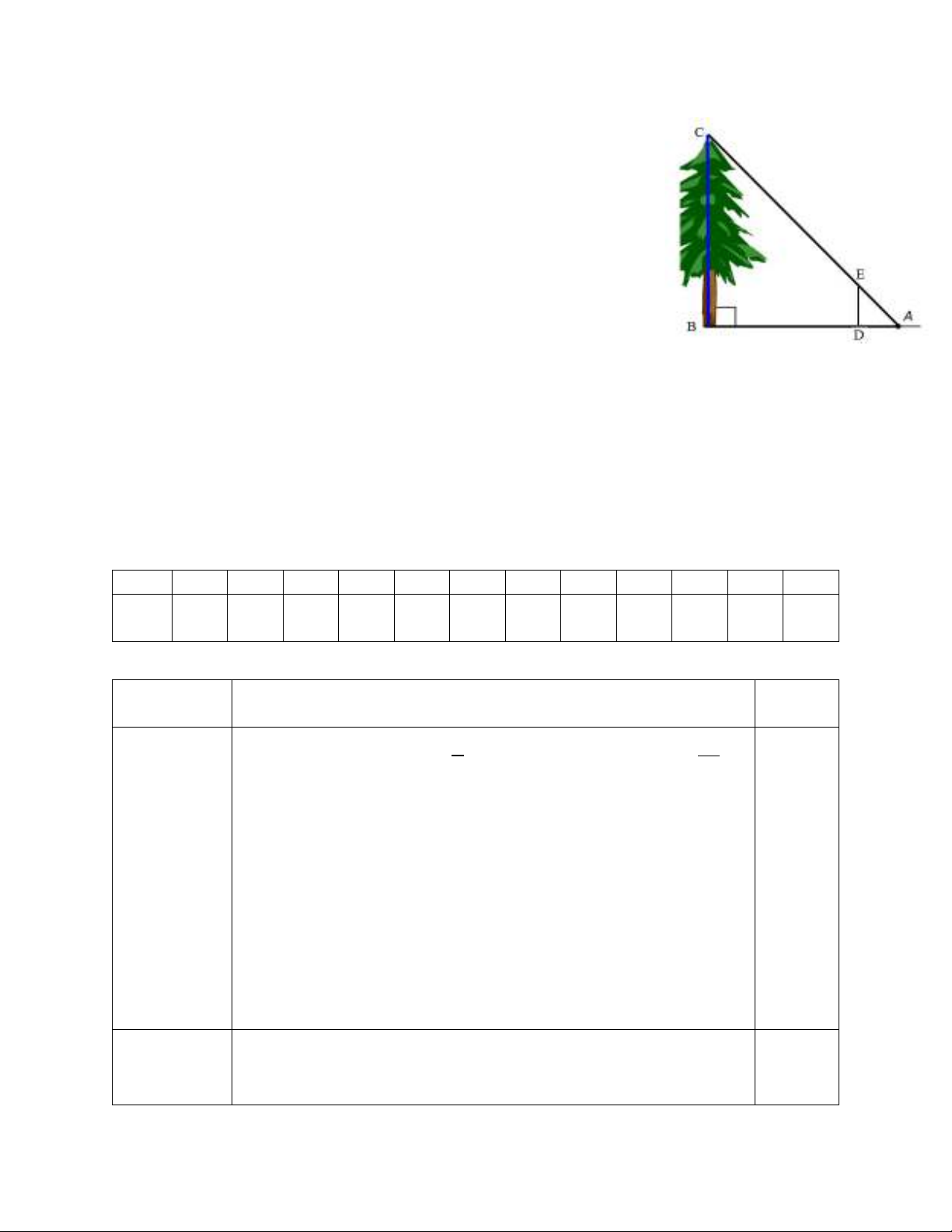
Bài 4: Để đo chiều cao của một cây mọc vuông góc với mặt đất
nằm ngang, một học sinh đã đặt giác kế vuông góc với mặt đất,
ngắm lên ngọn cây (C) rồi sau đó tìm điểm A trên mặt đất sao cho
các điểm C, E và A thẳng hàng (như hình vẽ). Bạn đó đã xác định
được các số đo: DE = 1,2m; DA = 1,4m; DB = 6m. Bằng kiến
thức đã học em hãy tính toán chiều cao của cây với đơn vị là mét
và làm tròn đến 2 chữ số thập phân.
Bài 5: Cho tam giác ABC vuông tại A, biết
AB = 9 cm
và
AC = 12 cm.
Tia phân giác của góc BAC cắt cạnh BC tại điểm D.
Qua D vẽ DE // AB (E thuộc AC).
a) Tính BC,DB,DC?
b) Tính DE ,diện tích tam giác ABE ?
ĐÁP ÁN
PHẦN I. TRẮC NGHIỆM (3,0 điểm) Mỗi ý trả lời đúng được 0,25 điểm.
Câu
1
2
3
4
5
6
7
8
9
10
11
12
Đáp
án
D
C
B
C
C
C
D
D
D
B
B
C
PHẦN II. TỰ LUẬN (8điểm).
Bài
Nội dung
Thang
điểm
1(1,5 điểm)
a)Cho hàm số
3
() 2
5
y fx x= = −
. Tính
( ) ( )

−−


10
f 1 ,f 5 ,f 3
b) Cho hàm số
( 2) 5ym x=−−
(m
≠
2)
Đồ thị hàm số đã
( 2) 5ym x=−−
song song với đường
thẳng
34yx=−+
Khi :m – 2 = -3 và -5
≠
4
=>m = - 1 (nhận)
c) Đồ thị hàm số
( 2) 5ym x=−−
đi qua điểm A(1; –2) nên ta
có : – 2 = ( m – 2 )(1) – 5
=> – 2 = m – 2 – 5
=> – 2 = m – 7
=> m = 5 (nhận)
0,5
0,25
0,25
0,25
0,25
2(2 điểm)
. a)Vẽ đồ thị các hàm số sau đây trên cùng một mặt phẳng tọa
độ: