S GD&ĐT THÁI NGUYÊNỞ
TR NG THPT PHÚƯỜ
BÌNH
Đ CHÍNH TH CỀ Ứ
Đ THI H C K II NĂM H C 2017 - 2018 Ề Ọ Ỳ Ọ
MÔN TOÁN. KH I 12 Ố
Th i gian làm bài 60 phút (không k th i gian giao đ)ờ ể ờ ề
H , tên thí sinh:.................................................................SBD:.......................ọMã đ thi: 134ề
Câu 1: Cho
3
1
3 1
ln
em
e
x xdx n
+
=
. Tính m.n?
A. m.n = 46 B. m.n = 12 C. m.n = 4 D. m.n = 64
Câu 2: : Trên m t ph ng t a đ, cho đi m ặ ẳ ọ ộ ể
M
(nh hình v ) là đi m bi u di n c a s ph c ư ẽ ể ể ễ ủ ố ứ
z
.
Tìm
z
?
A.
3 2z i
= +
.B.
3 2z i
= − −
.
C.
3 2z i
= − +
D.
3 2z i
= −
Câu 3: T p h p đi mậ ợ ể bi u di n s ph c ể ễ ố ứ
− =
z 2i 3
là đng tròn tâm ườ
I
. Tìm t t c các giá trấ ả ị
m đ kho ng cách t ể ả ừ
I
đn ế
d
:
3 4 - 0x y m
+ =
b ng ằ
1
5
.
A.
B.
C.
8; 8m m
= = −
D.
7; 9m m
= − =
Câu 4: Trong không gian v i h t a đ Oxyz, ớ ệ ọ ộ cho
( ; ; ), ( ; ; )
A A A B B B
A x y z B x y z
. Ch n kh ng đnhọ ẳ ị
đúng trong các kh ng đnh sau:ẳ ị
A.
2 2 2
( ) (y ) (z )
B A B A B A
AB x x y z= − + − + −
uuur
.B.
( ; y ;z )
A B A B A B
AB x x y z
= − − −
uuur
.
C.
( ; y ; z )
B A B A B A
AB x x y z
= − − −
uuur
. D.
( ; y ; z )
A B A B A B
AB x x y z
= + + +
uuur
.
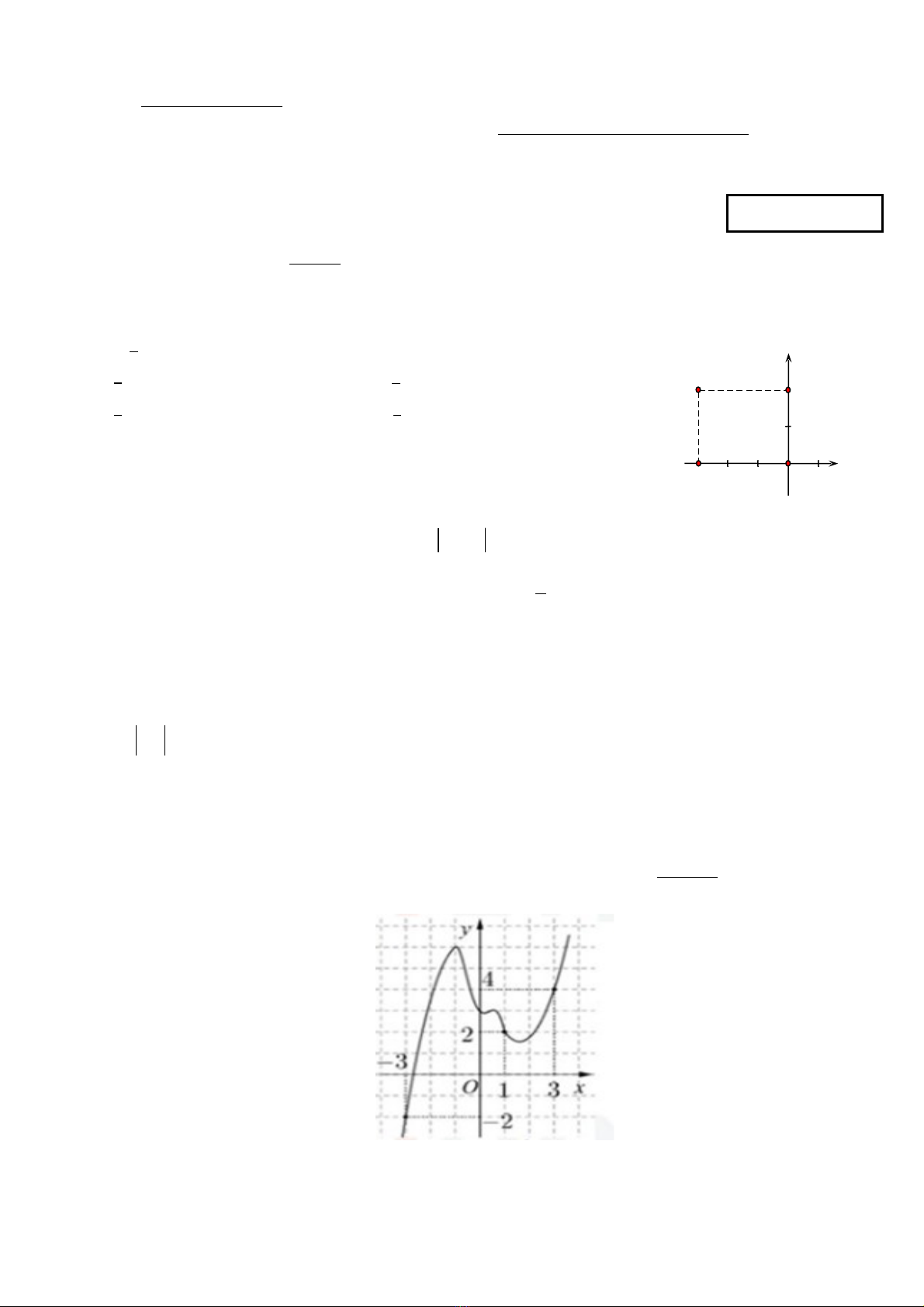
Câu 5: Cho hàm s ố
( )y f x
=
có đo hàm liên t c trên đo n ạ ụ ạ
[ ]
3;3−
. Hàm s ố
'( )y f x
=
có đ thồ ị
(nh hình vư ẽ) và
(1) 6f
=
. Tìm s nghi m c a ph ng trình ố ệ ủ ươ
( )
2
1
( ) 2
x
f x
+
=
trên đo n ạ
[ ]
3;3−
?
A. 3B. 2C. 1D. 0
Câu 6: Tìm 2 s th c x, y th a: ố ự ỏ
x(3 2i) y(1 4i) 1 24i
+ + − = +
A.
5; 2x y
= = −
B.
5; 2x y
= =
C.
2; 5x y
= = −
D.
2; 5x y
= = −
Trang 1/5 - Mã đ thi 134ề
Ox
y
3−
2
1
M
Câu 7: . Cho s ph c ố ứ
1
2 3z i
= − +
và
21 2z i= −
. Tìm ph n o c a s ph c ầ ả ủ ố ứ
2 1
z z
−
.
A.
5
B.
5
−
C.
3
D.
1
Câu 8: Trên t p s ph c ậ ố ứ
C
, hãy tìm các căn b c hai c a s -16.ậ ủ ố
A.
4
B.
16i
C.
4i
D.
4i
Câu 9: . Bi t ế
2
0
( ) 3f x dx
=
. Tính
4
0
( )
2
x
I f dx=
?
A. 36 B. 6C. 3D. 4
Câu 10: Trong không gian v i h t a đ Oxyz,ớ ệ ọ ộ cho đng th ng d: ườ ẳ
3
1 ,
2
x t
y t t
z t
= +
= − −
=
ﾡ
và m tặ
ph ng ẳ
( )
: 2 8 0P x y z
− − − =
. Tìm t a đ giao đi m ọ ộ ể
M
c a d và (P).ủ
A.
( )
3; 1;0M
−
B.
( )
4; 2;2M
−
C.
( )
2;2; 4M
− −
D.
( )
1; 4; 2M
−
Câu 11: Cho tích phân
4
2
0
1dI x x x
= +
và đt ặ
2
1t x
= +
. Kh ng đnh nào sau đây đúng?ẳ ị
A.
17
1
1d
2
I t t=
.B.
4
0
2 dI t t=
.C.
4
0
1d
2
I t t=
.D.
17
1
2 dI t t=
.
Câu 12: Cho hình ph ng ẳ
H
gi i h n b i đ th hàm s ớ ạ ở ồ ị ố
cosy x
=
, tr c hoành và hai đngụ ườ
th ng ẳ
0, 2x x
π
= =
. Tính th tích ể
V
c a kh i tròn xoay sinh b i ủ ố ở
H
quay quanh tr c hoành.ụ
A.
V
π
=
B.
2
4
V
π
π
= +
C.
2
2V
π
=
D.
2
V
π
=
Câu 13: Trong không gian v i h t a đ Oxyz,ớ ệ ọ ộ cho m t c uặ ầ
( ) ( ) ( ) ( )
2 2 2
: 2 1 3 16S x y z− + − + + =
. Tìm t a đ tâm I và tính bán kính R c a (S).ọ ộ ủ
A.
(2; 1;3), 4I R
− =
B.
(2;1; 3), 4I R
− =
C.
( 2; 1;3), 16I R
− − =
D.
(2; 1; 3), 16I R
− − =
Câu 14: Trong không gian v i h t a đ Oxyz, tìm t a đ c a ớ ệ ọ ộ ọ ộ ủ
a
r
bi t ế
2 3a i k j
= − +
r r r r
A.
( )
2; 3;1a
−
r
B.
( )
2;3; 1a
− −
r
C.
( )
2;1; 3a
−
r
D.
( )
3; 1;0a
−
r
Câu 15: Trong không gian v i h t a đ Oxyz, ớ ệ ọ ộ cho m t ph ng ặ ẳ
( )
: 2 2 4 0P x y z
− + + =
và đi mể
( )
2; 1;3A
−
.Tính kho ng cách d t đi m A đn mp(P) .ả ừ ể ế
A.
5
3
d=
B.
3d=
C.
5d
=
D.
1
5
d
=
Câu 16: Bi t ế
a,b
ﾡ
th a mãn ỏ
( )
3
b
2x 1dx a 2x 1 C
+ = + +
. Tính a - b?
A.
24
a b 23
−
− =
B.
7
a b 12
− = −
C.
12
a b 7
− = −
D.
23
a b 24
−
− =
Câu 17: G iọ
1 2
,z z
là hai nghi m ph c c a ph ng trình ệ ứ ủ ươ
2
2 0
10z z
=
− +
. Tính giá tr c a bi uị ủ ể
th c ứ
2 2
1 2
3P z z
= +
Trang 2/5 - Mã đ thi 134ề
A. 40 B. 41 C. 42 D. 43
Câu 18: Cho hàm s ố
( )
f x
liên t c trên ụ
[ ]
;a b
,
( )
;c a b
. Kh ng đnh nào d i đâyẳ ị ướ sai?
A.
( ) ( )
d d
b a
a b
f x x f x x
= −
� �
.B.
( ) ( ) ( ) ( )
d d d
b b b
a a a
f x g x x f x x g x x
+ = +
� �
� �
� � �
C.
( ) ( ) ( )
. ( ) d d . d
b b b
a a a
f x g x x f x x g x x
� �� �
=
� � � �� �
� � � �� �
� � �
D.
( ) ( ) ( )
d d d
c b b
a c a
f x x f x x f x x
+ =
� � �
.
Câu 19: Trong không gian v i h t a đ Oxyz, cho hình thang cân ớ ệ ọ ộ
ABCD
có hai đáy
AB
và
CD
th a mãn ỏ
2CD AB
=
và di n tích hình thang ệ
ABCD
b ng 27 , đnh ằ ỉ
( 1; 1;0)A
− −
,ph ngươ
trình đng th ng ch a c nh CD là ườ ẳ ứ ạ
2 1 3
2 2 1
x y z
− + −
= =
.Tìm t a đ đi m D bi t hoành đọ ộ ể ế ộ
đi m B l n h n hoành đ đi m A.ể ớ ơ ộ ể
A.
( 2; 5;1)D
− −
B.
(2;5;1)D
C.
(2; 5;1)D
−
D.
( 2;5;1)D
−
Câu 20: Cho ba s ph c ố ứ
1 2 3
, ,z z z
th a mãn ỏ
1 2 3
1z z z
= = =
và
1 2 3
1z z z
+ + =
. M nh đ nàoệ ề
sau đây sai?
A. Trong ba s ph c trên có nhi u nh t hai s b ng 1;ố ứ ề ấ ố ằ
B. Trong ba s ph c trên ph i có m t s b ng 1;ố ứ ả ộ ố ằ
C. Tích c a ba s ph c trên luôn b ng 1.ủ ố ứ ằ
D. Trong ba s ph c trên có hai s đi nhau;ố ứ ố ố
Câu 21: Cho s ph c ố ứ
2 3z i
= −
. Tìm s ph c liên h p ố ứ ợ
z
c a ủ
z
.
A.
2 3z i
= − −
B.
2 3z i
= − +
C.
2 3z i= +
D.
3 2z i= +
Câu 22: Trong không gian v i h t a đ Oxyz,ớ ệ ọ ộ cho hai m t ph ng (P):ặ ẳ
3 9 0;x y mz- + - =
(Q):
2 2 3 0x ny z+ + - =
. Tìm các giá tr c a ị ủ m và n đ hai m t ph ng song song .ể ặ ẳ
A.
2
3; 3
m n= =
B.
2
3; 3
m n= - =
C.
2
3; 3
m n= - = -
D.
2
3; 3
m n= = -
Câu 23: Tính tích phân
2
1
ln d
e
I x x x
=
.
A.
( )
3
12 1
3
I e= +
.B.
( )
3
12 1
9
I e= +
.C.
( )
3
12 1
9
I e= − +
.D.
( )
3
12 1
9
I e= −
.
Câu 24: Trong không gian v i h t a đ Oxyz, cho m t c u (S) có ph ng trình ớ ệ ọ ộ ặ ầ ươ
2 2 2
2 4 6 11 0x y z x y z+ + − + + − =
và mp(P)
2 2 7 0x y z
− + − + =
. M t ph ng (P) c t m t c uặ ẳ ắ ặ ầ
(S) theo giao tuy n là m t đng tròn .Tính di n tích ế ộ ườ ệ
S
c a đng tròn đó.ủ ườ
A.
16S
π
=
B.
8S
π
=
C.
2
16S
π
=
.D.
4S
π
=
Trang 3/5 - Mã đ thi 134ề
Câu 25: Trong không gian v i h t a đ Oxyz,ớ ệ ọ ộ cho hai đng th ng: ườ ẳ
1
1 2
: 2 3
3 4
= +
= +
= +
x t
d y t
z t
,và
2
3 4 '
: 5 6 '
6 8 '
x t
d y t
z t
= +
= +
= +
. Trong các kh ng đnh d i đây, kh ng đnh nào đúng?ẳ ị ướ ẳ ị
A.
1 2
/ /d d
B.
1 2
d d
C.
1 2
,d d
chéo nhau D.
1 2
⊥
d d
Câu 26: Tính di n tích ệ
S
c a hình ph ng gi i h n b i đ th c a hai hàm sủ ẳ ớ ạ ở ồ ị ủ ố
3 2
2 1y x x x
= − − +
và
2
1y x x
= + +
.
A.
70
6
S=
.B.
71
6
S
=
.C.
72
6
S
=
.D.
5S
=
.
Câu 27: Trong không gian v i h t a đ Oxyz, cho t giác ABCD bi tớ ệ ọ ộ ứ ế
(0;1; 1); (1;1; 2); (1; 1;0); (0;0;1)A B C D
− −
. Vi t ph ng trình ế ươ
( )mp
α
đi qua
,A B
và chia t di nứ ệ
thành hai kh i ố
ABCE
và
ABDE
sao cho
3
ABCE
ABDE
V
V
=
.
A.
15 4 5 1 0x y z
− − + =
B.
15 4 5 1 0x y z
+ − − =
C.
15 4 5 1 0x y z
− + − =
D.
15 4 5 1 0x y z
− − − =
Câu 28: M nh đ nào sau đây ệ ề đúng
A.
sin d cosx x x C
= − +
.B.
sin d sinx x x C= − +
C.
sin d sinx x x C= +
D.
sin d cosx x x C= +
.
Câu 29: Trong không gian v i h t a đ Oxyz, cho đi m A(1;2;3) và hai đng th ngớ ệ ọ ộ ể ườ ẳ
1 2
2 2 3 1 1 1
: ; :
2 1 1 1 2 1
x y z x y z
d d
− + − − − +
= = = =
− −
. Vi t ph ng trình đng th ng d đi qua A,ế ươ ườ ẳ
vuông góc v i ớ
1
d
và c t ắ
2
d
.
A.
1 2 3
1 3 5
x y z
− + −
= =
−
B.
1 2 3
1 3 5
x y z
+ − −
= =
−
C.
1 2 3
1 3 5
x y z
+ − −
= = −
D.
1 2 3
1 3 5
x y z
− − −
= =
− −
Câu 30: Trong không gian v i h t a đ Oxyz, cho đng th ng d: ớ ệ ọ ộ ườ ẳ
1 2 3
1 2 3
x y z
− + −
= =
− −
. Vectơ
nào d i đây không ph i là m t vect ch ph ng c a đng th ng d?ướ ả ộ ơ ỉ ươ ủ ườ ẳ
A.
( )
1
1; 2;3 .u
= −
ur
B.
( )
2
1;2; 3u
= − −
uur
.C.
( )
4
2; 4;6u
= −
uur
.D.
( )
3
1;2;3u
=
uur
.
Câu 31: Tính
2 1
d
x
e x
+
.
A.
2 1 2
d
x x
e x e C
+
= +
.B.
2 1 2 1
1
d2
x x
e x e C
+ +
= +
C.
2 1 2 1
d
x x
e x e C
+ +
= +
.D.
2 1 2 1
d 2
x x
e x e C
+ +
= +
.
Trang 4/5 - Mã đ thi 134ề
Câu 32: Trong không gian v i h t a đ Oxyz, cho đi m ớ ệ ọ ộ ể
(3; 2; 2) ; B(1;-2;4) A
−
và
( ) : 6 0mp x y z
α
+ + − =
. Vi t ph ng trình m t ph ng ch a ế ươ ặ ẳ ứ
AB
và vuông góc v i ớ
( )mp
α
.
A.
5 4 9 0x y z
− − − =
B.
5 4 9 0x y z
− + − =
C.
5 4 9 0x y z
− − + =
D.
5 4 9 0x y z
+ − − =
----------- H T ----------Ế
Trang 5/5 - Mã đ thi 134ề