Trang 1/5- Mã đề thi 474
SỞ GD-ĐT BẮC NINH
TRƯỜNG THPT QUẾ VÕ 1
---------------
ĐỀ THI HỌC KỲ 2 - NĂM HỌC 2017-2018
MÔN: TOÁN 12
(Thời gian làm bài: 90 phút, không kể thời gian phát đề)
ĐỀ CHÍNH THỨC
Đề gồm có 5 trang, 50 câu
Mã đề: 474
Họ tên thí sinh:............................................................SBD:...............................................................
Câu 1: Giải bất phương trình
2
2 2
3 3
log 2 1 log 3
x x
A.
1
2
1
x
x
B.
x
C.
1
0
2
1
x
x
D. 1
1
2
x
Câu 2: Tìm m để đồ thị hàm số
2
1
2 1 3
x
yx m x m
có đúng một đường tiệm cận đứng
A.
2; 1;2
m B.
1;2
m
C.
1;2
m D.
; 1 2;m

Câu 3: Có bao nhiêu giá trị nguyên của m để hàm số
3
2 3
22 8
3
m x
y m x x m
nghịch
biến trên R
A. 9 B. vô số C. 6 D. 8
Câu 4: Trong các mệnh đề sau, có bao nhiêu mệnh đề nào đúng?
( I) Hàm số
y x
có tập xác định là
0;

(II) Hàm số
x
y a
( với
0 1
a
) đồng biến trên
;
 
(III) Đồ thị hàm số
log
a
y x
( với
0 1
a
) nhận trục tung làm tiệm cận đứng.
(IV)
log log log ; 0
ab a b ab
(V)
1000
2
có 301 chữ số trong hệ thập phân
(VI)
2
2 2
log 1 1 log ; \ 0
x x x R
A. 5 B. 2 C. 4 D. 3
Câu 5: Cho hàm số
( )
f x
liên tục trên đoạn
;
a b
. Chọn mệnh đề sai trong các mệnh đề sau.
A.
( ) ( )
b b
a a
f x dx f u du
B.
( ). ( ) ( ) . ( )
b b b
a a a
f x g x dx f x dx g x dx
C.
( ) ( )
b a
a b
f x dx f x dx
D.
( ) ( ) ( ) ( )
b b b
a a a
f x g x dx f x dx g x dx
Câu 6: Gọi
1 2
;
z z
là nghiệm của phương trình 2
2 10 0
z z
. Gọi A; B lần lượt là điểm biểu diễn
số phức
1 2
;
z z
trên mặt phẳng phức. Tính độ dài đoạn thẳng AB
A.
10
B.
2 10
C. 6 D. 2
Câu 7: Gọi
1 2
;
x x
là nghiệm của phương trình
6.4 13.6 6.9 0
x x x
. Tính
2 2
1 2
x x
A.
97
36
B. 2 C.
13
6
D. 0
Trang 2/5- Mã đề thi 474
Câu 8: Trong không gian với hệ tọa độ oxyz, cho hai mặt phẳng phân biệt
:3 2 2 5 0
x y z
và
: 4 5 10 0
x y z
, gọi đường thẳng
là giao tuyến của mặt phẳng
và
. Một véc
tơ chỉ phương của đường thẳng
là
A.
8; 11; 23
u
B.
4;5; 1
u
C.
8;11; 23
u
D.
3; 2;2
u
Câu 9: Biết
( )
F x
là nguyên hàm của
2
( ) 1
f x x
và
(2) 10
F
. Tìm
( 1)
F
A.
1
B.
0
C.
1
D.
2
Câu 10: Cho một khối đa diện đều. Khẳng định nào sau đây là SAI ?
A. Số cạnh của khối tứ diện đều bằng 6 B. Số đỉnh của khối lập phương bằng 8
C. Khối bát diện diện là loại
4;3
D. Số cạnh của khối bát diện đều bằng 12
Câu 11: Cho hàm số
32
2
3
3 3
x
y x
(C ). Tiếp tuyến của ( C) tại điểm
1;
M m
tạo với
hai trục tọa độ một tam giác . Tính diện tích tam giác đó.
A.
9
10
(đvdt) B.
9
5
(đvdt) C.
25
14
(đvdt) D. 5 (đvdt)
Câu 12: . Cho
2
1
2 .ln ln 2 , ;
I x xdx a b a Z b R
. Tính
.
a b
A.
19
2
B.
5
2
C.
5
2
D.
19
2
Câu 13: Thể tích của khối cầu ngoại tiếp hình lập phương
. ' ' ' '
ABCD A B C D
cạnh
2
bằng
A.
6
B.
3
C.
12
D.
6
Câu 14: Cho số phức
4 3
z i
. Tìm phần thực, phần ảo của số phức
1
z
A. Phần thực bằng
1
4
, phần ảo bằng
1
3
B. . Phần thực bằng
4
5
, phần ảo bằng
3
5
C. . Phần thực bằng
4
25
, phần ảo bằng
3
25
D. . Phần thực bằng
4
25
, phần ảo bằng
3
25
Câu 15: Cho lăng trụ tam giác đều .
ABC A B C
có
;AA ' 2
AB a a
. Tính góc giữa đường thẳng
A C
và mặt phẳng
AA B B
.
A.
0
45
B.
0
30
C.
0
90
D.
0
60
Câu 16: Tìm nguyên hàm của hàm số
cos 2
y x
A. 1sin 2
2
x C
B. 1sin 2
2
x C
C. 2sin 2
x C
D. 2sin 2
x C
Câu 17: Trong không gian với hệ tọa độ oxyz, cho điểm
1;4;2
M và mặt phẳng
: 2 2 5 0
x y z
. Tọa độ hình chiếu vuông góc của điểm M lên mặt phẳng
là
A.
1; 2;0
H B.
1;0; 2
H
C.
1;2; 5
H
D.
1;0; 3
H
Câu 18: Đồ thị hàm số nào sau đây luôn nằm dưới trục hoành:
A. 3 2
2 1
y x x x
B. 4 2
2 3
y x x
C. 4 2
4 1
y x x
D. 4 2
3 1
y x x
Câu 19: Cho hình chóp tam giác đều có tất cả các cạnh bằng
a
. Tính diện tích toàn phần của
hình chóp đó theo
a
A. 2
3
a B.
2
a
C.
2
3
4
a D.
2
3
2
a
Câu 20: Hàm số nào sau đây luôn đồng biến trên tập xác định của nó?
Trang 3/5- Mã đề thi 474
A.
32
2
3
x
y x x
B.
2
2 1
x
y
x
C. 3
2 5
y x x
D. 5 3
3 4
y x x
Câu 21: Cho số phức
;
z a bi a b R
. Mệnh đề nào sau đây là đúng?
A.
2
2
z z
B. Điểm
;
M a b
là điểm biểu diễn số phức
C. Mô đun của số phức z là một số thực dương
D.
z iz
Câu 22: Cho
( )
f x
liên tục trên
4;

và
5
0
4 8
f x dx
. Tính
3
2
. ( )
x f x dx
A.
4
B.
8
C.
4
D.
16
Câu 23: Tính tổng các nghiệm của phương trình: 2 2 2
3
(log 2 2).log 2 (log 2 1)
2
x x x
.
A.
4
. B.
8 2
2
. C.
8 2
2
. D.
2
2
.
Câu 24: Tìm nghiệm
0;
2
x
của phương trình 1
2 3 4
sin lim
1
t
t
x
t
A.
1
2
B.
3
C. vô nghiệm D.
6
Câu 25: Trong một nhóm có 9 học sinh trong đó có 4 bạn nữ, 5 bạn nam . Chon ngẫu nhiên 3
bạn trong nhóm đó. Tính xác suất để trong 3 bạn được chọn có ít nhất hai bạn nam.
A.
17
42
B.
5
14
C.
25
42
D.
10
21
Câu 26: Trong không gian với hệ tọa độ oxyz cho
2;3; 1 ; 2;1;3
A B, gọi I là trung điểm của
AB. Mệnh đề nào sau đây là đúng?
A.
OI i j k
B.
2 4
OI j k

C. 2 2
OI i j k
D.
2 4
OI i k
Câu 27: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
x
x
y
e
trên đoạn
1;1
A.
1,1
1,1
1
max ;min 0
y y
e
B.
1,1
1,1
max ;min 1
y e y
C.
1,1
1,1
1
max ;miny e y
e
D.
1,1
1,1
max ;min 0
y e y
Câu 28: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của
S lên mặt phẳng (ABCD) là điểm H thuộc cạnh AB sao cho
2
HB HA
, SC tạo với mặt phẳng
đáy (ABCD) một góc
0
60
. Tính khoảng cách từ trung điểm K của HC đến mặt phẳng (SCD).
A.
13
2
a B.
13
4
a C.
13
a D.
13
8
a
Câu 29: Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD) , đáy ABCD là hình
chữ nhật,
2 ;
AB a AD a
, SC tạo với đáy một góc
0
60
. Tính thể tích của khối chóp S.ABD theo
a
.
A.
3
2 15
3
a B.
3
15
3
a C. 3
2 15
a D. 3
15
a
Trang 4/5- Mã đề thi 474
Câu 30: Cho tam giác
ABC
vuông cân tại A có
AB a
. Tính diện tích toàn phần của hình nón
sinh ra khi quay tam giác ABC quanh cạnh AB
A. 2
2 2
a
B. 2
2
a
C.
2
2
a
D.
2
1 2
a
Câu 31: Trong mặt phẳng tọa độ
,
Oxy
Tìm điểm
'
M
là ảnh của điểm
6; 2
M
qua phép quay
tâm
2;1
I góc
0
90
A.
' 3;5
M B.
' 1; 3
M
C.
' 5; 5
M D.
' 2; 6
M
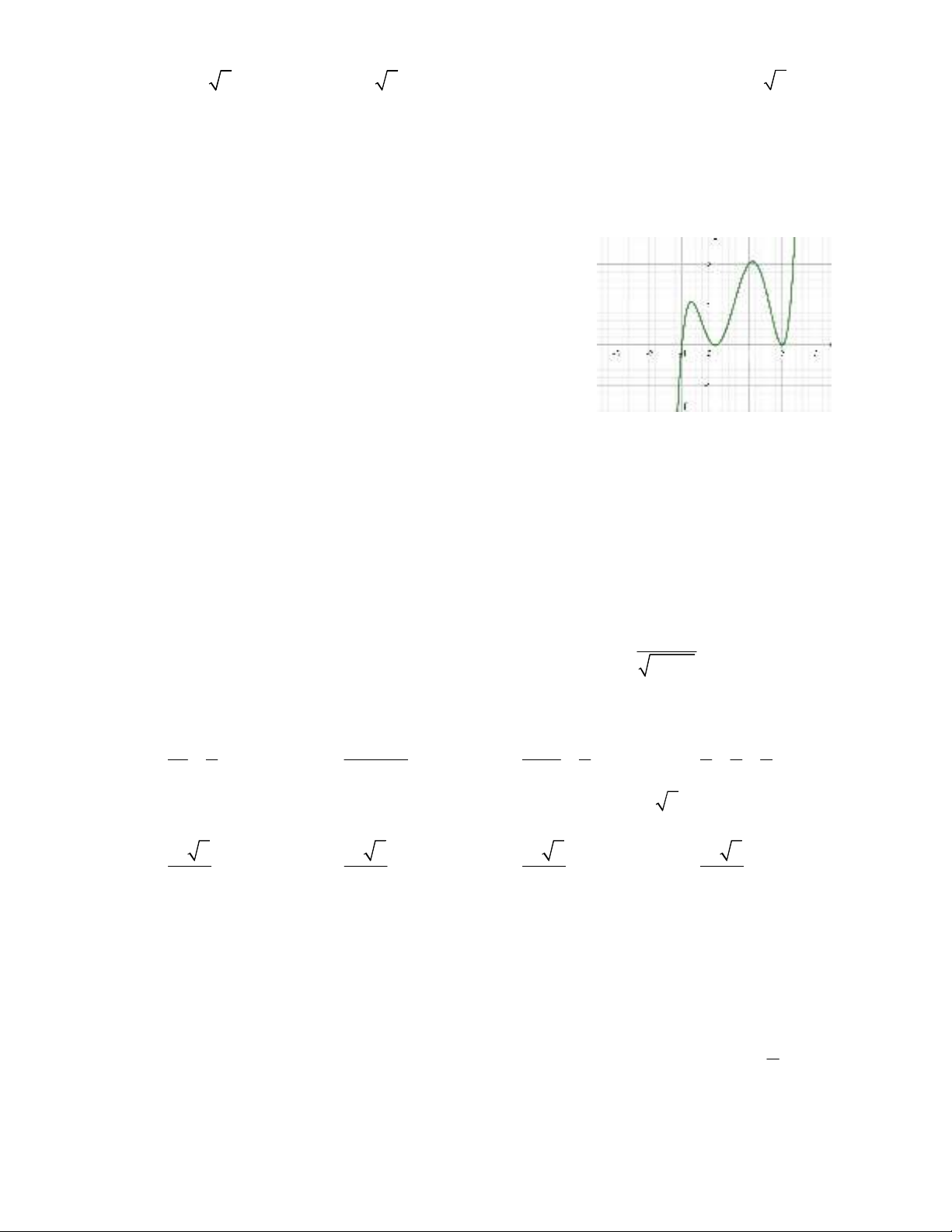
Câu 32:
Hàm số
f x
có đạo hàm
'
f x
trên K , hàm số
'
f x
có đồ thị như hình vẽ. Tìm số điểm cực trị
của đồ thị hàm số
f x
.
A. 2 B. 0 C. 1 D. 3
Câu 33: Tập xác định của hàm số
2
y x
là
A.
\ 2
R B.
2;
C.
2;

D.
0;

Câu 34: Trong không gian với hệ tọa độ oxyz , đường thẳng d đi qua điểm
1; 2;4
Mvà có một
véc tơ chỉ phương
3; 1;2
u
có phương trình là
A.
1 3
2
4 2
x t
y t
z t
B.
1 3
2
4 2
x t
y t
z t
C.
1 3
2
4 2
x t
y t
z t
D.
3
1 2
2 4
x t
y t
z t
Câu 35: Phương trình đường tiệm cận ngang của đồ thị hàm số 2
2 1
2
x
yx
A.
2; 2
x x
B.
2
y
C.
2
y
D.
2; 2
y y
Câu 36: Cho 2 5 3
log 3 ;log 4 ;log 7
a b c
. Tính 9
log 175
theo a,b,c?
A.
2 c
ab 2
B.
a b c
2
C.
2 c
a b 2
D.
222
abc
Câu 37: Cho lăng trụ đều ABC.A'B'C' , cạnh đáy bằng
a
,
' 2
AA a
. Tính thể tích của khối
ABC.A'B'C' theo
a
.
A.
3
6
4
a B.
3
6
12
a C.
3
6
24
a D.
3
6
2
a
Câu 38: Cho hàm số
( )
f x
liên tục trên R , biết
2
0
2 . '( ) 5; (0) 1
x f x dx f
. Tính
2
0
( )
I f x dx
A.
3
B.
7
C.
7
D.
Câu 39: Gọi
, ,
l h R
lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón (N).
Tìm khẳng định đúng
A. 2
xq
S Rl
B.
2
V R h
C.
tp
S R R h
D. xq
S Rl
Câu 40: Cho hai số phức
1 2
1 2 ; 4 ;
z i z x y i x y R
. Tìm cặp
;
x y
để
2 1
2
z z
A.
; 2;0
x y B.
; 2;6
x y C.
; 0;2
x y D.
; 2;8
x y
Trang 5/5- Mã đề thi 474
Câu 41: Đạo hàm của hàm số
1
2
x
y
là
A.
1
1
2
x
x
B.
1
2 ln 2
x C. 1
ln 2
2
x
D. 1
ln 2
2
x
Câu 42: Trong không gian với hệ tọa độ oxyz, mặt cầu có tâm
2;1; 1
I
và tiếp xúc với mặt
phẳng
: 2 2 4 0
x y z
có phương trình
A.
2 2 2
2 1 1 3
x y z
B.
2 2 2
2 1 1 3
x y z
C.
2 2 2
2 1 1 9
x y z
D.
2 2 2
2 1 1 9
x y z
Câu 43: Tìm giá trị thực của tham số
m
để hàm số 3 2 2
1
( 4) 3
3
y x mx m x
đạt cực tiểu tại
3
x
.
A.
5; 1
m m
B.
m
C.
1
m
D.
m
Câu 44: Tính
2
2 3
1
1
lim
1
x
x
x x x
A.

B.

C.
2
D.
2
Câu 45: Tìm cực đại của hàm số
42
2 6
4
x
y x
A. 2 B. 0 C. 6 D.
0;6
Câu 46: Một hình trụ
T
có bán kính đáy 2 cm và có thiết diện qua trục là hình vuông . Tính
diện tích xung quanh của khối trụ
T
.
A.
2
8
cm
. B.
2
4
cm
C.
2
16
cm
. D.
2
16
3
cm
Câu 47: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
4
y x
và trục hoành
A.
512
15
B.
25
3
C.
23
3
D.
32
3
Câu 48: Tìm giá trị nhỏ nhất và lớn nhất của hàm số
2x 1
y
x 1
trên
2;0
A. Không tồn tại giá trị lớn nhất ;
2;0
min 1
y
B. Không tồn tại giá trị nhỏ nhất;
2;0
max 5
y
C. Không tồn tại giá trị lớn nhất và giá trị nhỏ nhất của hàm số
D.
2;0 2;0
min 1;max 5
y y
Câu 49: Tìm số phức z thỏa mãn
2 1 4 2
i i z i
.
A.
1 3
z i
B.
1 3
z i
C.
1 3
z i
D.
1 3
z i
Câu 50: Tìm m để hàm số
1 2
3
( ) 3
3
xkhi x
f x x
m khi x
liên tục tại
3
x
.
A.
1
4
m
B.
4
m
C.
1
4
m
D.
m
-----------------------------------------------
----------- HẾT ----------