I. Đ :Ề
Bài 1: (2.0đ). Cho hàm s ố
2
2 2y x x= − + +
có đ th (P).ồ ị
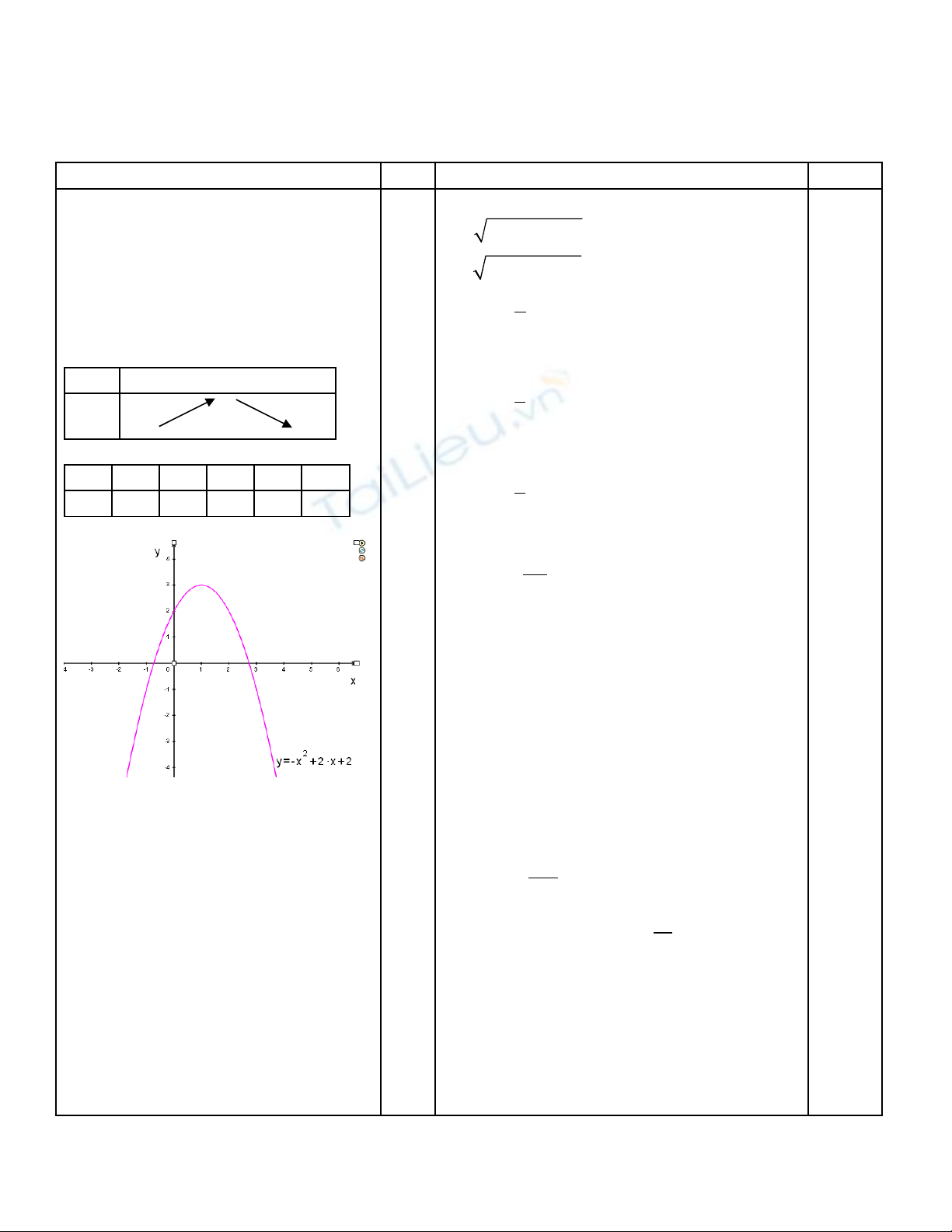
a/ Kh o sát s bi n thiên và v đ th (P) c a hàm s .ả ự ế ẽ ồ ị ủ ố
b/ Tìm t a đ giao đi m c a đ th (P) và đ ng th ng d: ọ ộ ể ủ ồ ị ườ ẳ
5 4y x= +
.
Bài 2: (1.5đ) Tìm đi u ki n c a ph ng trình:ề ệ ủ ươ
2
) 3
24
x
a x
x= −
−
.
4
) 2
1
x
b x
x
+= −
−
.
Bài 3: (2.0đ).Gi i các ph ng trình và h ph ng trình sau:ả ươ ệ ươ
2
/ 7 10 1 3a x x x
− + + =
.
3 1 6 1
/3 2 4
x x
bx x
+ +
=
− +
2 3 13
/7 4 2
x y
cx y
− =
+ =
(không b m máy tính). .ấ
Bài 4: (0.75đ). Gi i và bi n lu n ph ng trình sau: ả ệ ậ ươ
(2 1) 5 0.m x x− + + =
Bài 5: (0.75đ). Cho ph ng trình: ươ
2
(2 1) 5 0mx m x m− + + − =
Tìm m đ ph ng trình có hai nghi m phân bi t.ể ươ ệ ệ
Bài 6: (1.25đ). Cho tam giác ABC vuông cân t i B có BC=a, đ ng cao BH.ạ ườ
a/ Xác đ nh ị
b/ Tính
.AH BC
uuur uuur
.
Bài 7: (1.75đ). Trong m t ph ng Oxy cho ba đi m A(3;4), B(2;16),C(-2;6).ặ ẳ ể
a/ Ch ng minh A, B, C là ba đ nh c a tam giác.ứ ỉ ủ
b/ Tìm D đ t giác ABCD là hình bình hành.ể ứ
c/ Ch ng minh tam giác ABC vuông. Tính di n tích c a tam giác ABC. ứ ệ ủ
................H t.................ế
Tr ng THPT Trà Cúườ
T Toán ổ
Đ Chính Th c ề ứ
Đ Ki m Tra HK I ề ể - Năm h c : 2013-2014ọ
Môn : Toán – Kh i 10ố
Th i gian : 120 phút ( Không k th i gian phát đ )ờ ể ờ ề
II. ĐÁP ÁN:
Đáp án T.Đ Đáp án T.Đ
Bài 1:
2
/ 2 2a y x x= − + +
+ TXĐ: D=R.
+ Tr c đ i x ng ụ ố ứ
1.x=
+Đ nh I(1;3).ỉ
+a=-1<0 =>hàm s ĐB trênố
kho ng ả
( ;1),−
NB trên kho ngả
(1; ).+
x
−
1
.+
y
3
−
−
Đ th :ồ ị
x
-1 0 1 2 3
y
-1 2 3 2 -1
b) Ph ng trình hoành đ giaoươ ộ
đi m gi a (P) và (d).ể ữ
2
2
2 2 5 4
3 2 0.
1 1
2 6
x x x
x x
x y
x y
− + + = +
− − − =�
= − => = −
= − => = −
V y giao đi m c n tìm là: ậ ể ầ
A(-1;-1), B(-2;-6).
Bài 2:
a/
ĐK:
0.2
5
0.2
5
0.2
5
0.2
5
0.5
0.2
5
Bài 3:
2
2
/ 7 10 1 3
7 10 3 1
a x x x
x x x
− + + =
− + = −�
1
3.
2 2
7 10 (3 1)
x
x x x
− + = −
( )
1
3
2
8 9 0
1
3
1 ( )
9
8l
x
x x
x
x n
x
+ − =
=
−
=
V y: T p nghi m: S={1}.ậ ậ ệ
b/
pt
3
2
(3 1)(2 4) (6 1)( 3)
x
x
x x x x
−
+ + = + −
3
2
7( )
31
x
x
x n
−۹
−
=
V y: T p nghi m ậ ậ ệ
-7
{ }
31
S=
.
2 3 13
/7 4 2
x y
cx y
− =
+ =
8 12 52
21 12 6
x y
x y
− =
+ =
0.25
0.25
0.25
0.25
0.25
0.25
0.25
2
2
4 0
3 0
4
3
2
3
x
x
x
x
x
x
−
−
− −
b/
1 0
2 0
x
x
− >
−
1
2
x
x
>
1 2x<� �
0.2
5
0.2
5
0.2
5
0.2
5
0.2
5
0.2
5
0.2
5
2
2.2 3 13
x
y
=
− =
2
3
x
y
=
= −
0.25
Bài 4:
(2 1) 5 0.m x x− + + =
(2 1) 5 0x m m+ − + =�
BL:
1
2
m−
thì pt đã cho có nghi mệ
duy nh t: ấ
5
2 1
m
xm
−
=+
.
1
2
m= −
thì pt thành
11
0 0
2
x+ =
. =>
pt vô nghi m.ệ
K t lu n:ế ậ
1
2
m −
thì t p nghi mậ ệ
0.2
5
0.2
5
0.2
5
0.2
Bài 5:
2(2 1) 5 0mx m x m− + + − =
( ; (2 1); 5)a m b m c m= = − + = −
Tính:
2
2
4
(2 1) 4 .( 5)
24 1
b ac
m m m
m
∆ = −
= + − −
= +
Đ pt có 2 nghi m phân bi t thìể ệ ệ
0
0
0
0
1
24 1 0 24
a
m
m
mm
∆ >
� �
� � −
+ > >
0.25
0.25
m-5
{ }.
2m+1
S=
1
2
m= −
thì t p nghi m ậ ệ
.S
φ
=
5V y ậ
1
( ; ) \{0}.
24
m− +� �
thì pt đã cho có
hai nghi m phân bi t.ệ ệ 0.25
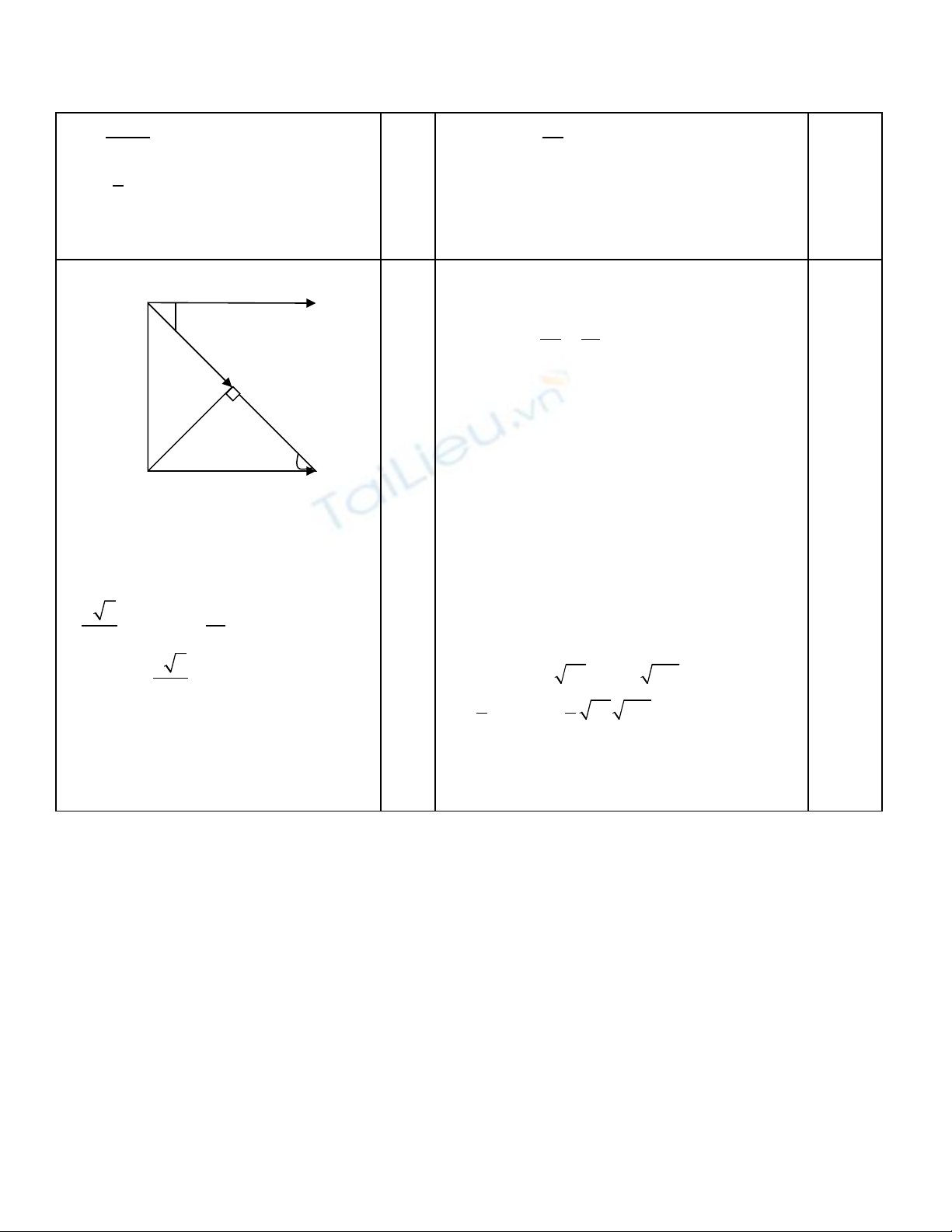
Bài 6:
A A’
H
450
B C
a/
0
( , ) ( , AA') 45 .AH BC AH= =
uuur uuur uuur uuur
b/
2
0
. . . os(AH, )
2. . os45 .
2 2
AH BC AH BC c BC
a a
a c
=
= =
uuur uuur uuur uuur
(có
a 2 .
2
AH =
)
0.2
5
0.2
5
0.2
5
0.2
5
0.2
5
Bài 7: A(3;4), B(2;16),C(-2;6).
a)
( 1;12), ( 5; 2).AB AC= − = −
uuur uuur
L p t s : ậ ỉ ố
1 12
5 2
−
−
=>
,AB AC
uuur uuur
không cùng ph ng.ươ
=> A, B, C là ba đ nh c a tam giác.ỉ ủ
b)
Do t giác ABCD là hình bình hành nênứ
AD BC=
uuuur uuuur
3 4 1
4 10 6
x x
y y
− = − = −
� �
� �
� �
− = − = −
� �
V y D(-1;- 6)ậ
b)
( 4; 10),BC = − −
uuur
. ( 5).( 4) 2( 10) 0.AC BC = − − + − =
uuur uuur
V y tam giác ABC vuông t i C.ậ ạ
* Tính
29.AC =
116.BC =
1 1
. 29 116 29( ).
2 2
S AC BC dvdt= = =
0.25
0.25
0.25
0.25
0.25
0.25
0.25
GV so n đ ạ ề
Tr n Phú Vinhầ