TRƯỜNG THCS QUI ĐỨC
TỔ TOÁN
ĐỀ THAM KHẢO HỌC KÌ I NĂM HỌC 2023 –
2024
MÔN: TOÁN 9
Thời gian: 90 phút ( không kể thời gian giao đề)
Bài 1: (2,0 điểm) Rút gọn biểu thức:
3
a)2 180 48 80 0, 2 125
4

2
b) 2 7 8 2 7 
5 3 3 5 4 6 15
c) 15 5 1 2 5



Bài 2: (1,5 điểm) Cho hai đường thẳng: (d1): y = - x + 3, (d2): y =
3
2
x - 2
a) Vẽ (d1) và (d2) trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (d1) và (d2) bằng phép toán.
Bài 3: (0,75 điểm) Giải phương trình:
6
12x 4 75x 25 7 3x 1 30
5

Bài 4: (1,0 điểm) Một xe gắn máy chạy với vận tốc 50km/h từ A đến B. Gọi s (km) là quãng
đường gắn máy đi được trong thời gian t (giờ)
a) Hãy lập hàm số của s theo t
b) Nếu quãng đường AB dài 25000 m thì thời gian để xe máy đi hết quãng đường AB là bao
nhiêu?
Bài 5: (1,0 điểm) Thực hiện chương trình khuyến mãi “Ngày chủ nhật Vàng”, một cửa hàng
điện máy giảm giá 50% trên 1 ti-vi cho lô hàng ti-vi gồm 40 cái, giá bán lẻ trước đó
là 6500000 đồng/ cái. Đến trưa cùng ngày thì cửa hàng đã bán được 20 cái và cửa hàng quyết
định giảm thêm 10% nữa (so với giá đã giảm lần 1) cho số Ti-vi còn lại.
a. Số tiền cửa hàng đó thu được khi bán hết hết lô hàng ti-vi.
b. Biết rằng số vốn là 2850000 đồng/ cái ti-vi. Hỏi cửa hàng lời hay lỗ khi bán hết số hàng ti-vi
đó?
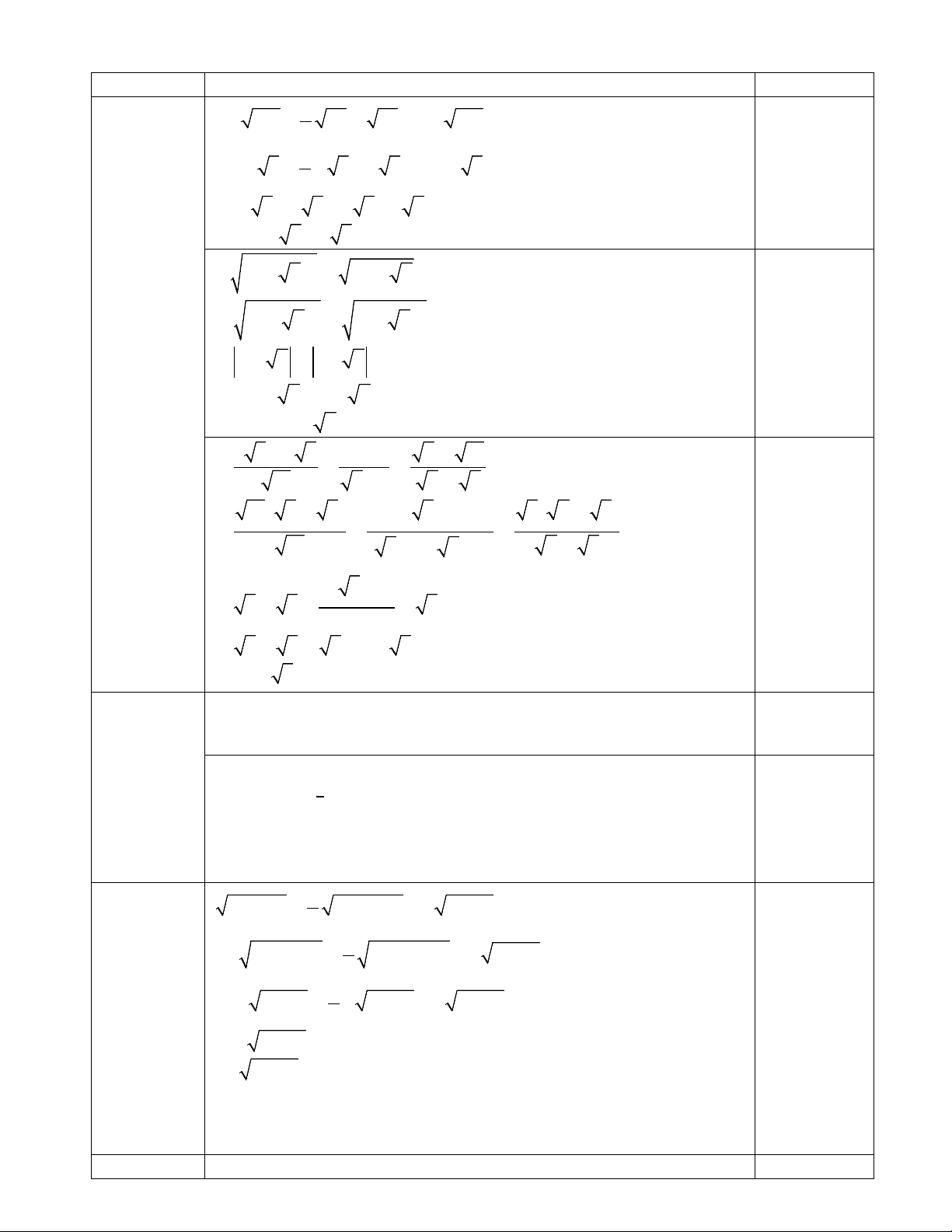
Bài 6: (0,75 điểm) Tính chiều cao của trụ cầu Cần Thơ so với mặt sông Hậu cho biết tại hai
điểm cách nhau 89 m trên mặt song người ta nhìn thấy đỉnh trụ cầu với góc nâng lần lượt là 400
và 300. (Làm tròn kết quả đến chữ số thập phân thứ nhất)
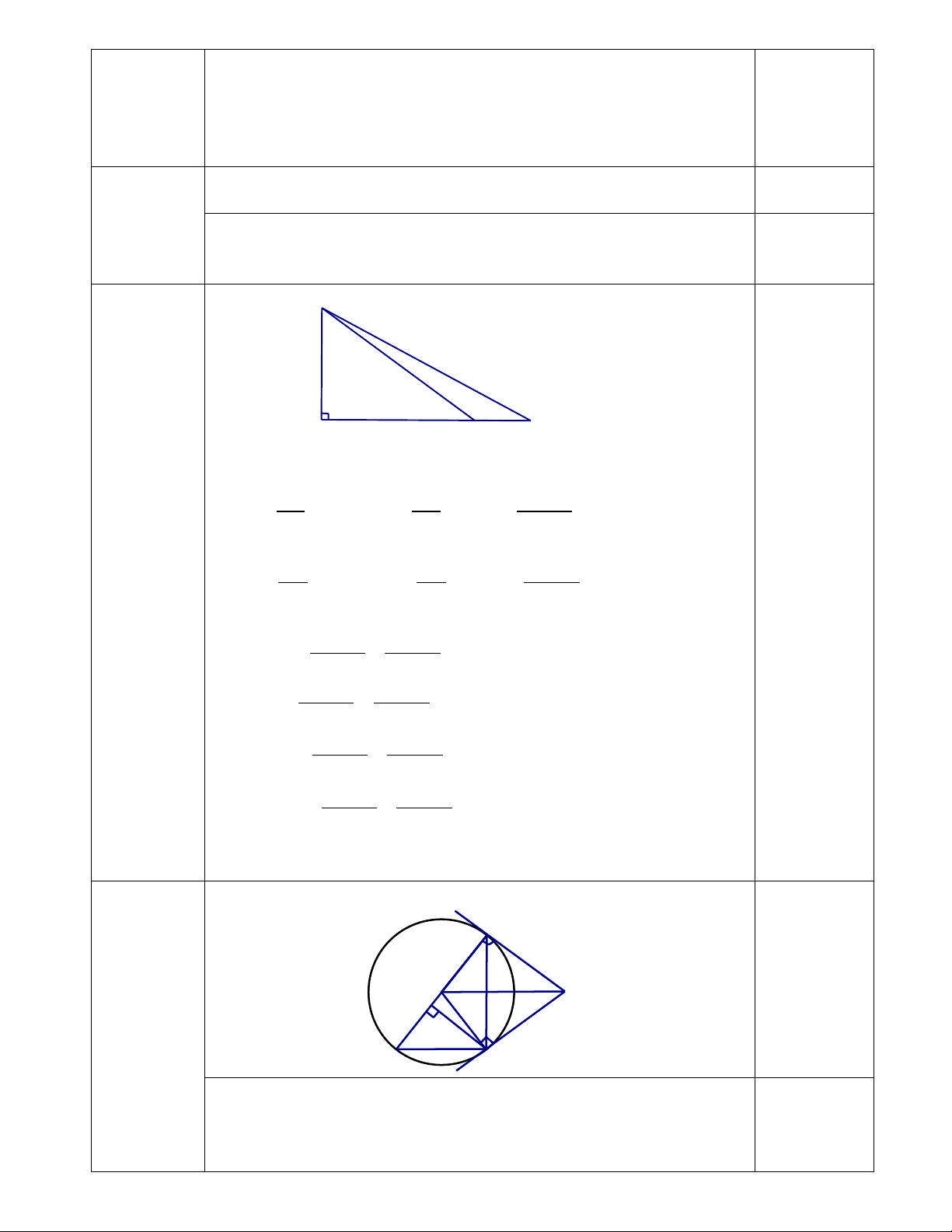
Bài 7: (3,0 điểm) Cho đường tròn (O;R = 6 cm) và điểm M ở ngoài đường tròn sao cho OM =
10 cm . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng
AB cắt OM tại K.
a) Chứng minh K là trung điểm của AB.
b) Tính MA, OK.
c) Kẻ đường kính AN của đường tròn (O). Kẻ BH vuông góc với AN tại H. Chứng minh MB.BN
= BH.MO.
- HẾT -
30
40
0
89 m
D
C
B
A
HƯỚNG DẪN CHẤM
BÀI
ĐÁP ÁN
ĐIỂM
Bài 1:
( 2,0 điểm)
3
a)2 180 48 80 0,2 125
4

3
2.6 5 .4 3 4 5 0, 2.5 5
4

125 33 45 15 
10 5 3 3
0,25 đ
0,25 đ
2
c) 2 7 8 2 7 
22
27 17 
2 71 7 
2 71 7
1 27
0,25 đ
0,25 đ
5 3 3 5 4 6 15
d) 15 5 1 2 5




15 5 3 4 5 1 3 2 5
15 2 5
51 51



451
53 3
4

5 3 51 3 
25 1
0,25 đ x 2
0,25 đ
0,25 đ
Bài 2
(1,5 điểm)
a) *BGT+Vẽ
( )
1
d
*BGT +Vẽ
( )
2
d
0,25 đ x 2
0,25 đ x 2
b) Phương trình hoành độ giao điểm
−𝑥𝑥 + 3 = 3
2
𝑥𝑥 − 2
x = 2
Thay x = 2 vào y = - x + 3 = - 2 + 3 = 1
Vậy giao điểm của (d1) và (d2) là (2; 1)
0,25 đ
0,25 đ
Bài 3
(0,75 điểm)
6
12x 4 75x 25 7 3x 1 30
5

6
4 3x 1 25 3x 1 7 3x 1 30
5

6
2 3x 1 .5 3x 1 7 3x 1 30
5

3 3x 1 30 
3x 1 10 
2
3x 1 10 
3x 99
x 33
0,25 đ
0,25 đ
0,25 đ
Bài 4
a) Hàm số: s = 50 t
0,25 đ
(1điểm)
b) Đổi 25000 m = 25 km
Thay s = 25 vào s = 50 t
Ta được: 25 = 50 t
t = 0,5
Vậy thời gian để xe máy đi hết quãng đường AB là 0,5 giờ
0,25 đ
0,25 đ
0,25 đ
Bài 5
(1điểm)
a)Số tiền cửa hàng đó thu được khi bán hết hết lô hàng ti-vi là:
20. 50%.6500000 + 90%. 20. 50%.6500000 = 123 500 000 (đồng)
0,5đ
b) Tiền vốn của 40 cái ti vi là: 40. 2 850 000 = 114 000 000 (đồng)
Số tiền cửa hàng lời sau khi bán hết 40 cái tivi là:
123 500 000 - 114 000 000 = 9 500 000(đồng)
0,25đ
0,25đ
Bài 6
(0,75 điểm)
ΔABD vuông tại A, nên
AB
tan C AC
0AB
tan 30 AC

0
AB
AC 1
tan 30

ΔABC vuông tại A, nên
AB
tan D AD
0AB
tan 40 AD

0
AB
AD 2
tan 40

Lấy (1) - (2) ta có:
00
AB AB
AC AD tan 30 tan 40

00
11
DC AB tan 30 tan 40



00
11
89 AB tan 30 tan 40



00
11
AB 89 : 164,7 m
tan 30 tan 40



Vậy chiều cao của trụ cầu Cần Thơ so với mặt sông Hậu là
khoảng 164,7 mét.
0,25 đ
0,25 đ
0,25 đ
Bài 7
( 3 điểm)
a) Chứng minh: K là trung điểm của AB.
MA = MB ( tính chất của tiếp tuyến )
OA= OB ( bán kính đường tròn)
Suy ra: OM là trung trực của AB
0,25 đ
0,25 đ
0,25 đ
H
N
K
B
A
M
O
30
0
40
0
89 m
D
C
B
A
Nên K là trung điểm của AB và
OA BC⊥
0,25 đ
b) Tính MA, OK.
+ ΔOAM vuông tại A, nên
OM2 = OA2 + AM2 (Pytago)
AM2 = 102 - 62
AM = 8 cm
+ ΔOAM vuông tại A, đường cao AK nên
OA2 = OK. OM
62 = OK. 10
OK = 3,6 cm
0,25đ
0,25đ
0,25đ
0,25 đ
c) Chứng minh MB.BN = BH.MO.
ΔANB có A, N, B thuộc (O) và AN là đường kính (gt)
ΔANB vuông tại B
Nên
NB AB
Mà
OM AB cmt
OM // NB
HNB AOM
(đồng vị)
Mà
AOM BOM
(2 tiếp tuyến cắt nhau)
HNB BOM
Xét ΔOBM và ΔNBM có:
HNB BOM
(cmt)
0
OBM NHB 90
Vậy ΔOBM đồng dạng ΔNBM (g - g)
MB MO
BH BN

Vậy MB.BN = BH.MO
0,25 đ
0,25 đ
0,25 đ
0,25 đ
HẾT