ĐỀ THI HỌC KÌ HỌC KÌ 2
Môn: Toán 8
Thời gian: 90 phút (Không kể thời gian phát đề)
ĐỀ SỐ 10
Bài 1. (2 điểm). Giải các phương trình sau:
a. 2x – 5 = x – 3
b. 3x(x – 1) + 2(x – 1) = 0
c.
1
4
1
1
1
1
2
x
x
x
x
x
Bài 2: (2 điểm).
a. Giải bất phương trình 3x – 2 ≤ 4 và biểu diễn tập nghiệm trên trục số.
b. Giải phương trình: 2x – 3 = x + 7.
Bài 3. (1,5 điểm).
a. Giải bất phương trình: 7
4
111
x
b. Cho a < b. Chứng minh: 3a – 2 < 3b + 5.
Bài 4: (2 điểm). Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm, đường cao
AH. Lấy D thuộc AH sao cho AD =
4
1AH. Đường thẳng d qua D song song với BC
cắt cạnh AB, AC tại E và F.
a. Chứng minh HBA HAC.
b. Tính EF.
c. Tính diện tích tam giác AEF.
Bài 5: (1,5 điểm).
Cho hình hộp chữ nhật ABCD.A’B’C’D’.
Biết AB = 4cm. AD = AA’ = 3cm.
a. Tính thể tích hình hộp chữ nhật.
b. Tính A’C.
Bài 6: (1 điểm)
Một người đi xe máy từ A đến B với vân tốc 40 km/h . Lúc về, người đó đi với
vận tốc 30 km/h, nên thời gian về nhiều hơn thời gian đi là 45 phút. Tính quãng
đường AB.
............................Hết............................
S
ĐÁP ÁN VÀ BIỂU ĐIỂM
Bài Nội dung Điểm
1
A 2x – 5 = x – 3
2x – x = -3 + 5
x = 2
Vậy tập nghiệm của phương trình là S = {2}
0,25
0,25
B
3x(x – 1) + 2(x – 1) = 0
(x – 1)(3x – 2) = 0
x – 1 = 0 hoặc 3x +2 = 0
x = 1 hoặc x =
3
2
Vậy tập nghiệm của phương trình là S = {1,
3
2
}
0,25
0,25
C
ĐK: x ≠ 1 và x ≠ -1.
1
4
1
1
1
1
2
x
x
x
x
x
1
4
1
)1(
1
)1(
22
2
2
2
x
x
x
x
x
Suy ra: (x + 1)2 – (x – 1)2 = 4
4x = 4 x=1
Vậy tập nghiệm của phương trình là S = {1}
0,25
0,25
2
A
3x – 2 ≤ 4
3x ≤ 6
x ≤ 2
Vậy tập nghiệm của bất phương trình là {x/ x ≤ 2}
0,5
0,25
0,25
B
2x – 3
= x + 7 (1)
+ Nếu 2x – 3 > 0  x >
2
3 2x – 3 = 2x – 3
(1) thành 2x – 3 = x + 7 x = 10 (TMĐK)
+ Nếu 2x – 3 < 0 x <
2
3 2x – 3 = 3 – 2x
(1) thành 3 – 2x = x + 7 x =
3
4
(TMĐK)
Vậy tập nghiệm của phương trình là: S = {10;
3
4
}
0,25
0,25
0,25
0,25
3
A 7
4
111
x 1 – 11x > -21 -11x > -22
x < 2. Nghiệm của bất phương trình là x < 2
0,25
0,25
b Ta có a < b
3a < 3b
3a – 2 < 3b – 2.
Mà: 3b – 2 < 3b + 5
Suy ra: 3a – 2 < 3b + 5.
0,5
0,25
0,25
]
0
4
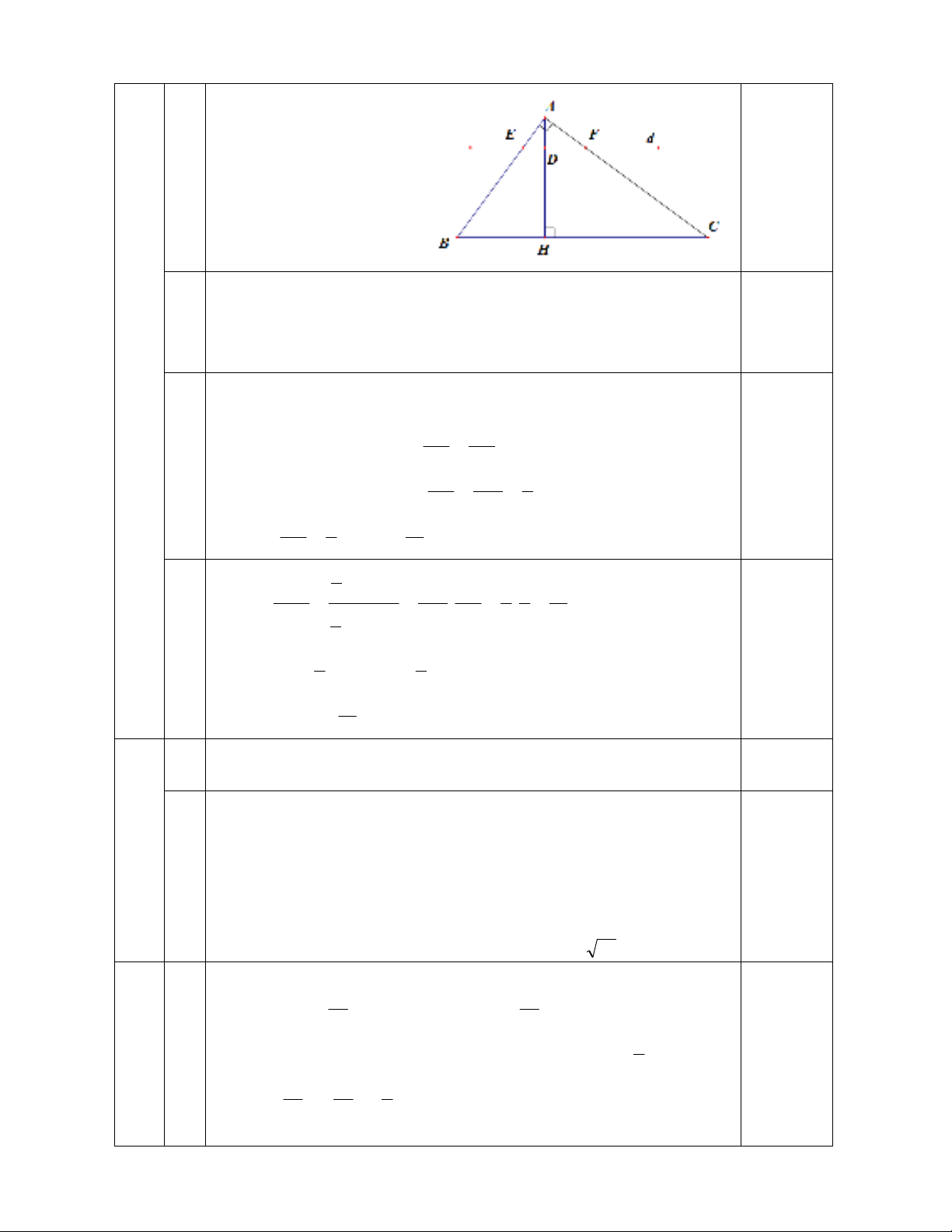
Vẽ hình đúng
0,5
a
HBA và
HAC có:
0
90
ˆˆ CHABHA
CAHB ˆ
ˆ(cùng phụ với góc C)
Suy ra: HBA HAC
0,25
0,25
b
Ta có:
ABC vuông tại A nên theo định lý Pitago ta có:
BC2 = 62 + 82 = 100 BC = 10cm
Mặt khác: EF // BC
BC
EF
AB
AE
ED // BH
4
1
AH
AD
AB
AE
Suy ra: cmEF
BC
EF 5,2
4
10
4
1
0,25
0,25
c
Ta có: 16
1
4
1
.
4
1
.
.
2
1
.
2
1
BC
EF
AH
AD
BCAH
EFAD
S
S
ABC
AEF
Mà SABC =
2
1AH.BC =
2
1.6.8 = 24 cm2
Suy ra: SAEF =
16
1.24 = 1,5 cm2
0,25
0,25
5
Thể tích hình hộp chữ nhật:
V = 4.3.3 = 36 cm3
0,5
Xét tam giác vuông ABC trong mp(ABCD).
Áp dụng định lý Pitago ta có:
AC2 = AB2 + BC2 = 42 + 32 = 25 AC = 5 cm
Mặt khác: AA’ mp(ABCD) nên AA’ AC
Xét tam giác vuông A’AC trong mp(AA’C’C).
Áp dụng định lý Pitago ta có:
A’C2 = AA’2 + AC2 = 32 + 52 = 34 A’C = 34 cm
0,5
0,25
0,25
6
Gọi x (km) là quãng đường AB.( ĐK: x > 0)
Thời gian đi:
40
x
(giờ). Thời gian về:
30
x
(giờ)
Vì thời gian về nhiều hơn thời gian đi là 45 phút =
3
4
giờ n
ên ta
có pt:
30
x
–
40
x
=
3
4
x = 90 (thỏa mãn điều kiện)
Vậy quãng đường AB là: 90 km
0,25
0,25
0,5
S
Mọi cách giải khác đúng vẫn đạt điểm tối đa
ĐỀ THI HỌC KÌ HỌC KÌ 2
Môn: Toán 8
Thời gian: 90 phút (Không kể thời gian phát đề)
ĐỀ SỐ 11
Câu 1: (2,25đ) Giải các phương trình sau:
a) 2x(x – 3) = (5x – 2)(x – 3)
b) xx 424
c)
)2(2
1
1
2
2
x
x
x
x
x
x.
Câu 2: (1,5đ) Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:
a) 3 – 2x ≥ 4.
b)
8
51
2
4
21 xx
.
Câu 3: (1,5đ)
Một người đi xe đạp từ A đến B với vận tốc trung bình 15km/h. Lúc về vì quá mệt nên
người đó chỉ đi với vận tốc trung bình 12km/h, cho nên thời gian về nhiều hơn thời gian đi
là 40 phút. Tính quãng đường AB.
Câu 4. (3,5đ)
Cho hình chữ nhật ABCD có AB = 12cm, BC = 9cm. Gọi H là chân đường vuông góc kẻ
từ A xuống BD.
a) Chứng minh ΔAHB ~ ΔBCD
b) Tính độ dài đoạn thẳng AH.
c) Tính diện tích tam giác AHB.
Câu 5: (1,25đ)
Cho hình lập phương ABCD.A'B'C'D' có AB = 5cm. Vẽ hình, tính diện tích toàn phần và
thể tích của hình lập phương đó.
---------------------------------------------