so clAo DUC vA nAo rAo
Q{rANG TRI
of cnfxu rmJc
@i cd 4 trang, gdm 50 cdu)
ruTNA TRA CU6I I(t TT L6P 12 THPT
NAM Hec zozo -zozt
nadx roAN
Thdi gian tdm bdi: 90 phlit (khdng M thdi gian pluit di)
Hq t6n: ........ SO b6o danh: Mfl da 003
Cflu 1: Cho hirn s6 y = f (*) fi6n tirc tr6n doqn [a;b). DiQn tich ,S cua hinh ph6ng eioi han boi dd fti hnm s6
!= f (x), trychoanhvihaidu&ngthang x=a, x=b (a<e) la
bbbb
A.. s= It(.)a". B. s= "lltt{la.. c. s=ll/(r)lrt. D. s= "[f'(*]a*.
CAu 2: Trong khOng giert Oxyz, vecto ndo sau d0y ld rnQt velto ph6p tuySn cira m{t ph["g c6 phucrng trinh
2n-y+32-1=0?
A. 4=(2;3;-1). 8.4=(z;-t;-t). C.r\=(z;r;t). D. ra=Q;*t;z).
Cffu 3: M6dun cria sd phuc z = 3 - i bing
^, 2.J1. B. Jm . c. 8 . D. 10.
C6u 4: I{q nguy0n hd.m cria ham sd f (x) = e' lir
A. e" +C. g. 4lnC. C. xe*-l +C. D" xe' +C.
x'rt
C0u 5: T'rong k-hdng gian Oxyz, cho hai di6rn l(-1;2;3), BQ;a;4). Trung di5m cua doqn thing AB cb to4
d0 ra
a. (1;3;o). B" (2;1;-3). c" (z;0;0)" D. (-z;-t;:).
CAu 6; Trongkh6ng gian Axyz, mfltc&u (S):x2 +y2 +z'-4x+6y*3=0 e6bdnkinhb[ng
a. J*si. B. dTo. c. 4. D. 16.
Cflu 7: 'frcng khdng gian Oxyz, vectc, nfro sau d6y ln m$t vectev chi phuong cria ducrng thang
x+1 v-2 z-2
A ' ----- = !--._: _'_-'/
3--35
A. 6 = (:;:;s'1. B. i = {t;*z;-z}. C. it =(*t;z;z). D. i =(:;-:;s}.
Cfiu 8: Cho hai s6 phr?c z, =l- 2i vit zz =3-4i. Iirn s6 ph&c z = zr-Zzz.
A. z=*5*10r. B. z=-2+2i C. z=4-Gi. I). z=-5+6i,
CAu 9: Chohai s6phric zt=5-4i vd zr=-3+i. Ph6nthucciras6phucw =zt*zrbing
A. *3. E. 2 " C. -2. D. 8.
Ciu 10: Cho hdm sd y=/(x) li0ntpc tr0n lR. vi a limQt s6 ducrng.'liong c6c khdng dinh sau, kh["g
dinh ndo ilting?
4
t. ).f (x)ax=a'.
CSu 11: Gqi a, vi z, lirhai nghiQm c{raphumrg titth 3zz -42+7 =0.Tinh P = zt
dx
r (*)
C.
0
dx
r(*)
B. I
a
1D. dx
irt.)
* zz,
2a
,|
A. P =L
^
J
L
B. P=-
a
J
1
c. p: --.
a
J
4
D. p - -"-.
^
J
Cfiu 12: Cho him sO 1(x)= r'. Khing dinh nio sau d6y dling?
. f 't, .tr' ? t - x' '
n. Jx'e=?*C. s. lx'ax=T"r. c. tx'ax=zx+C. t. lx'ax=x3 +c.
Cf,u 13: Cho him s6 y = /(x) c6 A6 tni nhu hinh v6. DiQn tich phAn gpch ch6o trong hinh bang
I
A. ^S=!t
-2
c. s=lf
0
(r)
(4
x
(4 +
dx.
dx
0
B. s=J,r
-2
0
D. s=[r
-2
/(4 x)
I
" Jr(
0
I
-lrt
0
*)e.
dx r ="ft;)
I
I
0
o
(dx. \ax dx.
Trang ll4 -MLAA OOI
I
Cflu 14: Trong kh6ng gian Ox-vz, tam ctra rnflt cAu (.9): (x- 3)' +(y+1)2 + (' -5)'= 5 c6 t9a d0 li
,t. (:;-1;s) B. (-:;r;-s)' c' (3;Ls)' n' (-:;-t;-s)'
cflu 15: Trong kh6ng gian oxyz, cho hai di€,m A(3;2;0), 8(1;4;3)' 'tqa d0 vecto 'qB h
A" (z;z;3). n. (*2;23)' c' (z;-z;-t)' o' (z;-z;3)'
Cffu 16; Trong rnflt phdng tqa d0 Oxy , di1m Al \-Z;S] bi6u di6n cho s6 phuc ndo sau ddy?
A. 5+2i. B. 2+5i. C. s*zi. D: .2-lf': 3
Cf,u 1?: Trong kh6ng gian Oxyz, cho hai di6m ,4(1;2;A),8(2;3;-l)' Phucrng trinh chinh tdc cira dudng
tfrArre AB liL
x-l v-2 z
A'-r =-t =1' x_2 y-3 _z+1 r
-=
v.
1 1 -1
8.4
x+1 y+2 *:1 = y*Z
')3
D. z
-i
B. 1 1 *1
Cffu 18: Trong kh6ng gian Oxyz, mat phang ndo duoi d6y di qua dir6m (z;*t;:)r
A.(Pr) :x-2y-22-2=0.
C.(P,) :x*Zy-22+2=4.
CAu L9: Tich Phdn
,
I1
(x+:)'dxblns
61
A. -.
J
B. (Pr):x-2Y+22-2=0.
D. (P,):x+2Y-22+2=0.
c" 51.
9
Cflu 20; Trong khdng gian Oryz, phuong trinh tham sO cira duong tha"e di qua tli6m ' (l-2;3) ve' c6 rnQt
vectrv chi phuong , = (O;*t;Z) ta
D. 61.
D. lzl= s.
[x=l l''=' [x=l+l
x"\y=-Z-t. Ir. lt=*z+t' t' l'=-2-t'
lz=l+2r lz=3+2t \z=3+2t
CAu 2i: Cho sO phirc z =3+2i' PhAn 6o cua sd phirc Z, hAYU
A.2. B.-zi. c'*2'
Ciu 22:Bi6t F(x) ld rnQt nguyeir hdm ctra hilrn sO f (*) = 2x (3 + 2 h x) vn i-
lx-t
,. 1, =-2-t.
I z =3+2t
!
D. 2'.
(1) = 3. Kha"g dinh nio sau
ddy dtng?
.a.. f(x) =Zte'+2x21nx'rl" B' f'(x) =2x' +-2x21nx*l'
C. i-(x) = 4x2 +2xz lnx. D' F(x) = 4x2 +2x21nx'-1'
cfiu23:Trongkhong gianoxyz'rnitciu ttrn I(2;*l;2) vddiqua M{2;a;\ c6phuungtdnhle
A. (x *2)'+(y+1)' +(z- 2)' =2' B" (x -2)7 +(y+1)' +(z--2)' =Ji'
C.(x +2)z +(y-1)' +(z+'2)'' =2" D'(r -2)'+(y+l)'-r(z*2)'=1'
Cffu 2,{: Gqri z, , z, Ld"hai nghiQm phr?c cua phuong tr\nh' 3zz - z +l=0 vA M 'N ta^ tuqt li hai di0m bi0u
di6n cua 211 z2 tr6n mflt phang tqa d0 Oxy' Tirth T = OM + ON '
Jr4 )
A"p=-'-. Y.P=i. c'P=*'
3 "" 3' 3D.P=+
Cflu 25: Cho s6 phrlc z = a * bi (a,b em) tfrOa m6n z + t+ 3i = zi'
A. S=-5. B. S=5. C' S=-3'
Cfiu 26: Trong kh6ng gian Oxyz, cho hai vectcv i1=(t;-t;Z)'i = (
hai vecto i va i1 co toa d0
-1. 1-z,l;-s). B. (-?;3;s). c' (z;-:;-s)'
Cfil_2l;Tinh mO<lun cua sO phtc z thda mtui z(1+i)+3t =l '
A. 14=.6. B. 14=-"6' c' lel=-s'
Tinh S =a*3b.
D. S=3.
2);L). Vect<r [i,i] tti"trc6 huong cua
u. (o;-3;1)"
Trang 214 -MLAA OO:
Ciu 28: Cho
A" /+28. B. 1= 6.
Cfru 29: Tim sd phtrc zbi6t r = (5 - Z;)(; +t).
f (*)e = -11 vcn a <c <b. Tinh / =
t(*)tu=tr7 vd
c
f
J
b
I
a
dx
/(r)
b
I
A. z =7 --3i .
Ciu 30: Cho 1=
A, .l =9.
z-3
B. z=-7-3i.
)d*=3. Khi d6 J =
B. -I = 18.
2
I
0[+y1x)*l]ax uang
C. I=*6.
C, z*7+3i.
C. J =6.
D. / = *28.
b" z=*7 +3i.
D. J=4.
Il. p=1"
2
D.3
(r
.f
2
i
0
Cflu 3l: Cho hinh phang (ff) gi6i h+n boi dO thi him s5 !=x2, truc hodnh vi hai dulng th*ng x=i,
x =2.euay hinh (H) quanh tryc iroanh ta dugc khOi trOn xoay c6 tne U"f, bhng (dvtt)
A.so. 8.21 . c. 1y D.ry
31' 2' - 5 3
Cfiu 32: Trong kh6ng gian Oryr, cho di6m M(l;Z;-a) ua duimg thiite d cb phuong trinh
x y+\ Phuung trinh cua m4t ph6ng di qua M vbwdng g6c vcri d li
r2-3
A. x+2y-32*1=0. B. x*-2y-32-7 =A. C. x-r2y*32*13=0. D. x+2y+32-1=0.
Ciu 33: Hg nguy6n hAm eria hdm sd "f (r) = sin2r ld
A. lcosZr+C.
2D. --l-.r* 2x+C.
2
B" -cos2x+C. C.2cosZx+C.
Cflu 34: Trong khdng gian Oxyz, cho ba diArn U(t;O;Z),lf(Z;t;O),f(O;1;:). M[t phAne (Aaff) c0
phu*mg tririh 1*:
A. 3x + ,v +22 *7 ={J. B. 3x '+ -v -rZz + 7 = 0' C, -2x+4y.+z=A. D. 5r*3Y+z*7 =0.
Cflu35: Cho sOphuc e =a+bi{a,b e [t) thoantan (i +i)z+22 =3+2r' Tinh P -a*b.
B, P *2. c. p=*1.
2
cin 36: c6 bao nhiOu so phrie z thira n$n lz -24i1= Zj'i vd {z- 1)(; +i) ra s6 thlrc?
A. 1. ts. 0. c. 2-
Cffu 37: I{g nguyOn him cria him sd f (x) = rilffi 6
n. l{7*r*c. n. 1(n'+l)tF+i+c" c. }(r'+11{k*1*s.
"'8' - 8' 8
cf,u 3S: Trong khOng gian oxy*2, hinh chiilu vu6ng g6c cua du&ng th1ng d:
phang (f ) : x *2y +22 -2 = 0 c6 phucrng trinh li
r[' +l * c.
A. P=-1.
A. xy-l z-2
D":
ti
x*t
2
vz*) trOn m4t
11
BC. x*4 vz+3 D. I= Y-l= z-2 .
2*1 1
I). 397
4
4l
Cfiu 39: Bi6t
937
1
_I *4 11 153
1r
aox
I
-
= alns +hlo|+ cln3 v6i a,b,clilcAc s6 nguv6n. MQnh dd ndo sau dfly clfing?
d r'*7x+12
A. a+3b+5c=0. B. a*3b*5c=*1. C- a*b*c=2. D. a.+b*c=*2.
Cflu 40: DiQn tich hinh pheng gi6i h?n boi cdc dulng cong y=-f +lLx vit y = -x2 bang
A. B. i1l
12
t2 C. 793
4
Ciu 41r Trong mat phf,ng tqa d0 Oxy , til.p hqp diAm bi6u di6n sd phrlc z thba mtu lz -Zil = lz(1+ 2;l U mgt
ducrng trdn. T6m vi ban kinh cria du&ng trdn d6 tin tuqt ta
R= S.
nu. l[0,-!"]. * =f
\.'2)' 2
o. ,[0,-]),*=,. n. {-!;o),n=,. c. /(-}'o),
Trang 314 -ME da 003
Cflu 422 Trong kh6ng gian O*yr, cho mfi phang (P):x+Zy+z+l=0 vi du6rng thang
'ttl+)=t-*2 =+.cql (g) Idmfltphing chindvdtaovoi (p) mQtg6c e,vucosp=f .rietr*g
1 1 -1 -'- \E / '' "'?' 'vr \r / ruvr tsur/ 6
.n =(z;n;c)(voi b < 0) la mQt vecto phdp tuy6n cta (Q).Iftdoe <tinh nio sau d6y thing?
A. b+c=*6. B. 6+ c=*24. C. b+c=2. D. b+ c=12.
CAu 43: Trongkhdng gian Oxyz,cho dudrngthang a,*.! =4=+ phuongtrinheuam{tph6ng di qua
2 | 2'-------c
U(Z;t;O) vdctuiaducrrlg thing d tit
A. 4x-6y*z+2=0. B. 4x -6y-z*2=A. C. x-Zy=Q. D. 2x+y+Zz-5=0.
ciu 44: Trong kh0ng gian oxyz, cho hai di6m A0;2;3), B{3;4;t). Gqi M(x;y;0) ld di6m thuQc mflr phing
(O"y) saocho A'IA+MB dqtgiittrinh6nh6t.pat T=x*y,kh6ngdinhniosaud6yrling?
(tz I
A. r e I 4;t i n. r'e (r;sl. c. (z;io). D. r e [r,9-l
\2 j ----\''-J' Yrr€1.''2]
c8u 45: Trong kh6ng gian (txyz, chc mht cAu (s):(x +2)2 +(y+l), +(z*2)z =16 vi hai di6rn
;(s;o;3), r(9;-3;a). Gqi (P), (8) l6nluqt ldhai matphlng ch*a AB vdti€p xirc voi (S) tpi M,N.
TirLh d0 dii do4n thflng n0l.
A. s. B. 9. c" 3. D.24
5 -- 5 '
Ciu 46: Ctro sO ph&c z th6a.ni&n iz*l+2il=lz+5ii vd t4t=iz+10. Girltd n-h6 nh6t cua l**l datduqc khi
w = s + bi (a,bei't). fmn p = u2 *h2.
A. --i8. B. 12.
Cfiu .11: Ciro hnm sO y = f {x) li0n
2
j[ f'(-) t x]e" dx = t, .{ (Z} = q, f (a)= 0 . Bi6t
0
do az +&2*c bing
A. 893 ngdnddng.
C" 4't6 ngdn ddng.
c. 128. D. 160.
tlic vh c6 deo hnm tr€n [O; Z] th6a m6n
lx
[ *f (r\ e" dx = ae"::c , v6i a,b,c li c6c s6 nguy6n. Khi
,b
A. 104. B" 146" c. 90. D.48.
Cf,u 48: Nguoi ta mu6n tr6ng mQt wcvn hoa c6m tti cAu trdn mQt aranh vucrn gicri hpn
brvi mdt dutmg par$o"l vd m$t nira d*ourg tron c6 ban kinh J2 m6t (nhu phAn tO dAm
tl?ng,linh,''.,8). Bi6t rang d6 Edng mgt iit vu6ng hoa cAn it nil6t zso ngdn ding.'s6
ti0n tdi thi0u dd tr6ng xong vubn hoa cAm. tu ciu gan bang flem trdn dOn ngan d6ng)
ll
2
A. F= 2&5
5
)\
B. P =-1.
a
J
B. 809ngdn ding.
D. 559 ngdnding.
C. P =T.
a
1D. P=4.
2
*t I z#
Ciu 49: frongkhdng gian Oxyz, chom{tcAu (S):x'+y'+22 -2x+6y-82+l=0. A,l? lahai di6mthuQc
(S) sao eho lB = 6' Gqi M (a;b;c) ld trung diOm cua do4n AB. Hdy tinh F = a +b + ctrong trulng hqp
a +2b +2c dqt gi6 tri iotr nh6t.
Cf;ur 50: Trong khdug giarr Oxyr, cho ba ducmg thang o,;=+= ry, b
^.x-5 y+7 z-3
L,_-=%=--*
123 ' Gqi d li duong th[ng song song v6 c ddng thoi cit trai ducmg thlng a vir b.
Duomg th[ng d di qua di,3m ndo sau d6y?
A. ,((t;*o;o). B. M(4;r;-t). c. H{*z;3;o\
*-* rufrr --* n. r(+;to;tz)
x+2 y-3 Z
1-32'
Trang 414 -M6dA 003
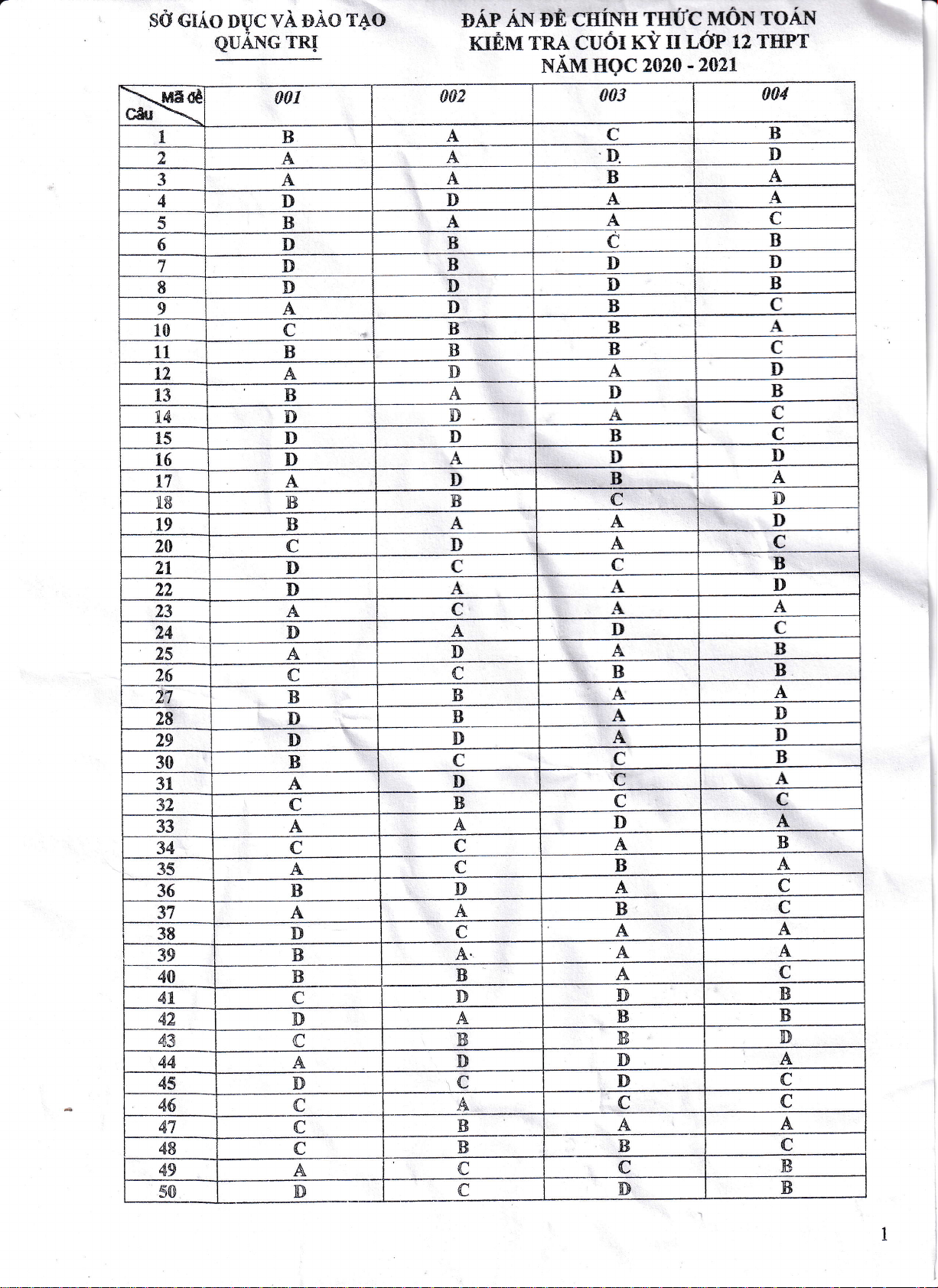
001 002 003 004
I
IBACE
4
AAA
nD. D
3AABA
4DDAA
3E.d l
l{ C
6DBfB
DIDD
IDDDB
9ADBC
10 rEBA
11 BBB
12 ADAD
B
13 BD
n4 Dts AC
IJ DDBC
16 DnDD
\7 ADBA
1l ii]
-u-o iE B(- D
19 ts AA.
20 \- T} AC
21 DCCB
a1 DAAD
,? dt rAA
24 DADt_
25 .4. n
|t AB
26 d- t- B
11 EEAA
28 Dts AD
,(} DDAD
30 BCCB
31 ADCA
tx rl ECC
33 .A l\ DA
34 (- CA. B
A
-r\ I.r
{.- BA
36 BD,d C
37 AAts C
38 D{1 AA
rl.
2(} E,& .A
40 RBA. C
41 q- sDts
42 D-A E
4.3 (t- Br}
ITD
44 ,A ts DA
43 ts s,- I} f,
45 CA- c- fi
47 d\
q- EAA
4E BBC
49 Ar1 u- m
_Ej
5S h
EN (- mB
ss craO Dvc
QUAN vA DAO TAO
G TRI EAP aX PN CHiNH THUC NTON TOAN
XTETU T'R,A CUOI ](V U LOP 12 THPT
NAM Hoc 2o2o -202r
C
D
1
\-mro€
CAr\
B
B