TR NG THCS NGHĨA TÂNƯỜ
Đ THI H C K II – NĂM H C 2019-2020Ề Ọ Ỳ Ọ
Môn: Toán l p 7 - Th i gian: 90 phútớ ờ
I.TR C NGHI MẮ Ệ (2 đi mể)
Tr l i câu h i b ng cách ghi l i ch cái đng tr c ph ng án đúngả ờ ỏ ằ ạ ữ ứ ướ ươ
Câu 1: Cho đn th c 5xơ ứ 2y. Đn th c nào sau đây đng d ng v i đn th c đã cho:ơ ứ ồ ạ ớ ơ ứ
A/ 5x2 B/ 5xy C/ - 7 x2y D/ 2xy2
Câu 2: Đa th c F(x) = xứ2 – x có các nghi m là: ệ
A/ x = 0 B/ x = 1 C/ x= 0 ; x = -1 ; D/ x = 0 ; x= 1
Câu 3. Cho tam giác ABC có AB = 7cm, BC = 5cm, CA = 10cm.
Kh ng đnh đúng là: ẳ ị
A.
CBA
; B.
BAC
;
C.
CAB
; D.
BCA
Câu 4. Cho tam giác ABC có trung tuy n AM và tr ng tâm G. T s ế ọ ỉ ố
AG
GM
là:
A.
3
1
; B.
2
1
; C.
4
1
; D.
3
2
II. T LU NỰ Ậ (8 đi mể):
Bài 1: (1,5 đi m)ể Th i gian gi i m t bài toán (tính theo phút) c a các b n h c sinhờ ả ộ ủ ạ ọ
l p 7 đc ghi l i nh sau :ớ ượ ạ ư
8 9 10 9 9 10 8 7 9 8
10 7 10 9 8 10 8 9 8 8
8 9 10 10 10 9 9 9 8 7
7 8 9 9 8 10 10 9 9 8
Hãy tính giá tr trung bình c a th i gian gi i bài toán trên.ị ủ ờ ả
Bài 2: (2 đi m): Cho 2 đa th c:ể ứ
1422
22363
32453
325342
xxxxxxxQ
xxxxxxxP
a. Thu g n và s p x p các đa th c trên theo lu th a gi m c a bi n.ọ ắ ế ứ ỹ ừ ả ủ ế
b. Tìm đa th c M(x) = P(x) + Q(x).ứ
c. Tính M(-2)
Bài 3: (1 đi m)ể
Tìm nghi m c a các đa th c sau:ệ ủ ứ
a.
4)1(2)( xxA
; b.
32)( 2 xxxB
;
Bài 3: (3,5 đi m) ể
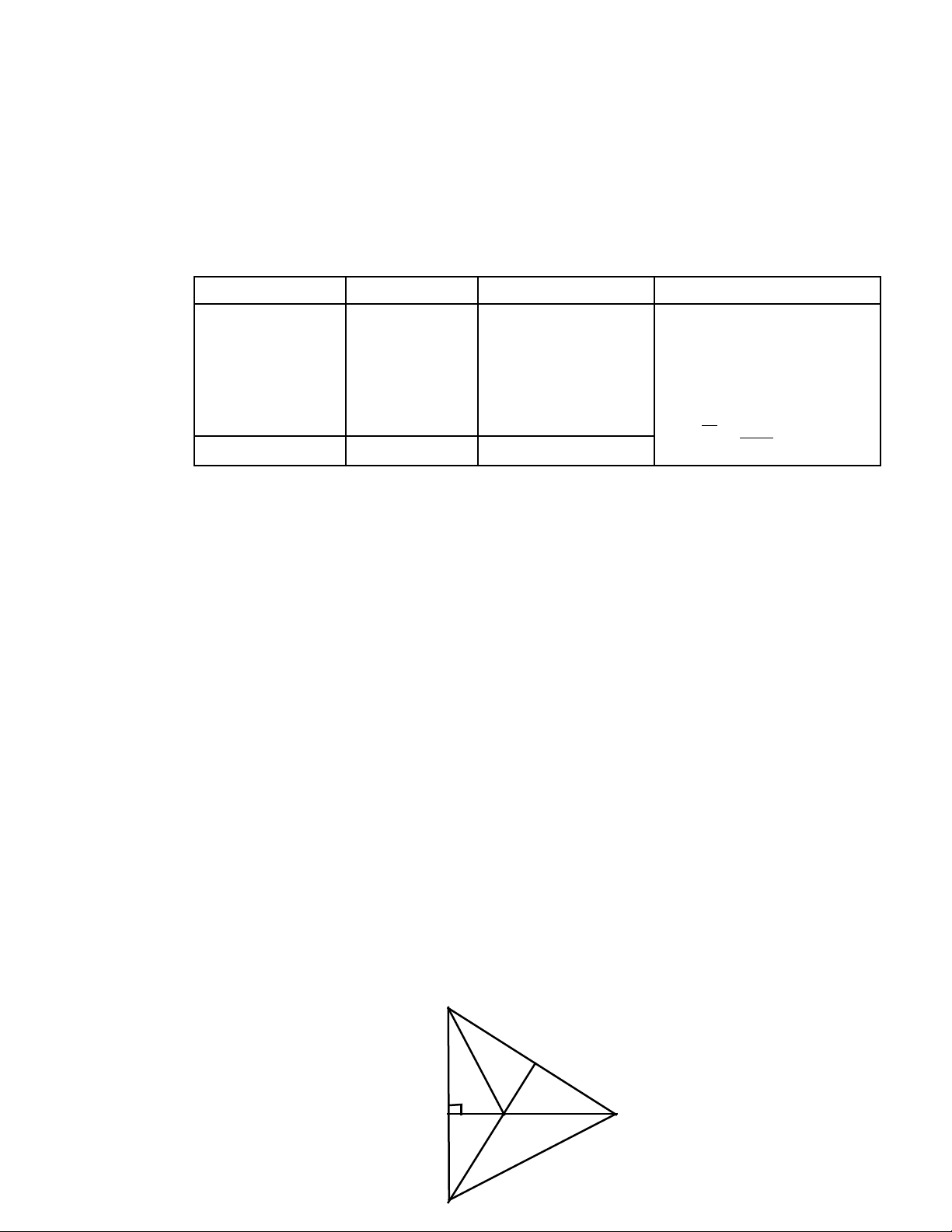
Cho tam giác ABC vuông A, đởng phân giác BE. Trên tia BC l y đi m H sao ườ ấ ể
cho BH = BA. G i K là giao đi m c a các đng th ng AB và EH.ọ ể ủ ườ ẳ
a. Ch ng minh: ứ
BHEBAE
.
b. Ch ng minh: AE < EC.ứ
c. Ch ng minh: BE ứ
CK.
d. Tam giác ABC c n thêm đi u ki n gì thì tam giác BKC đu.ầ ề ệ ề
ĐÁP ÁN TOÁN 7 H C KÌ IIỌ
I.Tr c nghi m (ắ ệ 2 đi mể): M i câu đúng ỗ(0,5 đi m)ể
1.C 2.D 3.D 4.B
II. T lu n (ự ậ 8 đi mể):
Bài 1 (1,5 đi m):ể
Th i gian(x)ờT n s (n)ầ ố Các tích (x.n)
7
8
9
10
4
12
14
10
28
96
126
100
N = 40 T ng : 350ổ
(có th HS dùng công th c đ tính, không c n l p b ng )ể ứ ể ầ ậ ả
Bài 2 (2 đi m):ể
a. Thu g n và s p x p:ọ ắ ế
P(x) = - 2x5 + x4 - x3 + 2x2 + 6 (0,5 đi m)ể
Q(x) = 2x5 - x4 + x3
14
2 xx
(0,5 đi m)ể
b. M(x) = P(x) + Q(x) = x2 + 4x + 5 (0,5 đi m)ể
c. M(-2) = 1 (0,5 đi m)ể
Bài 3: (1 đi m)ể
a. Đa th c A(x) có 1 nghi m là x = -1 ứ ệ (0,5 đi m)ể
b. Đa th c B(x) có 2 nghi m là x = 1; x = -3 ứ ệ (0,5 đi m)ể
Bài 3 (3,5 đi mể): V hình đúng 0,5 đi mẽ ể
a.Ch ng minh: ứ
ABE =
HBE (cgc) (1 đi m)ể
b.
CEH
có
HEECHCEEHCEHC
0
90
mà HE = AE
AEEC
. (1 đi m)ể
c.
0
90
BHEHBEABE
.
Xét
BCK
có
EKHCABCKHBKCA
;;
E là tr c tâm c a ự ủ
BCK
CKBE
. (0,5 đi m)ể
d.
ABC
có
0
60
B
thì tam giác BCK là tam giác đu.ề(0,5
đi m)ể
A
B
C
H
K
E