UBND HUYỆN XUYÊN MỘC
TRƯỜNG THCS HÒA HỘI
MA TRẬN ĐỀ KIỂM TRA HỌC KỲ II
MÔN : TOÁN 9
Ngày kiểm tra: 6 /05/ 2023
MA TRẬN ĐỀ KIỂM TRA HỌC KỲ II - MÔN TOÁN 9 NĂM HỌC 2022 - 2023
Cấp độ
Chủ đề
Nhận biết Thông hiểu Vận dụng Cộng
Cấp độ thấp Cấp độ cao
Giải phương trình và
hệ phương trình
- Giải phương trình bậc hai một ẩn.
- Giải hệ phương trình bậc nhất hai ẩn.
Số câu - Số điểm 2
2,0
2
2,0
Hàm số và đồ thị - Vẽ đồ thị (P): y = ax2 ; (d): y = ax+ b (a≠0).
- Bài toán về giao điểm của (d) và (P).
- Điểm thuộc (P) và (d).
- Tìm tham số chưa biết
Số câu - Số điểm 1 1
1,0 0,5
2
1,5
Ứng dụng phương
trình
- Phương trình qui về phương trình bậc hai;
- Giải bài toán bằng cách lập phương trình hoặc hệ
phương trình. - Vận dụng công thức nghiệm của
phương trình bậc hai; Sử dụng hệ thức Vi-et.
- Bài toán có tính chất thực tế
- Tìm GTLN, GTNN,…
Số câu - Số điểm 1
1,0
2
1,5
1
0,5
4
30
Góc với đường tròn - Kĩ năng vẽ hình;
- Định nghĩa, định lý tứ giác nội tiếp;
- Vận dụng các tính chất về quan hệ góc với đường tròn
để chứng minh;
- Hệ thức lượng trong tam giác vuông để chứng minh
và tính;
- Bài toán tổng hợp hình học.
Số câu - Số điểm
2(Vẽ hình 1 câu) 1
1,5 1,0
1
0,5
1
0,5
5
3,5
Tổng số câu -
Số điểm
5 3
4,0 3,0
3
2,0
2
1,0
13
10
UBND HUYỆN XUYÊN MỘC
TRƯỜNG THCS HÒA HỘI
ĐỀ CHÍNH THỨC
KIỂM TRA HỌC KỲ II
MÔN : TOÁN 9
Ngày kiểm tra: 6 / 05 / 2023
Bài 1: (3,0 điểm)
1) Giải phương trình: a) 3x2 + 2x – 8 = 0 b) x4 + 5x2 – 6 = 0
2) Giải hệ phương trình:
2 3
3 7
x y
x y
− =
+ =
Bài 2: (1,5 điểm) Cho parabol (P):
2
y x= −
và đường thẳng (d): y = 3x + 2
a) Vẽ parabol (P).
b) Tìm tọa độ các giao điểm của (P) và (d) bằng phép tính.
Bài 3: (1,5 điểm)
1) Một đoàn xe vận tải nhận chuyên chở 480 tấn hàng từ cảng về kho. Khi sắp khởi hành
được bổ sung thêm 3 xe nữa, nên mỗi xe chở chở ít hơn 8 tấn so với dự định. Hỏi đoàn
xe lúc đầu có bao nhiêu xe ? (biết năng suất mỗi xe chở như nhau).
1) Tìm giá trị của m để phương trình:
2
x mx m 1 0
− + − =
luôn có nghiệm
1 2
x ;x
sao cho
biểu thức
2 2
1 2 1 2
A x x x x
= − −
đạt GTLN
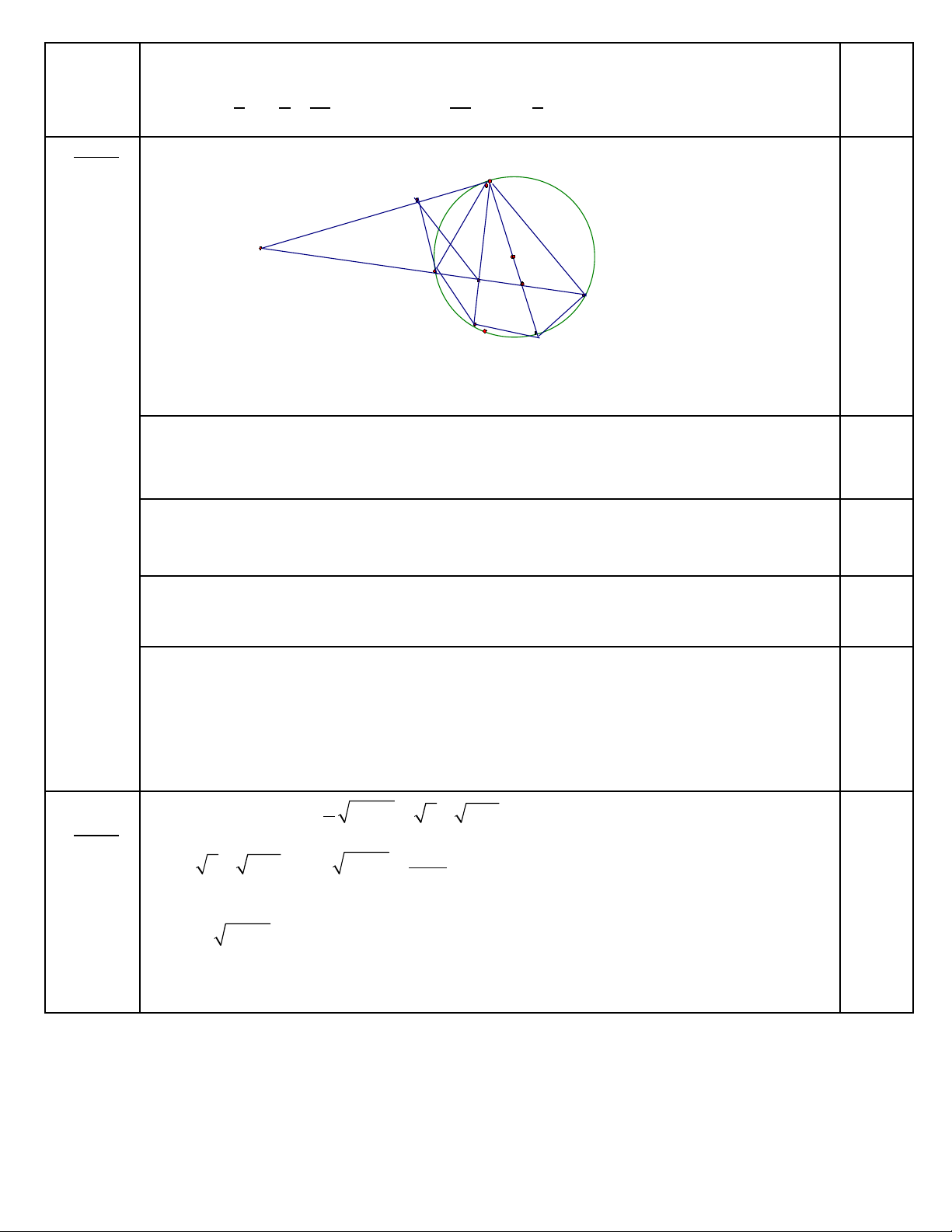
Bài 4: (3,5 điểm) Cho đường đường tròn (O;R) và một điểm A nằm ngoài (O). Dựng tiếp tuyến
AB với (O) ( B là tiếp điểm). Dựng cát tuyến AEF không đi qua O ( E nằm giữa A và F, B
thuộc cung lớn EF), kẻ dây cung BC vuông góc với AF tại D (D thuộc AF), kẻ EH vuộng góc
với AB (H thuộc AB).
a) Chứng minh: Tứ giác BDEH nội tiếp.
b) Chứng minh:
?
BFE =
?
HDE
c) Kẻ đường kính BI của (O) cắt EF tại G. Chứng minh: AD.AG = AE.AF.
d) Chứng minh: DB2 + DF2 + CE2 = 4R2.
Bài 5: (0,5 điểm) Giải phương trình
2
2
1 1
3x x x x+ − = + −
-----------------------------------Hết----------------------------------
UBND HUYỆN XUYÊN MỘC
TRƯỜNG THCS HÒA HỘI
HƯỚNG DẪN CHẤM KIỂM TRA HỌC KỲ II
MÔN : TOÁN 9
Ngày kiểm tra: 6/ 05 / 2023
Bài Nội dung Điểm
Bài 1
(3,0điểm
)
1)a) Lập
= 25
Phương trình có hai nghiệm
1 2
4; 2
3
x x= = −
0,5
0,25x2
b)x4 + 5x2 – 6 = 0
Đặt: x2 = t (t > 0), pt t2 + 5t – 6 = 0 , giải được
1 2
1; 6t t= = −
2
1
1 1 1t x x= = =
và KL nghiệm
0,5
0,5
2)
2 3 5 10 2
3 7 3 7 1
x y x x
x y x y y
− = = =


+ = + = =

, kết luận nghiệm 0,5-
0,25x2
Bài 2
(1,5điểm
)
1. a) Bảng giá trị
x -2 -1 0 1 2
y -4 -1 0 -1 -4
Đồ thị: (chính xác)
0,5
0,5
b)Lập được pt hoành độ giao điểm x2 + 3x + 2 = 0. Tìm đúng
1 2
1; 2x x= − = −
Tìm đúng
1 2
1; 4y y= − = −
. Tọa độ giao điểm: (-1;-4) và (-2; -4)
0,25
0,25
Bài 3
(1,5điểm
)
1)Go•i x(xe) sô• xe của đoàn xe lúc đầu( xZ, x>0)
sô• xe của đoàn xe thực tế la’ x + 3 (xe)
Sô• tấn hàng mô“i xe chở theo dự định là:
480
x
(tấn)
Sô• tấn hàng mô“i xe chở theo thư•c tê•:
480
3x+
(tấn)
Theo đê’ ba’i ta co• pt:
480 480
8
3x x
+ =
+
x2 + 3x – 180 = 0
12
15( )
x
x l
=
= −
Vâ•y Đoàn xe lúc đầu có 12 xe
0,25
0,25
0,25
0,25
2)Phương trình có hai nghiệm
( )
2
2
1 2
; 4 4 2 0x x m m m
∆ = − + = −
Với mọi giá trị của m.
Áp dụng Vi-ét:
1 2
1 2
1
x x m
x x m
+ =
= −
0,25
( )
2
2 2
1 2 1 2 1 2 1 2
2
3
3 3 3 3 3
( )
2 4 4 4 2
A x x x x x x x x
A m GTLN A m
= − − = − + +
− −
= − − − = =
0,25
Bài 4
(3,5điểm
)
0,5
a)Ta có:
ﾷ ﾷ
0 0
= 90 ; 90BDE BHE =
suy ra :
ﾷ ﾷ
0
180BDE BHE+ =
(tổng 2 góc đối)
tứ giác BDEH nội tiếp
0,25x2
0,25
025
b)Tứ giác BDEH nội tiếp, suy ra
ﾷ
ﾷ
EDH EBH=
(cùng chắn cung EH) và
ﾷ
ﾷ
EBH BFE=
(cùng chắn cung EB)
Suy ra
ﾷ
ﾷ
EDH BFE=
.
0,25x2
0,5
c)
∆
ABG vuộng tại B, Đường cao BD, suy ra: AD.AG = AB2 (HTL).
C/m
∆
AEB đồng dạng với
∆
ABF, suy ra: AE.AF = AB2
Suy ra: AD.AG = AE.AF
0,25
0,25
d)Ta có: DB2 + DF2 = BF2 (Pitago).
Suy ra: DB2 + DF2 + EC2 = BF2 + EC2 (1)
Ta có: CI song song với EF (cùng vuông góc với BC), suy ra
ﾷ
ﾷ
EC FI=
, suy ra
EC = FI (2)
Mà: BF2 + FI2 = BI2 = 4R2 (Pitago) (3)
Từ (1); (2) và (3), suy ra đpcm
0,25
0,25
Bài 5
(0,5điểm
)
Giải phương trình
2
2
1 1
3x x x x+ − = + −
Đặt:
( )
2
2
1
12
t
x x t x x −
+ − = − = ∗
Thay vào được pt: t2 – 3t + 2 = 0, suy ra
1 2
1; 2t t= =
( )
2
1
1 0 1 0 0; 1t x x x x x x= − = − = = =
2
2
2 4 4 9 0t x x= − + =
. Phương trình vô nghiệm
Vậy pt đã cho có hai nghiệm
1 2
0; 1x x= =
0,25
0,25
Lưu ý: HS có thể trình bày cách giải khác, giám khảo cân đối cho điểm.
_E _D
_F
_H
_I
_C
_B
_A _O
_G