1
Cấp độ
Chủ đề Nhận biết Thông hiểu Vận dụng Cộng
Cấp độ thấp Cấp độ cao
1. Đại số –
Chương III: Hệ
phương trình
bậc nhất hai ẩn.
Giải hệ phương trình bậc
nhất hai ẩn dạng đơn giản.
Số câu
Số điểm
Tỉ lệ %
1
1,0
10%
1
1,0
10%
2. Đại số –
Chương IV:
Hàm số y = ax2
(a ≠ 0). Phương
trình bậc hai
một ẩn.
- Giải phương trình bậc hai một ẩn (dạng đơn giản) bằng cách
tính nhẩm hoặc dùng công thức nghiệm.
- Vẽ đồ thị hàm số y = ax2 (a ≠ 0) với giá trị bằng số của a.
- Bài toán liên quan đến giao điểm của parabol và đường thẳng.
- Vận dụng linh hoạt hệ thức Vi-et, công thức nghiệm của
phương trình bậc hai.
- Giải phương trình quy về phương trình bậc hai, quy về
phương trình bậc nhất.
- Giải được bài toán bằng cách lập phương trình bậc hai một ẩn
(hoặc hệ phương trình bậc nhất hai ẩn).
Số câu
Số điểm
Tỉ lệ %
3
2,5
25%
2
2,5
25%
1
0,5
5%
6
5,5
55%
3. Hình học –
Chương III: Góc
và đường tròn.
- Vẽ hình đúng theo giả thiết bài toán.
- Vận dụng tính chất các loại góc có liên quan đến đường tròn,
các kiến thức về tứ giác nội tiếp để chứng minh các đặc tính
hình học, chứng minh tứ giác nội tiếp được đường tròn.
- Vận dụng linh hoạt các tính chất về góc và đường tròn, tứ
giác nội tiếp để làm bài tập nâng cao.
Số câu
Số điểm
Tỉ lệ %
3
2,25
22,5%
1
0,75
7,5%
1
0,5
5%
5
3,5
35%
Tổng số câu
Tổng số điểm
Tỉ lệ %
7
5,75
57,5%
3
3,25
32,5%
2
1,0
10%
12
10
100%
PHÒNG GIÁO DỤC ĐÀO TẠO
HUYỆN LONG ĐIỀN
TRƯỜNG THCS NGUYỄN HUỆ
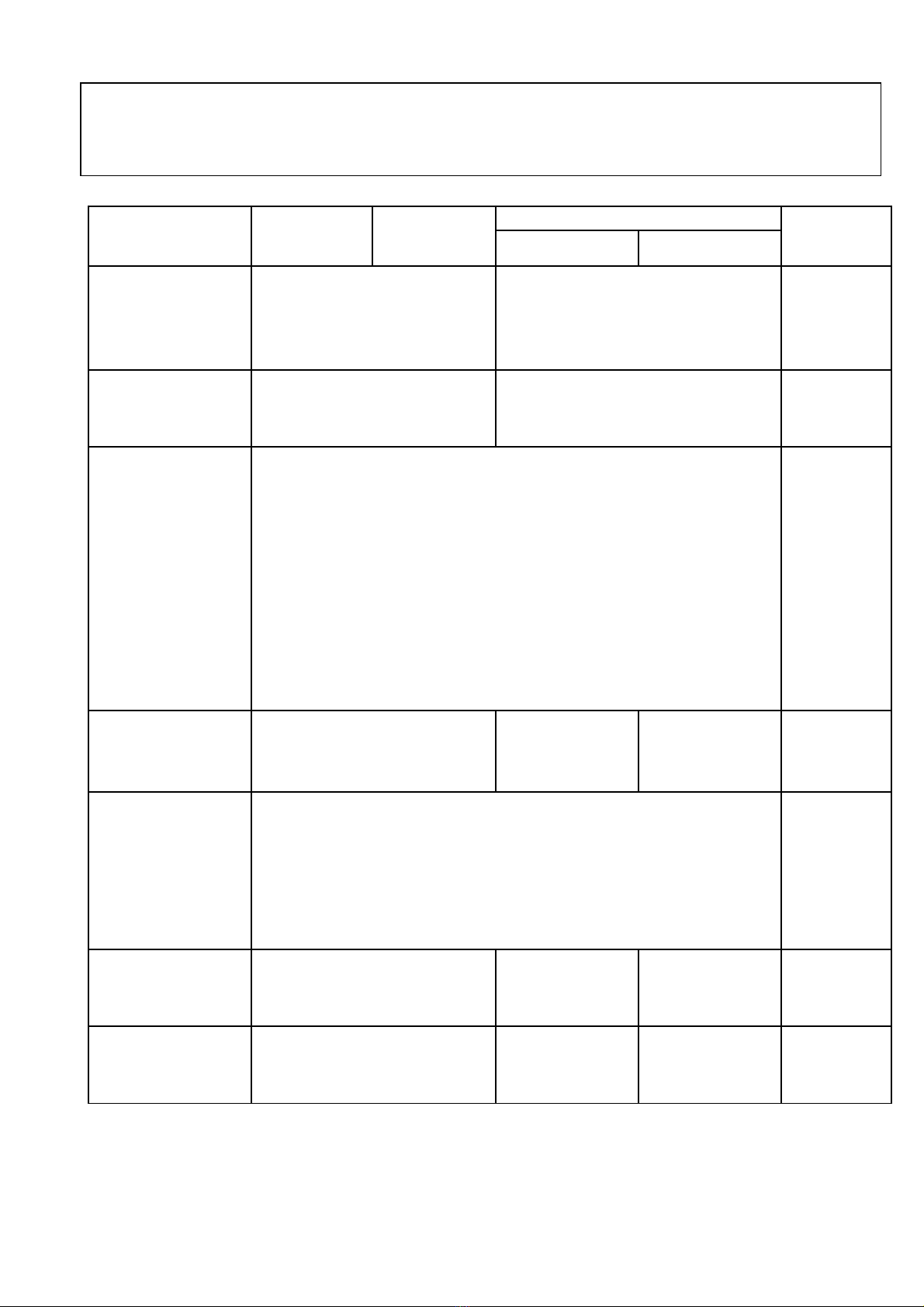
MA TRẬN KIỂM TRA CUỐI HỌC KÌ II NH 2022 – 2023
MÔN : TOÁN 9
Thời gian : 90 phút (không kể thời gian phát đề)
2
BẢNG MÔ TẢ ĐỀ KIỂM TRA CUỐI KÌ II
MÔN : TOÁN 9

Bài 1: (2,75 điểm)
a) Giải hệ phương trình.
b) Giải phương trình bậc 2.
c) Giải phương trình trùng phương.
Bài 2: (1,75 điểm) Cho Parabol (P) và đường thẳng (d)
a) Vẽ Parabol (P).
b) Tìm m để đường thẳng
( )d
cắt parabol
( )P
tại hai điểm phân biệt thỏa mãn điều kiện.
Bài 3: (1,25 điểm)
Dạng: Một mảnh đất hình chữ nhật có chiều dài hơn chiều rộng 7 m và có diện tích 800 m2.
Tìm chiều dài và chiều rộng của mảnh đất.
Bài 4: (0,75 điểm)
Dạng: Giá bán một cái bánh cùng loại ở hai cửa hàng A và B đều là 15000 đồng, nhưng mỗi
cửa hàng áp dụng hình thức khuyến mãi khác nhau.
Bài 5: (3,5 điểm)
Cho tam giác nhọn ABC có AB < AC và nội tiếp đường tròn tâm O. ...
a. Chứng minh: Tứ giác nội tiếp.
b. Chứng minh: Tia phân giác.
c. Chứng minh:
... ...
⊥
.
d. Chứng minh: Trực tâm của .
----------------- HẾT -----------------
3
(Đề thi gồm có 2 trang)
Bài 1: (2,75 điểm) Giải các phương trình và hệ phương trình sau:
a)
2 3 2
5 12
x y
x y
− =
+ = −
b)
2
2 15 0x x+ − =
c)
− − =
4 2
3x 7x 20 0
Bài 2: (1,75 điểm) Cho Parabol (P):
2
1
2
y x
=
và đường thẳng (d): y = x + m.
a) Vẽ parabol (P).
b) Tìm m để đường thẳng
( )d
cắt parabol
( )P
tại hai điểm phân biệt có hoành độ lần
lượt là
1 2
,x x
thỏa mãn
.
Bài 3: (1,25 điểm)
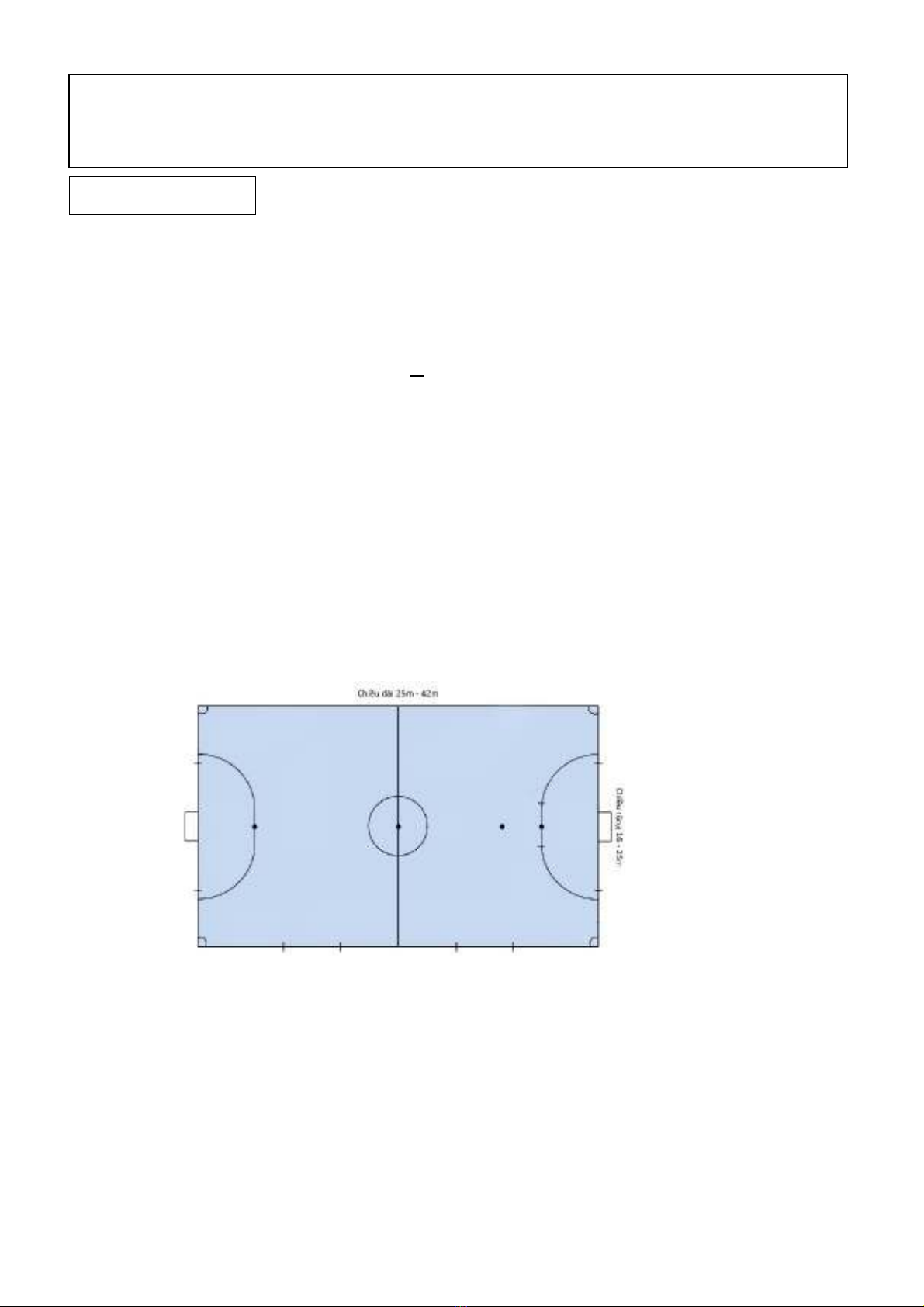
Theo quy định về sân bóng đá cỏ nhân tạo mini 5 người thì: “Sân hình chữ nhật, trong mọi
trường hợp, kích thước chiều dọc sân phải lớn hơn kích thước chiều ngang sân. Chiều
ngang tối đa là 25m và tối thiểu là 15m, chiều dọc tối đa là 42m và tối thiểu là 25m”. Thực
hiện đúng quy định kích thước sân 5 người là điều quan trọng để quản lý sân bóng và việc thi
đấu của các cầu thủ.
(Lưu ý: Học sinh không phải vẽ hình vào bài làm)
Sân bóng đá mini cỏ nhân tạo Minh Đạm có chiều dọc dài hơn chiều ngang 22m, diện tích
sân là 779m2. Hỏi kích thước sân này có đạt tiêu chuẩn đã quy định hay không ?
Bài 4: (0,75 điểm)
Sau buổi sinh hoạt ngoại khóa, nhóm bạn của Trang rủ nhau đi ăn kem ở một quán gần trường.
Do quán mới khai trương nên có khuyến mãi, bắt đầu từ ly thứ 5 giá mỗi ly kem được giảm
1500 đồng so với giá ban đầu. Nhóm của Trang mua 9 ly kem với số tiền là 154500 đồng. Hỏi
giá của một ly kem ban đầu ?
PHÒNG GIÁO DỤC ĐÀO TẠO
HUYỆN LONG ĐIỀN
TRƯỜNG THCS NGUYỄN HUỆ
ĐỀ KIỂM TRA CUỐI HỌC KÌ II NĂM HỌC 2022 – 2023
MÔN : TOÁN 9
Thời gian : 90 phút (không kể thời gian phát đề)
ĐỀ CHÍNH THỨC
4
Bài 5: (3,5 điểm)
Cho tam giác nhọn ABC có AB < AC và nội tiếp đường tròn tâm O. Đường cao AD của
ABC
∆
kéo
dài cắt (O) tại E (E khác A). Gọi F là hình chiếu của E trên AC. Tia FD cắt đường thẳng AB tại I.
a. Chứng minh: Tứ giác EDFC là tứ giác nội tiếp.
b. Chứng minh: EA là tia phân giác của góc BEF.
c. Chứng minh:
EI AB
⊥
.
d. Gọi M là điểm đối xứng của E qua AB, N là điểm đối xứng của E qua AC, MN cắt AD tại H. Chứng
minh H là trực tâm của ABC.
----------------- HẾT -----------------
Thí sinh không được sử dụng tài liệu. Giáo viên coi thi không giải thích gì thêm.
Người soạn đề
Phan Trọng Thảo
5
Bài Nội dung Điểm
Bài 1
(2,75đ
)
2x -3y = 2
)5x + y = -12
2x -3y = 2 17x = -34
15x +3y = -36 5x + y = -12
a
0,25 x 2
x = -2 x = -2
y = -5x -12 y = -2
Vậy nghiệm của hệ phương trình là:
=−
=−
x 2
y 2
- HS giải đúng HPT nhưng không kết luận vẫn cho tròn điểm.
- Nếu HS chỉ bấm máy tính cho ra nghiệm thì chỉ cho cả bài 0,25đ
0,25 x 2
b)
2
2 15 0x x+ − =
Ta có
1 4.2.( 15) 121∆ = − − =
0,25
Phương trình có 2 nghiệm:
1 2
5
3 à 2
x v x
= − =
(Nếu HS chỉ bấm máy tính cho ra 2 nghiệm thì chỉ cho cả bài 0,25 đ)
0,25 x 2
c)
− − =
4 2
3x 7x 20 0 (1)
Đặt
( )
2
x t t 0=
, PT (1) trở thành:
− − =
2
3t 7t 20 0 (2)
0,25
PT (2) có hai nghiệm
=
1
t 4
(nhận);
−
=
2
5
t3
(loại) 0,25
Với
= = =
2
t 4 x 4 x 2
0,25
Vậy PT (1) có hai nghiệm
= =−x 2;x 2
0,25
Bài 2:
(1,75đ
)
a) - Lập đúng 5 điểm trên bảng giá trị.
- Vẽ đúng đồ thị.
0,5
0,25
b) Phương trình hoành độ giao điểm:
2 2
12 2 0
2x x m x x m= + − − =
0,25
Ta có
' 1 2m
∆ = +
.
Pt có 2 nghiệm phân biệt
1 2
,x x
khi
1
' 0 2
m∆ > > −
(*) 0,25
Hệ thức Vi-ét
1 2
1 2
2
. 2
x x
x x m
+ =
= −
0,25
( )
2
2 2
1 2 1 2 1 2
5 2 5x x m x x x x m+ = + − =
4 4 5 4m m m + = =
(thỏa đk (*) 0,25
Bài 3:
(1,25đ
)
Gọi chiều ngang sân là x (m), điều kiện x > 0. 0,25
Suy ra chiều dọc sân bóng là x + 22 (m).
Vì sân bóng hình chữ nhật có diện tích 779m2, nên ta có phương trình: 0,25
PHÒNG GIÁO DỤC ĐÀO TẠO
HUYỆN LONG ĐIỀN
TRƯỜNG THCS NGUYỄN HUỆ
ĐÁP ÁN KIỂM TRA CUỐI HỌC KÌ II NH 2022 – 2023
MÔN : TOÁN 9
Thời gian : 90 phút (không kể thời gian phát đề)