UBND TỈNH THÁI NGUYÊN
SỞ GD&ĐT CỘNG HÒA XÃ HỘI CHỦ NGHĨA VIỆT NAM
Độc lập - Tự do - Hạnh phúc
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH
LỚP 12 - MÔN: VẬT LÍ – Năm học 2011 - 2012
Thời gian: 180 phút - (Không kể thời gian giao đề)
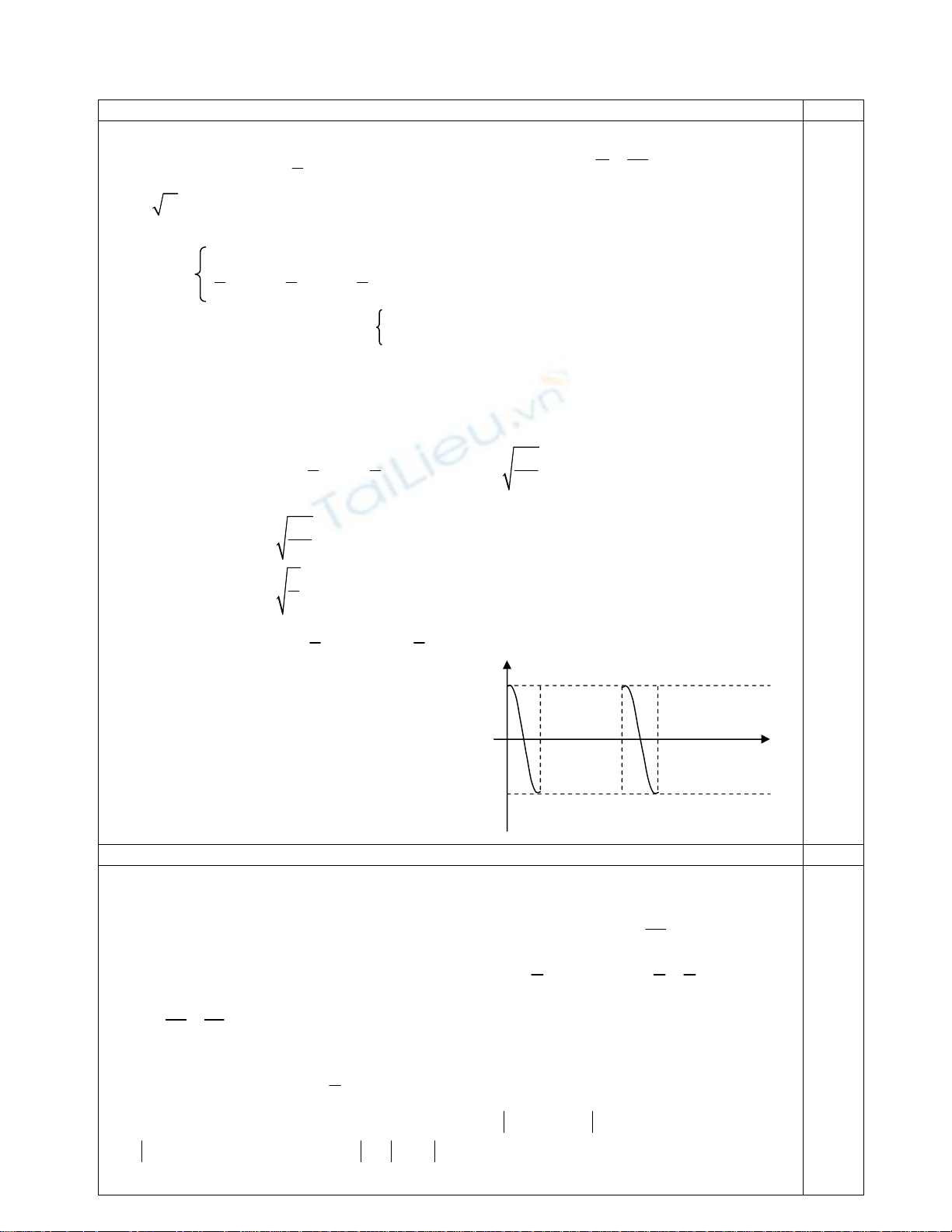
Bài 1
Con lắc đơn gồm quả cầu nhỏ khối lượng m1 = 100g và sợi dây lý
tưởng chiều dài là l = 1,0m. Con lắc lò xo gồm lò xo có khối lượng
không đáng kể, độ cứng k = 25
N
m
và quả cầu nhỏ khối lượng m2 = m1
(hình vẽ bên). Lấy g = 10
2
;
m
s
2 = 10. Bố trí hai con lắc sao cho khi hệ
cân bằng lò xo không biến dạng, sợi dây thẳng đứng. Kéo m
1
lệch khỏi
vị trí cân bằng để sợi dây lệch một góc nhỏ 0 = 0,1 rad rồi thả nhẹ.
a/ Tìm vận tốc của m2 ngay sau khi va chạm với m1 và độ nén cực đại của lò xo. Coi va chạm
là tuyệt đối đàn hồi (bỏ qua mọi ma sát).
b/ Tìm chu kì dao động của hệ.
c/ Vẽ đồ thị biểu diễn sự phụ thuộc của vận tốc theo thời gian của con lắc lò xo. Chọn gốc thời
gian là lúc va chạm.
Bài 2
Một sóng dừng trên một sợi dây mà phương trình sóng có dạng u = a.cos(ωt).sin(bx). Trong
đó u là li độ dao động tại thời điểm t của một phần tử trên dây mà vị trí cân bằng của nó cách gốc
toạ độ O một khoảng x (x đo bằng mét, t đo bằng giây). Cho λ = 0,4m, f = 50Hz và biên độ dao
động của một phần tử M cách một nút sóng 5cm có giá trị là AM = 5mm.
a/ Xác định a và b.
b/ Dây có hai đầu cố định và có chiều dài 2,2m. Hỏi có bao nhiêu điểm trên dây có biên độ
dao động 5mm.
Bài 3
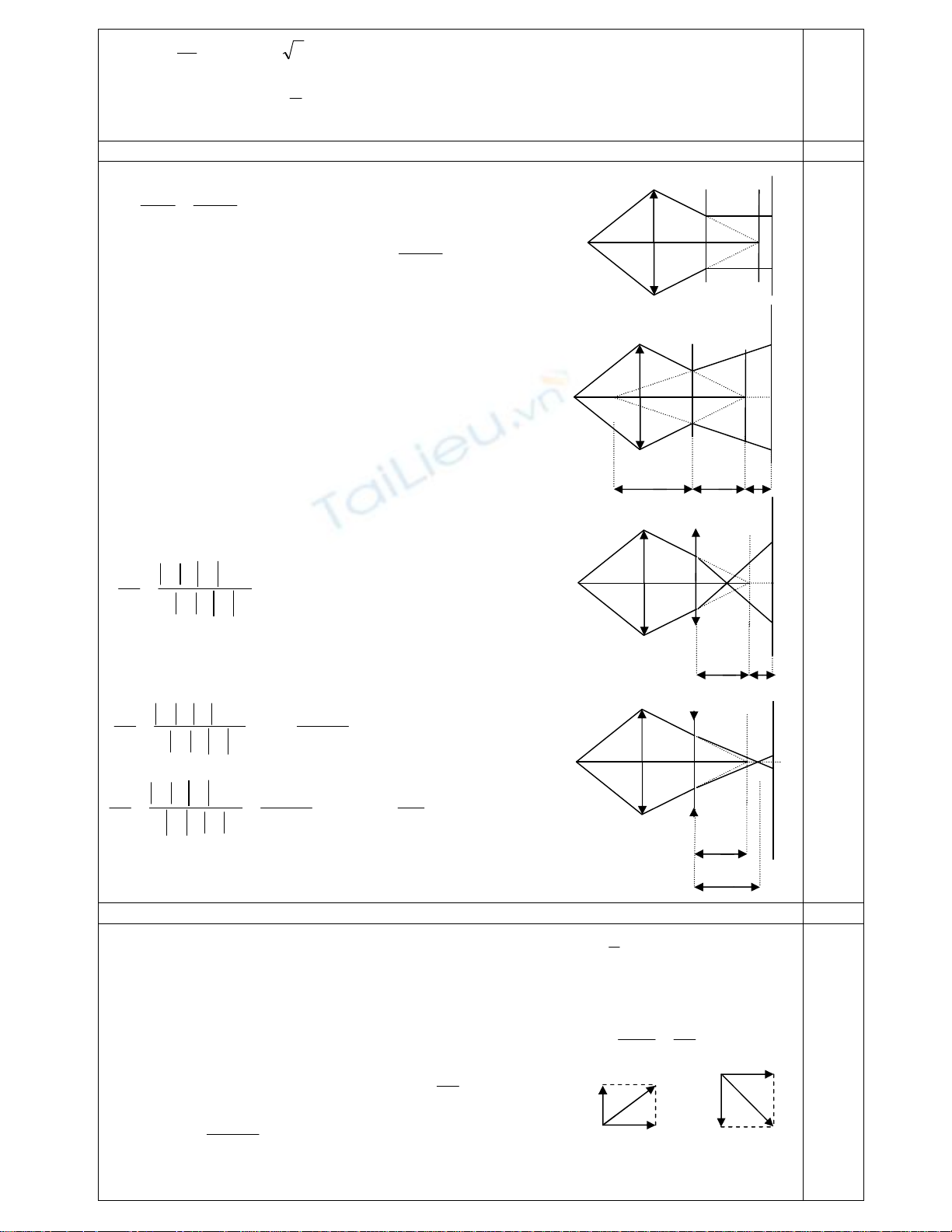
Một điểm sáng S đặt trên trục chính của một thấu kính hội tụ L1 có tiêu cự f1 = 25cm. Người ta
hứng được ảnh S’ của S trên màn E đặt vuông góc với trục chính.
1/ Xác định vị trí của vật, màn đối với thấu kính để khoảng cách giữa vật – màn nhỏ nhất.
2/ Vị trí vật, màn, thấu kính giữ nguyên. Đặt sau thấu kính L1 một thấu kính L2 đồng trục
với thấu kính L1 và cách thấu kính L1 một khoảng 20cm. Trên màn thu được một vết sáng. Hãy tính
tiêu cự của L2 trong các điều kiện sau:
a. Vết sáng trên màn có đường kính không đổi khi tịnh tiến màn.
b. Vết sáng trên màn có đường kính tăng gấp đôi khi tịnh tiến màn ra xa thêm 10cm.
Bài 4
Các hạt khối lượng m, mang điện tích q bay vào vùng không
gian giữa hai bản tụ điện phẳng dưới góc so với mặt bản và ra
khỏi dưới góc (hình bên). Tính động năng ban đầu của hạt, biết
điện trường có cường độ E, chiều dài các bản tụ là d. Bỏ qua hiệu
ứng bờ của tụ điện.
Bài 5
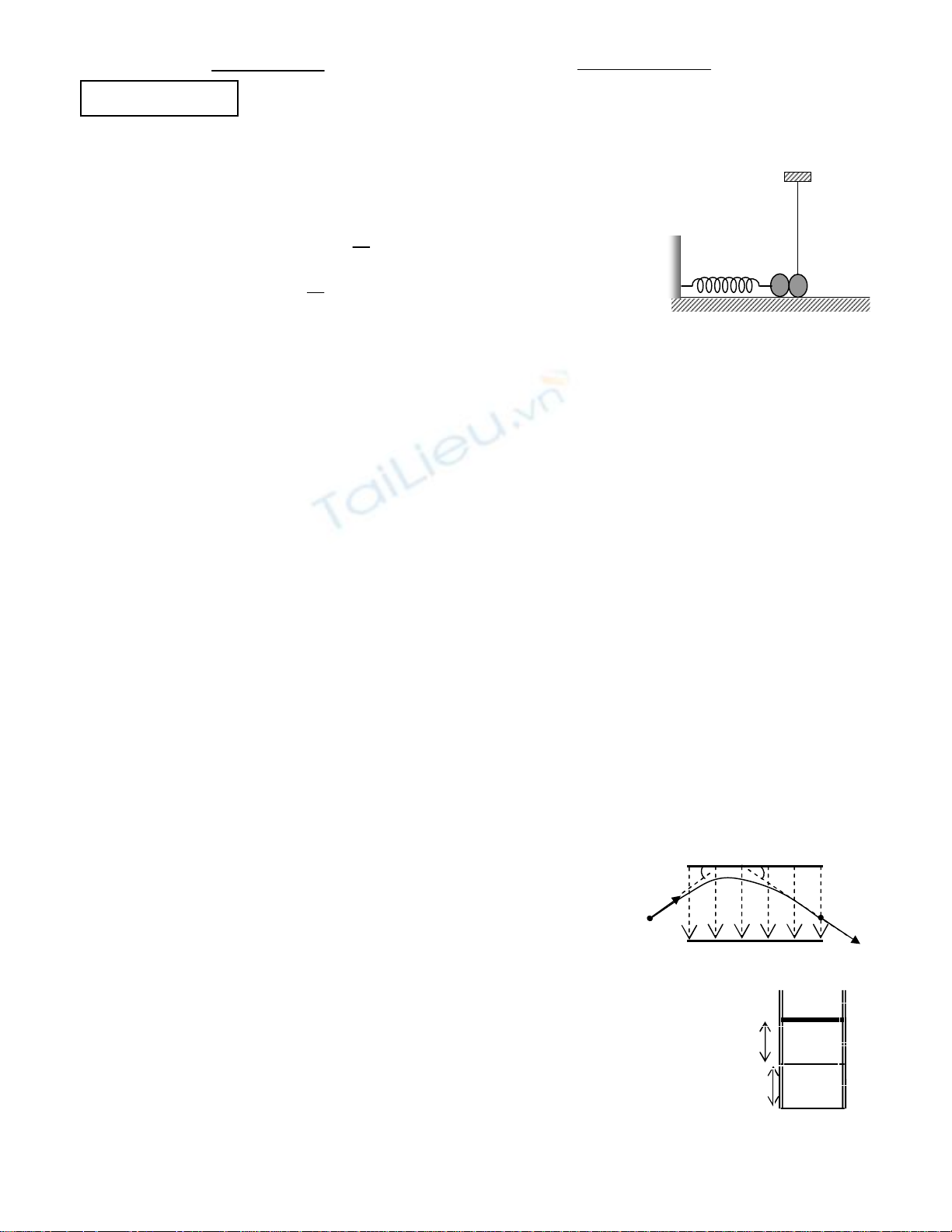
Trong một xy lanh thẳng đứng (thành và đáy cách nhiệt) có hai pit-tông: pit-
tông A dẫn nhiệt, pit-tông B cách nhiệt. Hai pit-tông và đáy xylanh tạo thành hai
ngăn, mỗi ngăn chứa 1 mol khí lí tưởng đơn nguyên tử và có chiều cao h = 0,5m.
Ban đầu hệ ở trạng thái cân bằng nhiệt. Làm cho khí nóng lên thật chậm bằng
cách cung cấp cho khí (qua đáy dưới) một nhiệt lượng Q = 100J. Pit-tông A có ma
sát với thành bình và không chuyển động, pit-tông B chuyển động không ma sát
với thành bình. Tính lực ma sát tác dụng lên pit-tông A.
=== Hết ===
Thí sinh không được sử dụng bất cứ tài liệu nào
ĐỀ CHÍNH THỨC
k
m
1
l
m
2
α ò
h
B
A
h
HƯỚNG DẪN CHẤM THI HSG VẬT LÍ 12 - Năm học 2011 - 2012
(gồm 03 trang)
Bài 1 (5,0đ) Điểm
a) Gọi vận tốc m1 ngay trước khi va chạm là v0:
m1gh = m1gl(1 - cos0) =
2
1 0
1
m v
2
=> góc 0 nhỏ 1 - cos = 2sin2
2
2 2
v0 =
gl
= 0,314 (m/s)
+ Gọi v1, v2 là vận tốc của m1, m2 ngay sau khi va chạm
m1v0 = m1.v1+ m2.v2 (1)
2
1 0
1
m v
2
=
2
1 1
1
m v
2
+
2
2 2
1
m v
2
(2)
vì m1 = m2 nên từ (1) (2) ta có v0= v1+ v2 (3)
2 2 2
0 1 2
v v v
(4)
Từ (3) suy ra:
2
0
v
= (v1+ v2)2 =
2
1
v
+
2
2
v
+ 2v1v2
So sánh với (4) suy ra: v1 = 0; v2 = v0 = 0,314 (m/s)
+ Như vậy, sau va chạm m1 đứng yên, m2 chuyển động với vận tốc bằng vận tốc của m1 trước khi
va chạm.
+ Độ nén cực đại của lò xo:
1
2
kl2=
1
2
m2v22 l = v2
2
m
k
= 0,02m = 2cm
b) Chu kì dao động
+ Con lắc lò xo: T1= 2 2
m
0,4s
k
+ Con lắc đơn: T2 = 2 l
2s
g
Chu kì dao động của hệ: T =
1
2
(T1 + T2) =
1
2
(2 + 0,4) = 1,2 (s)
c) Đồ thị
Tại t = 0 => v = v0
t = 0,1s => v = 0
t = 0,2s => v = -v0
t = 1,2s => v = v0
.
.
0,5
0,5
0,5
0,5
0,5
0,5
0,5
0,5
0,5
0,5
Bài 2 (5,0 đ)
a/* Xác định b:
- Phương trình sóng dừng trên dây: u = [a.sin(bx)].cos(ωt) = A.cos(ωt)
- Tại điểm nút thứ k có tọa độ xk: A = 0 => sin(bxk) = 0 k k
k
bx k x
b
Khoảng cách giữa hai nút liên tiếp của một sóng dừng bằng
2
nên xk+1 - xk=
b 2
.
Vậy b = 2
20
cm-1
* Xác định a:
- Tọa độ các điểm nút là xk =
k
b
= 20k(cm) với k = 0,
1, 2...
- Xét phần tử M cách nút thứ k 5cm có AM = 5mm => k
a sin b(x 5) 5mm
k k
a sin bx .cos5b cosbx .sin5b) a sin5b 5
0,5
0,5
0,5
0,5
0,5
0,5
0,5
t(s)
0
v
0
0,1 0,2 1,2 1,3
Thay b =
20
được a = 5 2 (mm)
b/ Chiều dài dây: l = max
k
2
=> kmax = 11 => có 11 bụng sóng, 12 nút sóng.
Giữa 2 nút có 2 điểm dđ với biên độ 5mm => Số điểm cần tìm 11.2 = 22 điểm.
0,5
0,5
0,5
Bài 3
(
4
,0 đ)
1/ Ảnh hứng được trên màn tức ảnh thật, ta có:
df 25d
d'
d f d 25
Khoảng cách từ ảnh đến vật: l = d + d’ = 2
d
d 25
d2 - l.d + 25.l = 0 => Δ = l2 - 100.l ≥ 0
=> lmin = 100cm;
d = 50cm.
2/ * Đặt thêm thấu kính L2 trên màn có vệt sáng không
đổi khi dịch chuyển màn chứng tỏ chùm tia ló sau
khi ra khỏi hệ thấu kính là chùm tia song song. (h.1)
Tức là d2 = f2. Mà d2 = O1O2 – d1’ = 20 – 50 = -30 cm.
Vậy L2 là thấu kính phân kỳ có tiêu cự f2 = -30cm.
* Khi đặt thêm thấu kính L2 dịch chuyển màn ra xa 10 cm
ảnh tăng gấp đôi. Xảy ra hai trường hợp:
Hoặc chùm tia ló là chùm tia hội tụ hoặc phân kì
TH1: Chùm tia ló phân kỳ(ảnh qua hệ là ảnh ảo) (h.2)
Qua hình vẽ ta thấy:
'
2 2 '
22
'
2 2
10
2 20
d d
Dd
Dd d
=> vô lý.
TH2: Chùm tia hội tụ (ảnh qua hệ là ảnh thật)
Xảy ra hai trường hợp:
a. L2 là thấu kính hội tụ: (h.3)
Qua hình vẽ ta thấy
'
2 1 '
2 2 2 2
'
'
1 2
2 2
10 40
2 2 20 60
30
d d
D d
d cm f cm
D d
d d
b. L2 thấu kính phân kỳ. (h.4)
''
2 2 '
2 2 2 2
'
'
1 2
2 2
10 40 100
2 300 .
30 3
d d
D d
d f cm
D d
d d
0,5
0,5
0,5
0,5
0,5
0,5
0,5
0,5
Bài 4
(
3
,0 đ)
Gọi v1 là vận tốc lúc hạt vào, thì động năng ban đầu của nó bằng:
2
1 1
1
W mv
2
(1)
Gọi v2 là vận tốc lúc hạt ra khỏi tụ điện, thì :
+ Thành phần vận tốc vuông góc với đường sức: v┴ =2 1
v cos v cos
= hs (2)
+ Thành phần vận tốc song song với đường sức thay đổi với gia tốc: F P Eq
a g
m m
=> v// =2 1 1 Eq
v sin v sin at v sin g t
m
(3)
Trong đó:
1
d
t
v cos
(4)
0,5
0,5
0,5
0,5
v
1
v
2
v
┴
v
//
v
//
v
┴
S O1 O2 S’
L1 L2 E1 E2
S O1 O2 S’
L1 L2 E1 E2
D2
D1
"
2
S
d2 10
S O1 O2 S’
L1 L2 E1 E2
D2
D1
''
2
S
d2' d2 10
h.1
h.
2
h.
3
h.
4
S
O1 O2 S’
L1 L2 E1 E2
D2
D1
''
2
S
d2
d2'
Thay v2 theo (2) và t theo (4) vào (3) được: 1 1
1
qE mg d
v cos .tg v sin .
m v cos
Suy ra: 2
2
1
(qE mg).d
cos .tg sin .cos mv
Do đó:
2
1 1 2
1 (qE mg)d
W mv
2 2cos tg tg
Nếu bỏ qua trọng lực:
2
1 1 2
1 q.E.d
W mv
2 2cos . tg tg
0,5
0,5
Bài 5 (3,0 đ)
Gọi nhiệt độ ban đầu của hệ là T0, nhiệt độ sau cùng của hệ là T1, p0 là áp suất ban đầu của hệ.
Xét ngăn trên: Khí thu nhiệt lượng Q1 tăng nhiệt độ đẳng áp từ T0 đến T1:
Q1 = Cp(T1 - T0) =
v 1 0 1 0 1 0
3 5
(C R)(T T ) ( R R)(T T ) R(T T )
2 2
Xét ngăn dưới: Khí thu nhiệt lượng Q2 nóng đẳng tích từ T0 đến T1:
Áp suất tăng từ p0 đến p1: 1
1 0
0
T
p p
T
2 2 v 1 0 2 1 0
3
Q U C .(T T ) Q R(T T )
2
Q = Q1 + Q2
1 0
Q 4R(T T )
Lực ma sát F tác dụng lên pit-tông A là:
1 0
F p p S
0 0 1 0
1 0
0
p V R(T T )
F T T
T h h
Q 100
F 50N.
4h 4.0,5
0,5
0,5
0,5
0,5
0,5
0,5
* Lưu ý:
- Học sinh giải đúng theo cách khác vẫn cho điểm tối đa.
- Điểm của mỗi ý trong câu có thể thay đổi nhưng phải được sự nhất trí của toàn bộ tổ chấm.
- Nếu thiếu từ 2 đơn vị trở lên, trừ 0,5 điểm cho toàn bài thi.
- Bài 4: Nếu HS bỏ qua trọng lực mà vẫn giải đúng chỉ trừ 0,5 đ cho toàn bài 4.
1
SỞ GD&ĐT THÁI NGUYÊN
KÌ THI CHỌN HỌC SINH GIỎI MTCT 12
Môn Vật Lí 2010 - 2011
ĐỀ + HƯỚNG DẪN CHẤM (Gồm 04 trang)
- Mỗi bài toán được chấm theo thang điểm 5.
- Phần cách giải: 2,5 điểm, kết quả chính xác tới 4 chữ số thập phân: 2,5 điểm.
- Nếu phần cách giải sai hoặc thiếu mà vẫn có kết quả đúng thì không có điểm.
- Nếu thí sinh làm đúng 1 phần vẫn cho điểm.
- Điểm của bài thi là tổng điểm của 10 bài toán.
Bài 1:
Một xe chuyển động thẳng nhanh dần đều đi được những đoạn đường s1=30m và s2=40m
trong khoảng thời gian liên tiếp bằng nhau là 3s. Tìm gia tốc và tốc độ ban đầu của xe ?
Đơn vị tính: Gia tốc(m/s2); tốc độ(m/s).
Cách giải Kết quả
Áp dụng công thức:
2
0
a.t
s v .t
2
Trong t1=3s có s1=35m
Trong t2=3s có s2=40m
ta có hệ phương trình: 3v0+4,5a = 30
3v
0
+13,5a = 40
Giải hệ
a=1,1111m/s2
v0=8,3333m/s
Bài 2:
Từ một điểm A cách mặt đất 20m người ta ném thẳng đứng lên trên một viên bi với tốc
độ ban đầu 10m/s. Bỏ qua sức cản của không khí. Lấy g = 9,8143m/s2.
a. Tính thời gian viên bi lên đến đỉnh cao nhất, viên bi trở lại A, viên bi rơi xuống đến
mặt đất?
b. Tính tốc độ của viên bi khi bắt đầu chạm mặt đất ?
Đơn vị tính: Thời gian(s); tốc độ(m/s).
Cách giải Kết quả
a. Chọn gốc O tại A, chiều dương lên trên
Phương trình toạ độ của viên bi :
2
0 0
g.t
y y v t
2
Vận tốc v=-gt+10
Khi lên vị trí cao nhất v = 0 => g
10
t1
Khi trở lại A: t2 = 2t1.
Khi đến mặt đất y = 0 => t3.
b. Thay vào công thức vận tốc, khi chạm đất t3 = 3,2805 s
a.
t1=1,0190s
thời gian lại A
t2 = 2,0380s
thời gian chạm đất
t3 = 3,2805s
b. v=-22,19289m/s