1
Sở Gd&Đt Nghệ an
ĐỀ THI CHỌN ĐỘI TUYỂN DỰ THI HSG QUỐC GIA LỚP 12
Năm học 2012-2013
Môn thi: VẬT LÝ (Đề thi có 2 trang)
Thời gian 180 phút (không kể thời gian giao đề)
Ngày thi: 07/11/2013
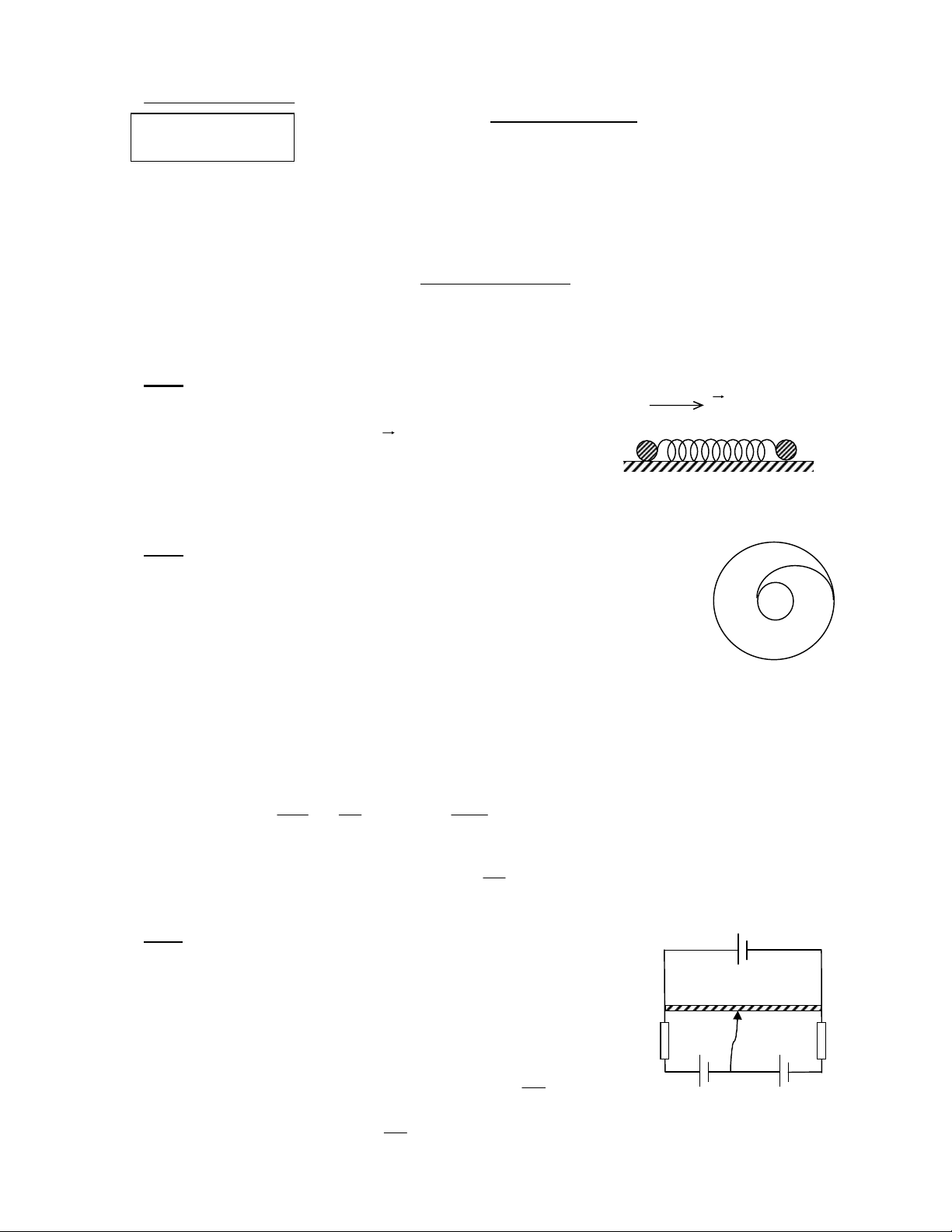
Bài 1 (4 điểm) Hai quả cầu nhỏ m1 và m2 được tích điện q và -q, chúng được nối với nhau bởi một
lò xo rất nhẹ có độ cứng K (hình 1). Hệ nằm yên trên mặt sàn nằm
ngang trơn nhẵn, lò xo không biến dạng. Người ta đặt đột ngột
một điện trường đều cường độ
E
, hướng theo phương ngang,
sang phải. Tìm vận tốc cực đại của các quả cầu trong chuyển
động sau đó. Bỏ qua tương tác điện giữa hai quả cầu, lò xo và mặt
sàn đều cách điện.
Bài 2 (4 điểm) Một vệ tinh chuyển động tròn đều quanh Trái Đất ở độ cao
R = 3R0 so với tâm O của Trái Đất (Bán kính Trái Đất là R0 = 6400 km).
1. Tính vận tốc V0 và chu kỳ T0 của vệ tinh.
2. Giả sử vệ tinh bị nhiễu loạn nhẹ và tức thời theo phương bán kính sao
cho nó bị lệch khỏi quỹ đạo tròn bán kính R trên. Hãy tính chu kỳ dao động
nhỏ của vệ tinh theo phương bán kính và xung quanh quỹ đạo cũ.
3. Vệ tinh đang chuyển động tròn bán kính R thì tại điểm A vận tốc đột ngột
giảm xuống thành VA nhưng giữ nguyên hướng, vệ tinh chuyển sang quỹ
đạo elip và tiếp đất tại điểm B trên đường OA (O, A, B thẳng hàng). Tìm
vận tốc vệ tinh tại A, B và thời gian để nó chuyển động từ A đến B.
Cho vận tốc vũ trụ cấp 1 là V1 = 7,9 km/s. Bỏ qua lực cản.
Có thể dùng phương trình chuyển động của một vệ tinh trên quỹ đạo:
2
2
2
2
r
Mm
Gr
dt
d
dt
rd
m
và định luật bảo toàn mômen động lượng: const
dt
d
mr2
.
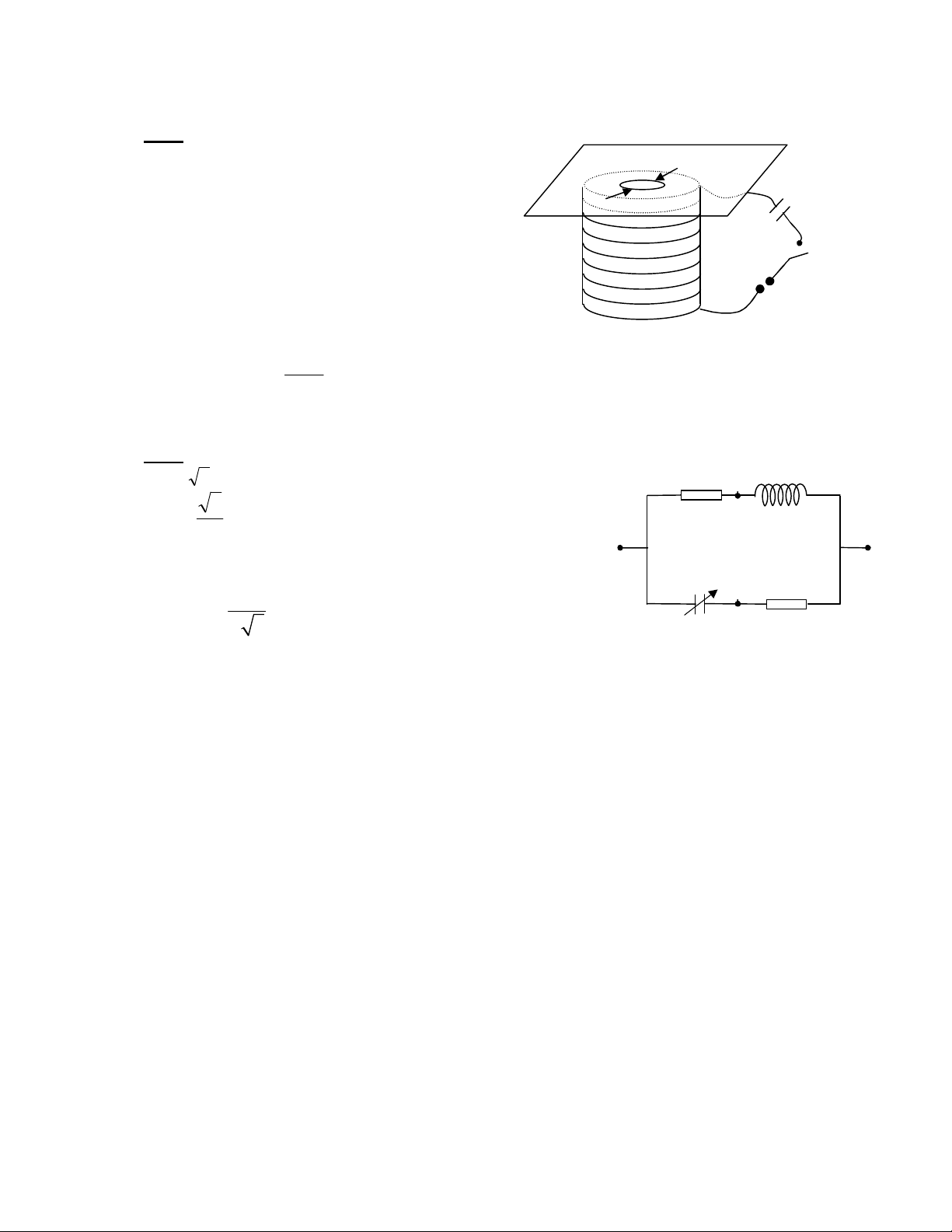
Bài 3 (4 điểm) Cho mạch điện như hình vẽ 3, biết E1= e, E2 = 2e, E3
= 4e, R1 = R, R2 = 2R, AB là dây dẫn đồng chất, tiết diện đều có
điện trở toàn phần là R3 = 3R. Bỏ qua điện trở trong của các nguồn
điện và dây nối.
1. Khảo sát tổng công suất trên R1 và R2 khi di chuyển con chạy C
từ A đến B.
2. Giữ nguyên vị trí con chạy C ở một vị trí nào đó trên biến trở.
Nối A và D bởi một ampe kế (RA 0) thì nó chỉ I1 =
R
E4, nối ampe
kế đó vào A và M thì nó chỉ I2=R
E
2
3. Hỏi khi tháo ampe kế ra thì
E
(Hình 1)
m
1
,q K m
2
,
-
q
.
B
O
A
(Hình 2)
ĐỀ CHÍNH THỨC
E3
A B
R2
C
R1
E
1 E2
(H×nh 3)
D
M
N
+
-
+
-
+
-
2
cường độ dòng điện qua R1 bằng bao nhiêu?
Bài 4 (4 điểm) Phía trên của một hình trụ solenoit đặt thẳng đứng có một tấm bìa cứng nằm ngang
trên đó đặt một vòng tròn nhỏ siêu dẫn làm từ dây
kim loại có đường kính tiết diện dây là d1, đường
kính vòng là D (d1 << D). Nối solenoit với nguồn
và tụ điện (hình 4), đóng khóa K thì vòng sẽ nẩy
lên khi hiệu điện thế U U0 (U0 là hiệu điện thế
xác định). Thay vòng trên bằng vòng siêu dẫn khác
cùng kim loại trên và cùng đường kính D còn
đường kính tiết diện dây là d2. Hỏi hiệu điện thế
nguồn điện là bao nhiêu để khi đóng khóa K thì
vòng vừa được thay nẩy lên. Biết độ tự cảm của
vòng là L = kD.ln
d
D4,1 (k là hằng số). Điện trở
thuần của solenoit và dây nối được bỏ qua.
Bài 5 (4 điểm) Cho mạch điện xoay chiều như hình vẽ. Biết uAB
= 180 2sin(100t) (V), R1 = R2 = 100 , cuộn dây thuần cảm
có L = H
3
, tụ điện có điện dung C biến đổi được.
1. Tìm C để hiệu điện thế hiệu dụng giữa hai điểm M, N đạt cực
tiểu.
2. Khi C = 100
F
3
, mắc vào M và N một ampe kế có điện trở
không đáng kể thì số chỉ ampe kế là bao nhiêu?
Hết
Họ tên thí sinh: …………………………………………SBD: ………...........
(Hình 4)
+
_
K
U
C
D
B
R1 M
L
A C N
R
2
(H×nh 5)
3
Sở Gd&Đt Nghệ an
----------------------
KỲ THI CHỌN ĐỘI TUYỂN DỰ THI HSG QUỐC GIA LỚP 12
Năm học 2012-2013
hướng dẫn chấm, đáp án và biểu điểm chấm đề chính thức
Môn: VẬT LÝ
Ngày thi: 07/11/2013
-~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
N
ộ
i dung
Đ
i
ể
m
Bài1 .Do tổng ngoại lực tác dụng hệ kín theo phương ngang
nên khối tâm của hệ đứng yên và tổng động lượng của hệ
được bảo toàn. Chọn trục Ox có phương ngang hướng
sang phải, góc O ở khối tâm của hệ. Ta có:
m1v1 + m2v2 = o
v2 = -
2
11
m
vm (1)
1đ
.Vật m1 và m2 sẽ dao động điều hòa xung quanh vị trí cân bằng của chúng, tại đó hợp lực
tác dụng lên mỗi vật bằng 0 và vận tốc của chúng đạt cực đại. Ta có:
1đ
qE = k(x1-x2) (2)
2
2
11vm +
2
2
22vm +
2
)( 2
21 xxk = qE(x1-x2) (3)
1đ
.Từ (1) và (2) và (3) ta được:
V1=)( 211
2
mmm
m
k
qE
, V2=)( 212
1
mmm
m
k
qE
1đ
Bài 2 1.Gọi M và m lần lượt là khối lượng Trái Đất và vệ tinh.
.Lực hấp dẫn của Trái Đất lên vệ tinh đóng vai trò lực hướng tâm nên:
R
mv
R
GMm 2
0
2
V0=
0
3R
GM =3
1
V=4,56m/s
0,5đ
.Chu kỳ quay của vệ tinh: T0 =
0
2
V
R
=26442s = 7,43h 0,5đ
2.Từ hai phương trình cho ở đề bài ta được phương trình:
2
2
dt
rd -3
2
)/(
r
mc = - 2
r
GM (1)
0,5đ
.Khi vệ tinh chuyển động với bán kính R thì: 2
)(m
c= GMR (2)
.Từ (1) và (2), ta được: 2
2
dt
rd -3
r
GMR =2
r
GM với r =R+x .
.Hay:
2
2
dt
xd
33 )1(
R
x
R
GMR
=
22 )1(
R
x
R
GM
0,5đ
.Do vệ tinh chỉ dao động bé nên x << R nên ta được phương trình dao động của vệ tinh:
x’’+x
R
GM
2= 0
.Chu kỳ dao động của vệ tinh là : T= GM
R2
0
9
2
=
1
1
6V
=21,2.10-2s
0,5đ
3.Áp dụng định luật bảo toàn mô men động lượng và bảo toàn cơ năng ta có: 0,5đ
E
o
m1,q K m2, - q
.
x
4
VA.3R = VB.R (1)
2
2
A
vm -
0
3R
GMm =
2
2
B
vm -
0
R
GMm (2)
.Từ (1) và (2) ta được: vA= v1/6= 3,23m/s , vB = 9,68m/s 0,5đ
.Bán kính trục lớn quĩ đạo elíp của vệ tinh: a = AB/2 = 2R0
.Áp dụng định luật 3 kêple ta có:
3
2
0
2
3
T
R
T
a
T=T0a
R0
a
R = 4h
.Thời gian vệ tinh chuyển động từ A đến B là: t = T/2 = 2h
0,5đ
Bài 3 1.Đặt RAC= x. Công suất tỏa nhiệt trên R1 và R2:
P =
1
2
R
UAM +
2
2
R
UNB
(1)
.Trong đó : UAM = UAC- e (2)
.U BN = - 4e + UAM+ e + 2e
UBN = UAC- 2e (3)
M N
0,5đ
.Thay (1), (2) vào (3) ta được: P =
2
R
eU AC +
2
2
2
R
eU AC 0,5đ
.Lấy đạo hàm hai vế của P theo UAC ta được : P’= 0
UAC= 3
4e
.Lập bảng biến thiên biểu diễn sự phụ thuộc của P theo UAC ta thấy UAC đạt cực tiể
u khi
UAC=3
4e, lúc đó Pmin=R
e
3
2
.
0,5đ
.Thay UAC vào (2) và (3) ta được: UAC =
3
evà UNB = 3
2e
.Từ đó tìm được: I1=
1
R
UAM
R
e
3 I2=
R
UNB
2R
e
3
ICD= 0
I3=
3
R
UAB
R
e
3
4
x = R
I
UAC
3
0,5đ
.Biện luận: -Khi x= 0 thì UAC= 0 và P =
R
e2
3.
-Khi x = R thì UAC=3
4e và Pmin =
R
e
3
2
.
-Khi x = 3R thì UAC=4e và Pmax =
R
e2
11 .
0,5đ
2.Coi phần mạch điện giữa A và D tương ứng với nguồn điện có suất điện động E và điện
trở trong r, mạch được vẽ lại như hình bên.
.Khi nối Ampe kế vào A và D thì:
I1=
R
e4 =
R
e+
r
e
r
E =
R
e3 (1)
.Nối Ampe kế vào A và M thì R1 bị nối tắt:
I2 =
R
e
2
3 =
r
eE
(2)
1đ
E,r
A
R1
M
E
1
D
E
3
A
R
2
C
R
1
E
1
E
2
I
3
I
1
I
2
D
5
.Giải hệ (1) và (2) ta được: E = 2e , r =
3
2R
.Khi không có Ampe kế thì cường độ dòng điện qua R1 là:
IR1 = rR
eE
1
=
R
e
5
3 = 0,6
R
e (A)
0,5đ
Bài 4 . Sau khi đóng khóa, gọi cường độ trong mạch là i và điện tích của tụ điện là q.
.Định luật ôm cho mạch: U – Ldi’=
q. Hay q’’+
d
cL
cUq
= 0 (1)
.Đặt q1 = q-cU, ta được phương trình: q1’’+2
q1 = 0.
.Nghiệm của phương trình là: q1 = Asin(
t
) + Bcos(
t
) (2)
0,5đ
.Chọn t = 0 là thời điểm đóng khóa K, ta có:
q1(t= 0) = q(t=o)– cU = cU, q1’= q’= 0
.Suy ra : A = 0 , B = - cU, q = cU[1- cos(
t
)] (3)
0,5đ
.Cường độ trong cuộn dây là: id = q
’
= cU
Sin(
t
)
id ~ U
.Đối với vòng siêu dẫn: ,
= -Lvi,v (4)
.Ở đây
là từ thông do cảm ứng từ xolenoit gửi qua vòng, iv là cường độ dòng điện
chạy qua vòng, LV là độ tự cảm của vòng.
.Nghiệm của (4) có dạng:
+ Lviv = C với C là hằng số.
.Tại thời điểm ban đầu C = 0 nên: iv = -
V
L
0,5đ
0,5đ
.Từ thông
tỷ lệ với độ tự cảm của solenoit (độ tự cảm này tỷ lệ id) và diện tích vòng:
~ idD2 ~ UD2
i v ~
v
L
UD2
0,5đ
.Lực Ampe cực đại tác dụng lên vòng theo hướng thẳng đứng lên trên, tỷ lệ với đường
kính của vòng, cường độ dòng điện trong vòng và trong solenoit.
F ~ Didiv ~
v
L
UD 23
0,5đ
.Vòng sẽ nảy lên nếu lực F lớn hơn trọng lực của vòng, trọng lực này tỷ lệ với Dd
2
.
.Trong trường hợp giới hạn:
v
L
UD 23
~ Dd2
U ~ V
LD
d
0,5đ
.Trường hợp đầu : U0 ~ d1{Ln(1,4D/d1)} 2/1
.Trường hợp sau : U’0 ~ d2{Ln(1,4D/d2)} 2/1
.Vòng sẽ nảy lên khi hiệu điện thế của nguồn thỏa mãn:
U’0
U0 d2{Ln(1,4D/d2)} 2/1 / d1{Ln(1,4D/d1)} 2/1
0,5đ
Bài 5 1.Giản đồ véc tơ được vẽ như hình bên.
.Từ giản đồ suy ra UMN cực tiểu khi M trùng với N .
.Hay: UMN= 0
UR1 = UC
I1R1 = I2ZC , UR2 = UL
= I2R2= I1ZL
1đ
L
Z
R
1 =
2
R
ZC
ZC =
L
Z
RR 21 =
3
100
C = F
3100 = 55( F
) 0,5đ
UR1 UR2
C
U UL
N M
U
AB
A
B