
S GD&ĐT ĐI NỞ Ệ
BIÊN
Đ thi chính th cề ứ
K THI CH N H C SINH GI I Ỳ Ọ Ọ Ỏ
L P 12 THPT C P C S - NĂM H C 2009 -2010Ớ Ấ Ơ Ở Ọ
Môn:Toán
Th i gian làm bài 180 phút, không k th i gian giaoờ ể ờ
đề
Ngày thi: 07/01/2010
(Đ thi có 01 trang)ề
Đ BÀIỀ
Câu 1: (6 đi m)ể
1. Cho ph ng trình: (1) (ươ m là tham s ).ố
a) Gi i ph ng trình (1) v i ả ươ ớ m = 0.
b) Tìm m đ ph ng trình (1) có nghi m.ể ươ ệ
2. Gi i h ph ng trình: ả ệ ươ
Câu 2: (5 đi m)ể
1. Tìm GTLN c a hàm s : trên đo n .ủ ố ạ
2. Cho hàm s có đ th là (C). Tính di n tích tam giác có các đnh là các đi m c cố ồ ị ệ ỉ ể ự
tr c a đ th (C).ị ủ ồ ị
Câu 3: (6 đi m)ể
1. Trong m t ph ng t a đ Oxy. Ch ng minh r ng v i m i giá tr c a ặ ẳ ọ ộ ứ ằ ớ ọ ị ủ t đngườ
th ng (d) có ph ng trình: (ẳ ươ t là tham s ) luôn ti p xúc v i m t đng tròn c đnh.ố ế ớ ộ ườ ố ị
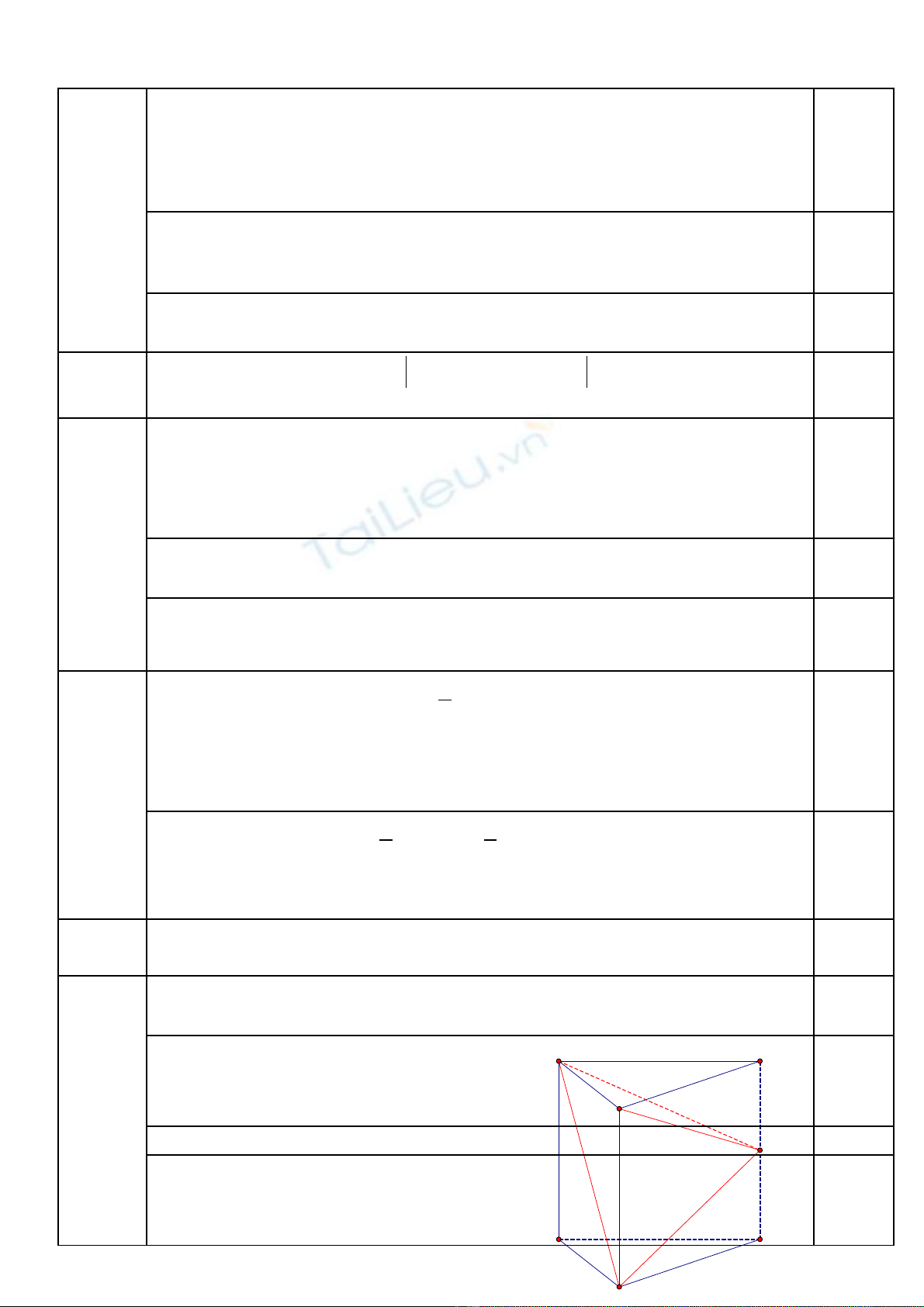
2. Cho lăng tr đng ABC.Aụ ứ 1B1C1 có AB = a, AC = 2a, AA1 = và . G i M là trung ọ
đi m c a CCể ủ 1. Ch ng minh MB MAứ1 và tính kho ng cách t A đn m t ph ng ả ừ ế ặ ẳ
(A1BM).
Câu 4: (1.5 đi m) ể
Cho đa th c có các h s không âm và có n nghi m th c. Ch ng minh . ứ ệ ố ệ ự ứ
Câu 5: (1.5 đi m)ể
1 2sin 1 sin
2 3.2 4
x x m
+ +
− = −
6 6
5 5
1
1
x y
x y
+ =
+ =
3 2
3 72 90y x x x= − + + −
[ ]
7;7−
4 2
12 3
4
y x x= − +
cos sin sin 2cos 3 0x t y t t t+ + − − =
2 5a
ᄋ
120BAC =
o
⊥
( )
1 2
1 2 1
1
n n n
n n
f x x a x a x a x
− −
− −
= + + + + +L
( )
2 3
n
f

Cho hàm s : có đ th là (C). là đi m trên (C) có hoành đ . Ti p tuy n c a (C)ố ồ ị ể ộ ế ế ủ
t i c t (C) t i đi m khác , ti p tuy n c a (C) t i c t (C) t i đi m khác , ti p tuy nạ ắ ạ ể ế ế ủ ạ ắ ạ ể ế ế
c a (C) t i đi m c t (C) t i đi m khác (n = 4; 5;…), g i là t a đ đi m . ủ ạ ể ắ ạ ể ọ ọ ộ ể
Tìm n đ : ể
----------H t----------ế
ĐÁP ÁN Đ THI CHÍNH TH C H C SINH GI I MÔN TOÁN 12Ề Ứ Ọ Ỏ
NĂM H C 2009-2010Ọ
Câu 1 N I DUNGỘ6đi mể
1
(4đi mể
)
Đt ta có ph ng trình: (2)ặ ươ
0.5
a.V i m = 0 suy ra:ớ0.5
1
b.ycbt(2) có nghi m ệ
0.5
(2) có nghi m khi đng th ng y = m c t trên ệ ườ ẳ ắ
0.5
…… 0.5
Suy ra thì (1) có nghi mệ
0.5
3
2009y x x= −
1
M
1
1x=
1
M
2
M
1
M
2
M
3
M
2
M
1n
M
−
n
M
1n
M
−
( )
;
n n
x y
n
M
2013
2009 2 0
n n
x y+ + =
1 2sin 1 sinx
2 3.2 4
x
m
+ +
− = −
sinx
1
2 ;2
2
t t � �
=�� � �
� �
2
2 6 4t t m− = −
2
2 6 4 0 1 2t t t t− + = = =� �
sinx
1 2 1 sinx 0t x k
π
= = = =� � �
sinx
2 2 2 sinx 1 2
2
t x k
ππ
= = = = +� � �
1;2
2
t� �
� �
� �
( )
2
2 2 6 4t t m− + =�
( )
2
: 2 6 4P y t t= − +
1;2
2
� �
� �
� �
( )
1 3 3 1
; ; 2 0
2 2 2 2
y y y
� � � �
= = − =
� � � �
� � � �
1 3
2 2
m−
M
B'
C'
B
C
A
A'
2
(2đi mể
)
L p lu n t (1) và (2) suy ra và x, y không cùng d uậ ậ ừ ấ
0.75
Vai trò c a x, y bình đng , không làm m t tính t ng quát gi s ủ ẳ ấ ổ ả ử
. L p lu n đa ra h vô nghi mậ ậ ư ệ ệ
0.75
Nh n th y là các nghi m c a hậ ấ ệ ủ ệ
0.5
Câu 2
trên đo n ạ
4
đi mể
1
(2đi mể
)Xét hàm trên
0.5
1.0
0.5
2
(2đi mể
)
Các đi m c c tr : ể ự ị
1.0
NX: các đi m c c tr t o thành tam giác cân t i C. Suy ra di n tích đcể ự ị ạ ạ ệ ượ
tính:
1.0
Câu 3 6
đi mể
1
(2đi mể
)(*)
0.5
tìm các đi m mà đng th ng không đi qua v i m i t hay (*) vô ể ườ ẳ ớ ọ
nghi m xét đt (C )ệ
0.5
C/M đng tròn ( C ) ti p xúc (d) v i m i tườ ế ớ ọ 0.5
V y đng th ng đã cho luôn ti p xúc v i đng tròn c đnh có ậ ườ ẳ ế ớ ườ ố ị
ph ng trình : ươ
0.5
6 6
5 5
1 (1)
1 (2)
x y
x y
+ =
+ =
[ ]
, 1;1x y −�
1 0 1x y− < < < <
( ) ( )
0;1 ; 1;0
3 2
3 72 90y x x x= − + + −
[ ]
7;7−
( )
3 2
3 72 90f x x x x= − + + −
[ ]
7;7−
2
' 3 6 72 0 4 6y x x x x= − + + = = − =� �
( ) ( ) ( ) ( )
4 266; 6 234; 7 218; 7 104y y y y− = − = = − = −
[ ]
( )
7;7
max 4 266y y
−
= − =
4 2
12 3
4
y x x= − +
( ) ( ) ( )
2; 1 ; 0;3 ; 2; 1A B C− − −
( )
1 1
. 4.4 8
2 2
S BH AC dvdt= = =
( ) ( )
cos sin sin 2cos 3 0 1 sin 2 cos 3x t y t t t y t x t+ + − − = + + − =�
( ) ( )
2 2 2
1 2 3y x+ + − <�
( ) ( )
2 2 2
1 2 3y x+ + − =
( ) ( )
2 2 2
1 2 3y x+ + − =

2
(4đi mể
)
a. Ch ng minh .ứ
0.75
0.75
Suy ra 0.5
b.Tính kho nh cách t A đn mp(A’BM)ả ừ ế
0.5
0.5
0.5
0.5
'MB MA⊥
uuur uuuur
( )
1
' ' ' ' AA'
2
A M A C C M AC
� �
= + = −
� �
� �
uuuuur uuuur uuuuur uuur uuuur
1 1
. ' AA' AA'
2 2
BM A M AB AC AC
� �� �
= − + + −
� �� �
� �� �
uuuur uuuuur uuur uuur uuuur uuur uuuur
( ) ( )
1AA'
2
BM BA AM AB AC CM AB AC
� �
= + = − + + = − + +
� �
� �
uuuur uuur uuuur uuur uuur uuuur uuur uuur uuuur
( )
2 2
2
2 2
1 1 1 1
. .AA' .AA' AA'. AA'
2 2 2 4
1
4 2 5 0
4
AB AC AB AC AC AC
a a a
� �
= − + + − + −
� �
� �
= + − =
uuur uuur uuur uuuur uuur uuuur uuuur uuur
'MB MA⊥
uuur uuuur

Câu 5
2 đi mể
G i suy ra ti p tuy n t i ọ ế ế ạ
0.5
T a đ đi m đc xác đnh: ọ ộ ể ượ ị
0.5
Ta có :
0.5
0.5
Câu 4
2 đi mể có các h s không âm và n nghi m th c . Suy n nghi m đó âm gi s ệ ố ệ ự ệ ả ử
là các nghi m:ệ
0.5
Theo cách phân tích đa th c ta đc ứ ượ
0.5
( )
( )
( )
( )
( )
( )
( )
( )
. ' ' AA'
'
2 2 2 2 2 0 2 2
2 2 2 2
2
'
2 0
AA'
1 1
, ' . , AA' .
3 3
1. '
2
1
2. . .cos120 AA' 12
4
' ' ' ' 9
13 . 12 3 3
2
1 3
2 .2 5 2 5; , AA' .sin60
2 2
, '
A A BM A BM M
A BM
A BM
M
V d A A BM S d B M S
S MB MA
MB BC CM AB AC AC AB a
MA A C C M a
S a a a
a
S a a a d B M BH AB
d A A BM
= =
=
= + = + − + =
= + =
= =�
= = = = =
( )
( )
2 2
3 5
.3 3 2 5. , '
2 3
a
a a d A A BM a= =�
3
2009y x x= −
( )
;
k k k
M x y
( ) ( )
: '
k k k k
M y y y x x x− = −
( )
( )
2 3
3 2009 2009
k k k k
y x x x x x= − − + −�
1k
M
+
( )
( )
( )
( )
3 2 3
2 2
1
2009 3 2009 2009
. 2 0 2
2
k k k k
k k k k k
k k
x x x x x x x
x x x x x x x x x x
x x
+
− = − − + −
− + − = = = −� � �
= −�
( )
1
1 2 3
1; 2; 4;...; 2
n
n
x x x x
−
= = − = = −
( ) ( )
2010 3 2010
3 3 2013
2013
2009 2 0 2009 2009 2 0
2 2 2 3 3 2013 672
n n n n n
n
x y x x x
n n
−
+ + = + − + =�
− = − = − − = =� � �
( )
1 2
1 2 1
1
n n n
n n
f x x a x a x a x
− −
− −
= + + + + +L
, 1,2,...,
i
x i n=
( )
( )
1
n
i
i
f x x x
=
= Π −












![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)



