PHÒNG GIÁO D C VÀ ĐÀOỤ
T OẠ
L C NG NỤ Ạ
Đ THI CHÍNH TH CỀ Ứ
(Đ thi g m có 01 trang)ề ồ
K THI CH N H C SINH GI I C P HUY N Ỳ Ọ Ọ Ỏ Ấ Ệ
NĂM H C 2014-2015Ọ
Môn: Toán l p 6ớ
Th i gian làm bài: 120 phútờ
Câu 1 (4 đi m)ể. Th c hi n phép tínhự ệ :
1)
7 7 5 21 49 8
. . .
13 15 12 39 91 15
− +
2)
12 23 34 1 1 1
.
199 200 201 2 3 6
� �� �
+ − − −
� �� �
� �� �
Câu 2 (6 đi m)ể
1) Tìm các ch s a, b bi t: ữ ố ế
75 3 45a bM
2) S sách ngăn A b ng ố ở ằ
3
2
s sách ngăn B. N u chuy n 22 quy n t ngăn Aố ở ế ể ể ừ
sang ngăn B thì s sách ngăn A b ng ố ở ằ
7
1
s sách ngăn B. Tìm s sách m i ngăn.ố ở ố ở ỗ
3) Tìm s t nhiên x bi t: ố ự ế
2 1
2 32
x
−
=
Câu 3 (3 đi m). Cho ể
7
5
An
−
=−
1) Tìm các s nguyên n đ A là phân s .ố ể ố
2) Tìm các s nguyên n sao cho A có giá tr là s nguyên.ố ị ố
Câu 4 (6 đi m)ể
Cho
ﾷ
xAy
khác góc b t, trên tia Ax l y đi m B sao cho AB = 6 cm. Trên tia đi c a ẹ ấ ể ố ủ
tia Ax l y đi m D sao cho AD = 4 cm.ấ ể
1) Tính BD.
2) L y C là m t đi m trên tia Ay. ấ ộ ể Bi t ế
ﾷ
BCD
= 800,
= 450. Tính
ﾷ
ACD
.
3) Bi t AK = 2 cm (K thu c BD). Tính BK ? ế ộ
Câu 5 (1 đi m)ể
Tìm s các s nguyên t x và y sao cho các s 5x + y và xy + 13 cũng là các số ố ố ố ố
nguyên t .ố
.................................... H t ......................................ế
H và tên: ........................................................ S báo danh: ......................ọ ố
PHÒNG GD&ĐT L C NG NỤ Ạ ĐÁP ÁN - THANG ĐI MỂ
MÔN: TOÁN L P 6Ớ
(Đáp án - thang đi m g m 03 trang)ể ồ
H ng dân châm nay chi trinh bay s l c môt cach giai. Bai lam cua hoc sinh phai chi ươ ơ ươ
tiêt, lâp luân chăt che, tinh toan chinh xac m i đc cho điêm tôi đa. Trong cac phân co ơ ươ
liên quan đên nhau, nêu hoc sinh lam sai phân tr c thi phân sau liên quan đên no du ươ
đung cung không đc tinh điêm. Tr ng h p sai sot nho co thê cho điêm nh ng tr ươ ươ ơ ư ư
điêm chô sai đo. Không cho điêm bai hinh nêu hoc sinh không ve hinh.
CâuÝN i DungộĐiể
m
Câu
1
1
13
7
.
15
7
-
12
5
.
39
21
+
91
49
.
15
8
=
13
7
.
15
7
-
12
5
.
13
7
+
13
7
.
15
8
0.5
=
13
7
(
15
7
-
12
5
+
15
8
)0.5
=
13
7
(1-
12
5
)0.5
=
13
7
12
7
=
156
49
0.5
2 (
199
12
+
200
23
-
201
34
)
(
2
1
-
3
1
-
6
1
)
= (
199
12
+
200
23
-
201
34
)
(
6
3
-
6
2
-
6
1
)
1
= (
199
12
+
200
23
-
201
34
)
0 = 0 1
Câu
2
1
Ta có đ: ể
75 3 45a bM
Thì
75 3 5 (1)
75 3 9 (2)
a b
a b
M
M
T (1) => b= 0 ho c b = 5ừ ặ
* Khi b = 5 ta có:
75 3a b
=
75 30a
L i do (2) => 7 + 5 + a + 3 ạ
M
9
hay 15 + a
M
9 => a = 3. Ta có: a = 3; b = 0.
* Khi b = 5 ta có:
75 3a b
=
75 35a
L i do (2) => 7 + 5 + a + 3+5 ạ
M
9
hay 20 + a
M
9 => a = 7. Ta có: a = 7; b = 5.
K t lu n:.....................ế ậ
0.25
0.5
0.5
0,5
0,25
2Lúc đu s sách ngăn A b ng ầ ố ở ằ
5
2
23
2
t ng s sách c 2 ngănổ ố ở ả 0.25
N u chuy n 22 quy n sách t ngăn A sang ngăn B thì s sách ngăn Aế ể ể ừ ố ở
b ng ằ
8
1
17
1
t ng s sách 2 ngănổ ố ở
0.25
Suy ra 22 quy n ng v i ể ứ ớ
40
11
8
1
5
2
t ng s sách 2 ngănổ ố ở 0.5
T ng s sách 2 ngăn là: 22:ổ ố ở
40
11
= 80 (quy n)ể
S sách ngăn A là: 80.ố ở
32
5
2
(quy n)ể
0.25
0.25
S sách ngăn B là: 80 - 32 = 48 (quy n)ố ở ể 0.25
Đáp s : Ngăn A: 32 quy nố ể
Ngăn B: 48 quy nể
0.25
3Tacó:
2 1
2 32
x
−
=
2 1 5
2 2
2 - 1 = 5
<=> 2x = 6
<=> x = 3
x
x
−
<=> =
<=>
0.5
0,5
0,5
0,5
Câu
3
1Để
7
5
An
−
=−
là phân s thì ta ph i có: ố ả
5 0 <=> n 5n
−
1
2Đ ể
7
5
An
−
=−
có giá tr là s nguyên thì: - 7 chia h t cho n - 5ị ố ế
Hay n - 5
( 7)U−�
0,5
05
=> n - 5
{ }
7; 1 ; 1; 7− −
=> n
{ }
2; 4 ; 6; 12−
0,75
KL:............... 0,25
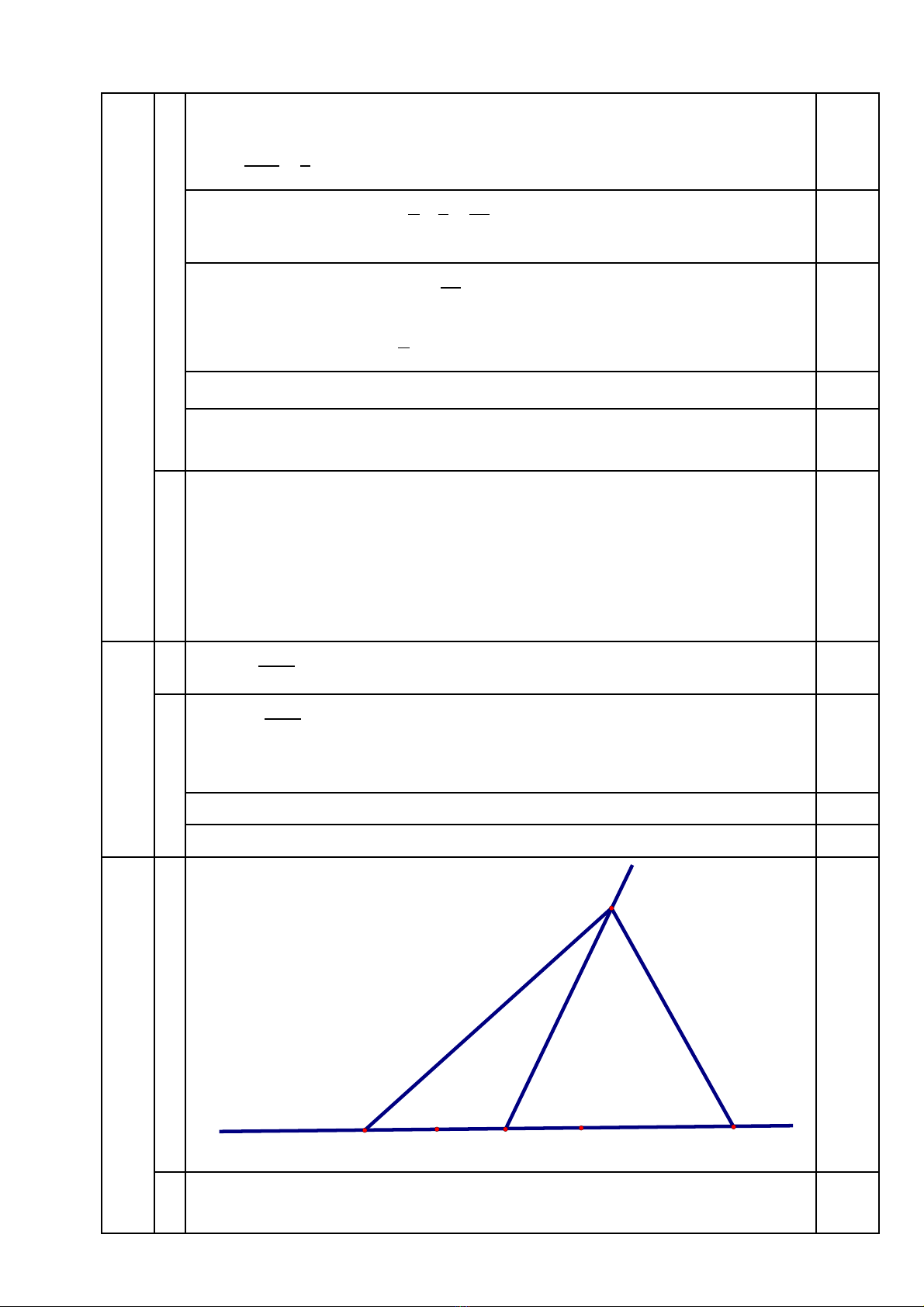
4
x
y
A
B
D
C
K
K
0.5
1 Vì B thu c tia Ax, D thu c tia đi c a tia Axộ ộ ố ủ
A n m gi a D và Bằ ữ
0.5
BD = BA + AD = 6 + 4 = 10 (cm) 0.75
KL:….. 0.25
2 Vì A n m gi a D và B => Tia CA n m gi a 2 tia CB và CDằ ữ ằ ữ 0.5
ﾷ
ﾷ
ﾷ
ﾷ
ﾷ
ﾷ
0 0 0
80 45 35
ACD ACB BCD
ACD BCD ACB
+ =�
= − = − =�
0,5
0,5
KL:…. 0.25
3 * Tr ng h p 1 : K thu c tia Axườ ợ ộ
- L p lu n ch ra đc K n m gi a A và Bậ ậ ỉ ượ ằ ữ 0.25
- Suy ra: AK + KB = AB 0.25
KB = AB – AK = 6 – 2 = 4 (cm) 0.5
* Tr ng h p 2 : K thu c tia đi c a tia Axườ ợ ộ ố ủ
- L p lu n ch ra đc A n m gi a K và Bậ ậ ỉ ượ ằ ữ 0.25
- Suy ra: KB = KA + AB 0.25
KB = 6 + 2 = 8 (cm) 0.25
* K t lu n: V y KB = 4 cm ho c KB = 8 cmế ậ ậ ặ 0.5
5Vì x và y là nguyên t và 5x + y và xy + 13 cũng là các s nguyên tố ố ố
Nên 5x + y và xy + 13 là các s nguyên t l n h n 3 ố ố ớ ơ
5x + y và xy + 13
là các s l ố ẻ
xy ch n ẵ
x ho c y ch n.ặ ẵ 0.25
* N u x ch n mà x là s nguyên t ế ẵ ố ố
x=2
10+y và 2y+13 là số
nguyên t .ố
N u yế
3M
mà y nguyên t ố
y=3 ta có 10+y =13 và 2y+13=19 d uề
là nguyên t . V y x=2 và y=3ố ậ
N u y không chia h t cho 3 ế ế
y=3k+1 ho c y=3k +2ặ
+V i x= 3k+1 ta có 2y+13=6k+15 ớ
3M
mà 2y+13>3 nên 2y+13 không
nguyên t .ố
+V i x= 3k+2 ta có 10+y=3k+12 ớ
3M
mà 10+y>3 nên 10+y không nguyên
t .ố
V y x=2 và y=3ậ
0.25
0.25
* N u y ch n l p luân tế ẵ ậ ng t ta có x=3 và y=2 tho mãnươ ự ả
KL 0.25