TR NG THCS VINH QUANGƯỜ
T : T nhiênổ ự Đ THI HSG C P TR NGỀ Ấ ƯỜ
Môn: TOÁN - L p 9ớ
Đ s 1ề ố
Th i gian 90 phút ờ(Không k giao đ )ể ề
Câu 1: (2 đi m)ể Các bi u th c sau có th âm đ c không? Có th b ng 0 đ cể ứ ể ượ ể ằ ượ
không?
A = 4x4 – 4x3 + x2
B = 2x2 – 2x + 1
Câu 2: (2 đi m) ểCho hai s có t ng b ng và hi u b ng tìm tích hai s y?ố ổ ằ ệ ằ ố ấ
Câu 3: (2 đi m) ểCho A = .
a) Rút g n bi u th c Aọ ể ứ
b) Tìm giá tr c a x đ A> -6 ị ủ ể
Câu 4: (3 đi m) ểCho tam giác ABC vuông t i A, đ ng cao AH. G i M là hìnhạ ườ ọ
chi u c a H trên AB, N là hình chi u c a H trên AC.ế ủ ế ủ
a) Ch ng minh r ng AM.AB = AN.ACứ ằ
b) Tam giác vuông ABC có thêm đi u ki n gì thì t giác AMHN có di n tích l nề ệ ứ ệ ớ
nh t? Bi t BC = a (Không đ i). ấ ế ổ
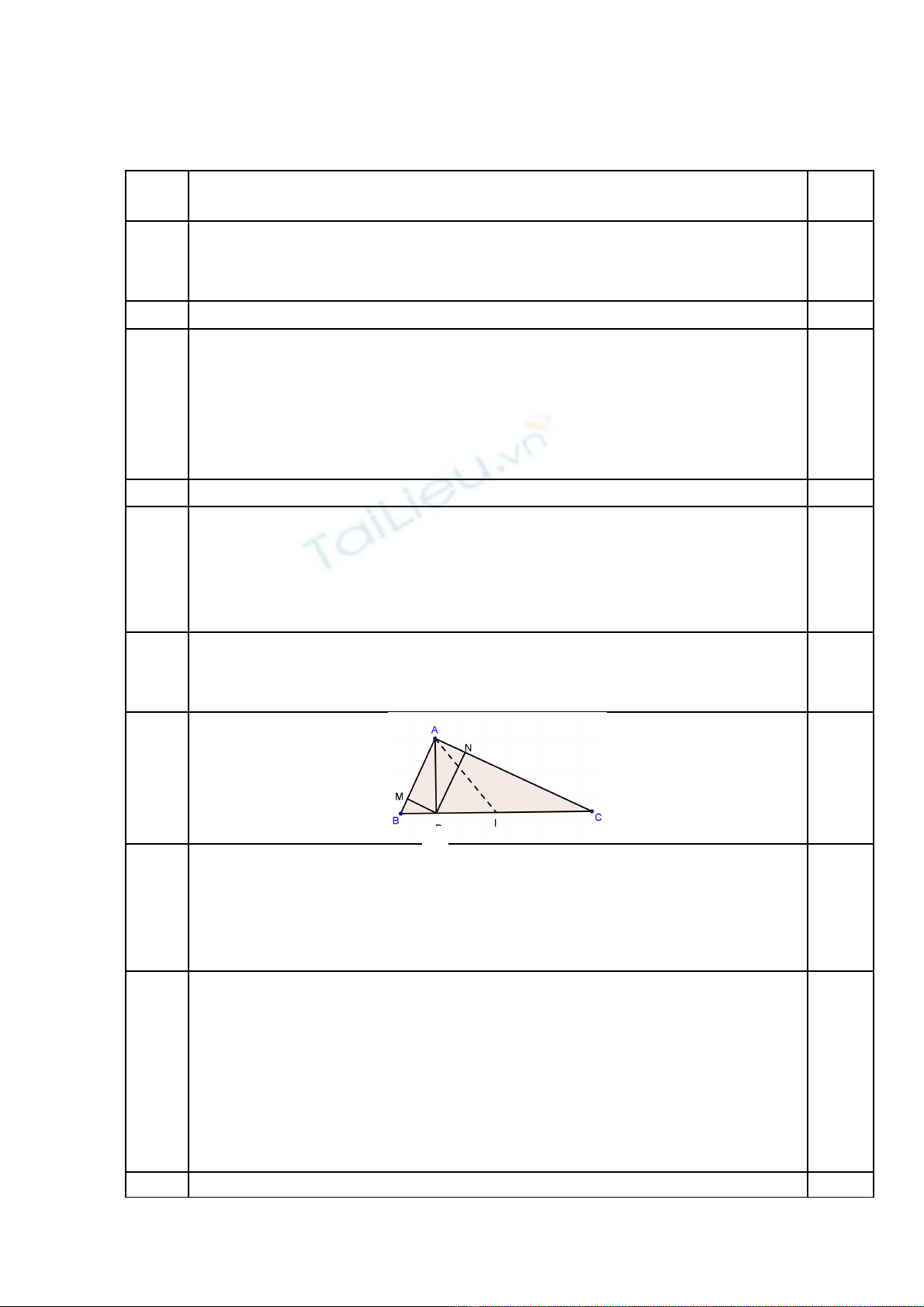
Câu 5: (1 đi m) ểM t ng i đo chi u cao AB b ng cách ng mộ ườ ề ằ ắ
t C (Hình v ). Tính đ dài AB bi t CH = 1,5m, = 45ừ ẽ ộ ế 0,
= 150.
TR NG THCS VINH QUANGƯỜ
T : T nhiênổ ự Đ THI HSG C P TR NGỀ Ấ ƯỜ
Môn: TOÁN - L p 9ớ
Đ s 2ề ố
Th i gian 90 phút ờ(Không k giao đ )ể ề
Câu 1: (1 đi m) ểTìm ch sai trong bài toán Ng y bi n sau: ỗ ụ ệ
a2 – 2ab +b2 = b2 – 2ab + a2
(a – b)2 = (b – a)2
a – b = b – a
2a = 2b
a = b
Câu 2: (2 đi m) ểCho hai s không âm a và b. G i trung bình nhân c a hai s là .ố ọ ủ ố
Ch ng minh r ng trung bình c ng c a hai s không nh h n trung bình nhân?ứ ằ ộ ủ ố ỏ ơ
(BĐT CôSi)
Câu 3: (3 đi m) ểCho bi u th c ể ứ
2 2
2 2
x + x -4x x - x -4x
A = -
x - x -4x x + x - 4x
.
a) Tìm đi u ki n c a x đ A có nghĩa.ề ệ ủ ể
b) Rút g n bi u th c A.ọ ể ứ
c) Tìm giá tr c a x đ A < ị ủ ể
Câu 4: (2 đi m) ểCho tam giác nh n ABC, BC = a, AC = b, AB = c. ọ
Ch ng minh r ng = = .ứ ằ
Câu 5: (2 đi m) ểCho hình bình hành ABCD có AB = a, AD = b (a>b), = α < 900.
Các tia phân giác c a các góc A, B, C, D c t nhau t o thành m t t giác.ủ ắ ạ ộ ứ
a) T giác đó là hình gì?ứ
b) Tính di n tích t giác đó theo a, b, ệ ứ α.
H NG D N CH MƯỚ Ẫ Ấ
Đ 1Ề
Câu Đáp án Điể
m
1
1a
A = 4x4 – 4x3 + x2 = x2(4x2- 4x + 1) = x2(2x-1)2
A = x2(2x-1)2≥ 0 ∀ x∈ R
A = 0 ⇔ 2x - 1 = 0 ⇔ x =
1
1b B = 2x2 – 2x + 1 = x2 + x2 - 2x + 1 = x2 + (x - 1)2 > 0 ∀ x∈ R 1
2G i hai s là a và b ta có a + b = và a - b = ọ ố
V y a = = ; b = = ậ
⇒ a.b = . = = = 1
0,5
1
0,5
3A = . Đi u ki n 0 < x ề ệ ≠ 1
3a Rút g n: ọ
Đ t = a ta cóặ
A = . = .
= = = = -2a
V y A = -2 ậ
1
3b A = -6 ⇔ x = 1
A > -6 ⇔ < 3 ⇔ x < 9
V y đ A > - 6 thì ậ ể
1
40,5
4a Trong tam giác vuông AHB ta có:
AM.AB = AH2 (1)
Trong tam giác vuông AHC ta có:
AN.AC = AH2 (2)
T (1)&(2) ừ⇒ AM.AB = AN.AC
0,5
0,5
4b SAMHN = AM.AN = . = =
G i I là trung đi m c a BC ta có:ọ ể ủ
AH ≤ AI = = nên SAMHN ≤ =
Do đó Max SAMHN = ⇔ H ≡ I ⇔ ∆ABC vuông cân t i A ạ
0,5
0,5
0,5
5
H
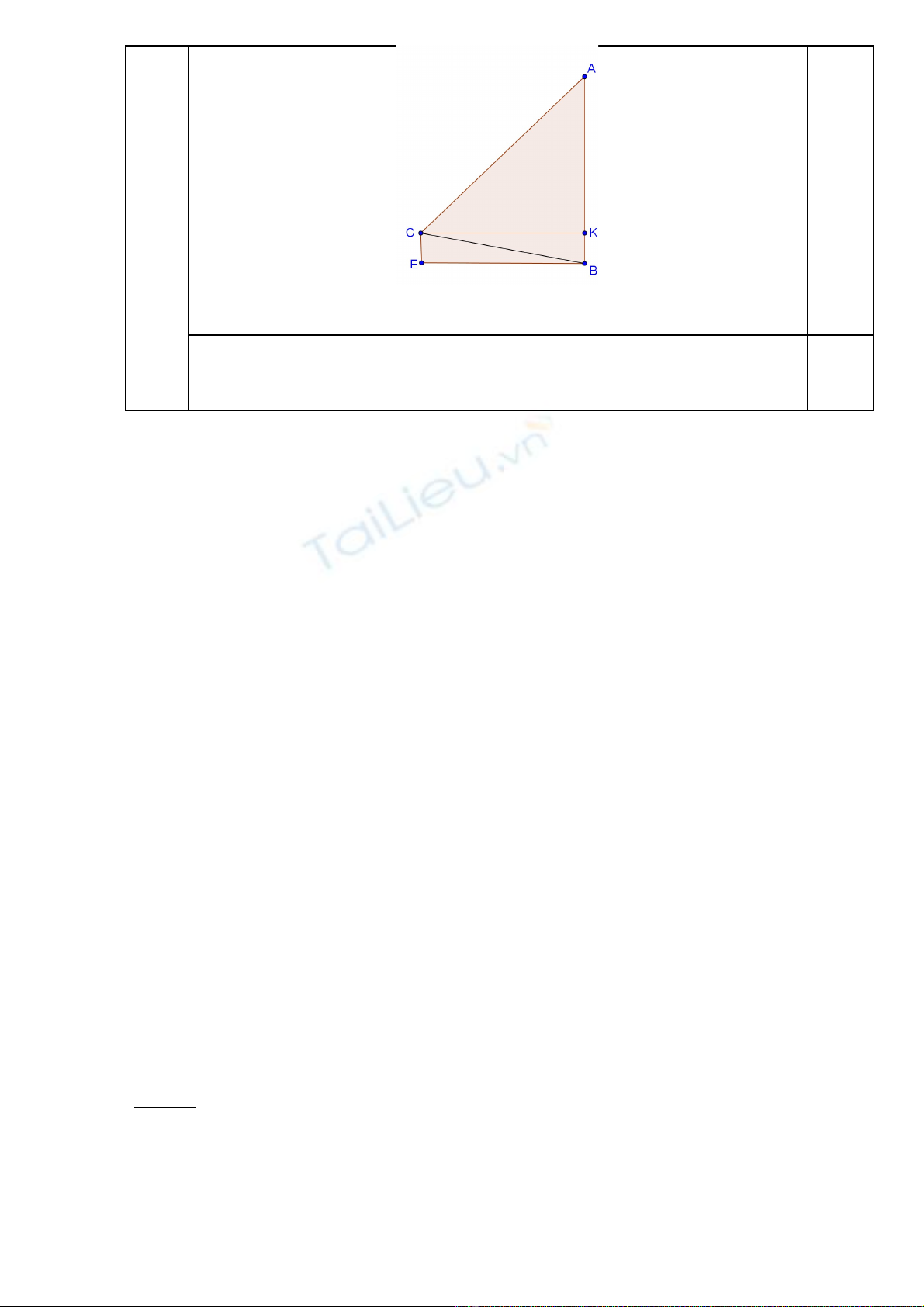
Ta có: KC = KB.Cotg 150 = 1,5.3,732 = 5,6 (m).
KA = KC = 5,6 (m).
AB = KA + KB = 5,6 + 1,5 = 7,1 (m)
1
TR NG THCS VINH QUANGƯỜ
T : T nhiênổ ự Đ THI HSG C P TR NGỀ Ấ ƯỜ
Môn: TOÁN - L p 9ớ
Đ s 2ề ố
Th i gian 90 phút ờ(Không k giao đ )ể ề
Câu 1: (1 đi m) ểTìm ch sai trong bài toán Ng y bi n sau: ỗ ụ ệ
a2 – 2ab +b2 = b2 – 2ab + a2
(a – b)2 = (b – a)2
a – b = b – a
2a = 2b
a = b
Câu 2: (2 đi m) ểCho hai s không âm a và b. G i trung bình nhân c a hai s là .ố ọ ủ ố
Ch ng minh r ng trung bình c ng c a hai s không nh h n trung bình nhân?ứ ằ ộ ủ ố ỏ ơ
(BĐT CôSi)
Câu 3: (3 đi m) ểCho bi u th c ể ứ
2 2
2 2
x + x -4x x - x -4x
A = -
x - x -4x x + x - 4x
.
a) Tìm đi u ki n c a x đ A có nghĩa.ề ệ ủ ể
b) Rút g n bi u th c A.ọ ể ứ
c) Tìm giá tr c a x đ A < ị ủ ể
Câu 4: (2 đi m) ểCho tam giác nh n ABC, BC = a, AC = b, AB = c. ọ
Ch ng minh r ng = = .ứ ằ
Câu 5: (2 đi m) ểCho hình bình hành ABCD có AB = a, AD = b (a>b), = α < 900.
Các tia phân giác c a các góc A, B, C, D c t nhau t o thành m t t giác.ủ ắ ạ ộ ứ
a) T giác đó là hình gì?ứ
b) Tính di n tích t giác đó theo a, b, ệ ứ α.
Câu Đáp án Điể
m
1Sai l m trong bài là:ầ
(a – b)2 = (b – a)2
=
Vì th không th suy ra a-b = b-a ế ể
0.5
0.5
2Ta có BĐT: = (1) V i a ớ≥ 0; b ≥ 0
(1) ⇔ 2≥ ab ⇔ ≥ ab ⇔ a2+2ab+b2≥ 4ab
⇔ a2- 2ab + b2≥ 0⇔(a+b)2≥0 (Đúng v i m i a, b)ớ ọ
Đ ng th c x y ra khi a = b.ẳ ứ ả
0.5
0.5
0.5
0.5
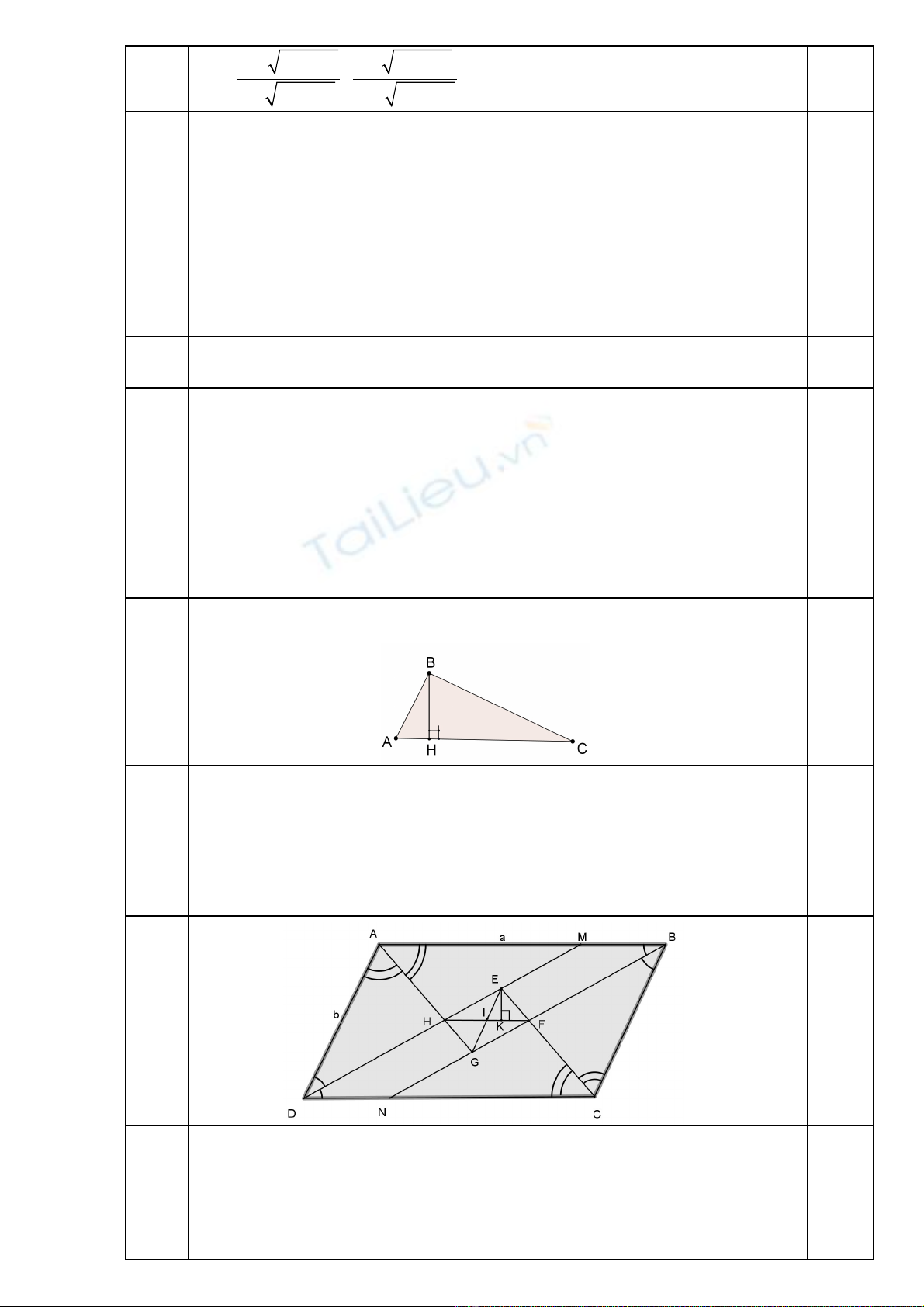
3
2 2
2 2
x + x -4x x - x -4x
A = -
x - x -4x x + x - 4x
3a Đi u ki n đ A có nghĩa:ề ệ ể
* x2-4x≥0⇔x(x-4)≥0⇔ ⇔ ⇔ x≥4 (1)
* Xét x2 = 2 ⇔ x2 = x2 - 4x ⇔ 4x = 0 ⇔ x = 0
Do đó v i xớ≠0 thì x≠ ± (2)
(1)(2) ⇒ v i xớ≥4 thì A có nghĩa.
0.25
0.25
0.25
0.25
3b Rút g n:ọ
A = = =
1
3c Gi i Bpt: ả
<
⇔ x2-4x-5<0
⇔x2+x-5x-5<0
⇔x(x+1)-5(x+1)<0
⇔(x+1)(x-5)<0
⇔ ⇔
K t h p hai đi u ki n trên ta có: -1<x<5 thì A<ế ợ ề ệ
1
40.5
K AH ẻ⊥ BC ta có: = : = ⇒ =
T ng t : = ươ ự
V y: = = ậ
0.5
0.5
0.5
50.25
5a Ta có: AB // CD, AG và DM là phân giác c a hai góc trong cùngủ
phía đ i v i AD nên AG ố ớ ⊥ DM = H.
T ng t : AG ươ ự ⊥ BN = G
T ng t có: CE ươ ự ⊥ BN = F
T ng t : CE ươ ự ⊥ DM = E
0.75