S GD&ĐT VĨNH PHÚCỞ
Đ CHÍNH TH CỀ Ứ
K THI CH N HSG L P 10 THPT NĂM H C 201Ỳ Ọ Ớ Ọ 4-2015
Đ THI MÔN: ỀTOÁN
(Dành cho h c sinh THPT không chuyên)ọ
Th i gian làm bài: 180 phút, không k th i gian phát đờ ể ờ ề
Câu 1 (2,0 đi m).ể
Tìm t p xác đnh c a hàm s : ậ ị ủ ố
( )
2 2
2014 2015
2 3 2
= +
− + + −
f x
x x x x
.
Câu 2 (1,0 đi m). ể
a) Ch ng minh r ng hàm s ứ ằ ố
( )
1
x
f x x
=+
đng bi n trên kho ng ồ ế ả
( )
1;
− +
.
b) Ch ng minh r ng hàm s ứ ằ ố
( )
2015 2015= − − +f x x x
là m t hàm s l .ộ ố ẻ
Câu 3 (1,0 đi m).ể
Gi i ph ng trình: ả ươ
2
19 3 4 6 6 2 12 3+ + − − + = − + +x x x x x
.
Câu 4 (1,0 đi m).ể
Gi i h ph ng trình: ả ệ ươ
2 2
2 2
2 3 1 0
3 0
x y xy y
x y y
+ − − − =
+ − − =
Câu 5 (1,0 đi m).ể
Tìm t t c các giá tr c a ấ ả ị ủ
m
sao cho b t ph ng trình ấ ươ
( ) ( )
2
1 2 2 2 2 0− + + + + m x m x m
vô
nghi m (ệx là n, ẩm là tham s ).ố
Câu 6 (1,0 đi m).ể
Cho tam giác ABC không cân n i ti p đng tròn tâm ộ ế ườ O và G là tr ng tâm c a tam giác ọ ủ ABC.
G i ọM, N, P l n l t là tr ng tâm tam giác ầ ượ ọ OBC, OCA, OAB và G’ là tr ng tâm tam giác ọMNP.
Ch ng minh r ng ứ ằ O, G, G’ th ng hàng.ẳ
Câu 7 (1,0 đi m).ể
Cho tam giác ABC không vuông và có các c nh ạ
. Ch ng minh r ngứ ằ
n u tam giác ếABC th a mãn ỏ
2 2 2
2+ =a b c
và
tan tan 2 tan
+ =
A C B
thì tam giác ABC đu.ề
Câu 8 (1,0 đi m).ể
Trong m t ph ng v i h t a đ ặ ẳ ớ ệ ọ ộ
Oxy
, cho tam giác ABC không là tam giác vuông và n i ti pộ ế
đng tròn (ườ I) ( đng tròn (ườ I) có tâm là I ); đi m ể
( )
2;2H
là tr c tâm tam giác ựABC. K các đngẻ ườ
kính AM, BN c a đng tròn (ủ ườ I). Tìm t a đ các đnh c a tam giác ọ ộ ỉ ủ ABC bi t ế
( ) ( )
5;3 , 1;3M N
và
đng th ng ườ ẳ BC đi qua đi m ể
( )
4;2P
.
Câu 9 (1,0 đi m).ể
Cho
, ,a b c
là các s th c d ng th a mãn đi u ki n ố ự ươ ỏ ề ệ
2015
+ + =
a b c
. Ch ng minh r ng:ứ ằ
2 2 2
2015 2015 2015 2015 2015 2015
6 2 2 � �
− − − − − −
+ + + + +
� �
� �
� �
a a b b c c a b c
bc ca ab a b c
.
-------------H t-------------ế
Thí sinh không đc s d ng tài li u.ượ ử ụ ệ
Cán b coi thi không gi i thích gì thêm.ộ ả
H và tên thí sinh:…………………….………..…….…….….….; S báo danh……………………ọ ố
S GD&ĐT VĨNH PHÚCỞK THI CH N HSG L P 10 THPT NĂM H C 201Ỳ Ọ Ớ Ọ 4-2015
ĐÁP ÁN MÔN: TOÁN
(Dành cho h c sinh THPT không chuyên)ọ
I. L U Ý CHUNG:Ư
- H ng d n ch m ch trình bày m t cách gi i v i nh ng ý c b n ph i có. Khi ch m bài h c sinhướ ẫ ấ ỉ ộ ả ớ ữ ơ ả ả ấ ọ
làm theo cách khác n u đúng và đ ý thì v n cho đi m t i đa.ế ủ ẫ ể ố
- Đi m toàn bài tính đn 0,25 và không làm tròn.ể ế
- V i bài hình h c n u thí sinh không v hình ph n nào thì không cho đi m t ng ng v i ph n đó.ớ ọ ế ẽ ầ ể ươ ứ ớ ầ
II. ĐÁP ÁN:
Câu N i dung trình bàyộĐi mể
1 (2,0 đi m)ể
Hàm s ố
( )
f x
xác đnh khi và ch khi ị ỉ
2
2
2 3 0
2 0
x x
x x
− + + >
− >
1,0
1 3
2
0
x
x
x
− < <
>
<
0,5
2 3
1 0
x
x
< <
− < <
. V y t p xác đnh c a hàm s ậ ậ ị ủ ố
( )
f x
là
( ) ( )
1;0 2;3S= − U
0,5
2 (1,0 đi m)ể
a.(0,5 đi m)ể
V i m i ớ ọ
( )
1 2 1 2
, 1; ,x x x x− +� � �
ta có:
( ) ( )
1 2
1 2 1 2
1 2 1 2
1 1
x x
f x f x x x
Kx x x x
−
−+ +
= =
− −
0,25
( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
1 2 2 1 1 2
1 2 1 2 1 2 1 2 1 2
1 1 10
1 1 1 1 1 1
x x x x x x
x x x x x x x x x x
+ − + −
= = = >
− + + − + + + +
(Do
( )
1 2
, 1;x x − +� �
).
Do đó
( )
0K f x>
đng bi n trên ồ ế
( )
1;− +
.
0,25
b.(0,5 đi m)ể
T p xác đnh c a hàm s là ậ ị ủ ố
[ ]
2015;2015D= −
. V i m i ớ ọ
x D
, ta có
x D
−
,0,25
( )
( )
( )
2015 2015 2015 2015f x x x x x f x− = + − − = − − − + = −
suy ra
( )
f x
là hàm s l .ố ẻ 0,25
3 (1,0 đi m)ể
Đi u ki n xác đnh: ề ệ ị
2
6 0
2 0 3 2
3 0
x x
x x
x
− − +
− −�� ��
+
.
B t ph ng trình đã cho t ng đng v i:ấ ươ ươ ươ ớ
0,25
(Đáp án có 05 trang)
( ) ( )
( )
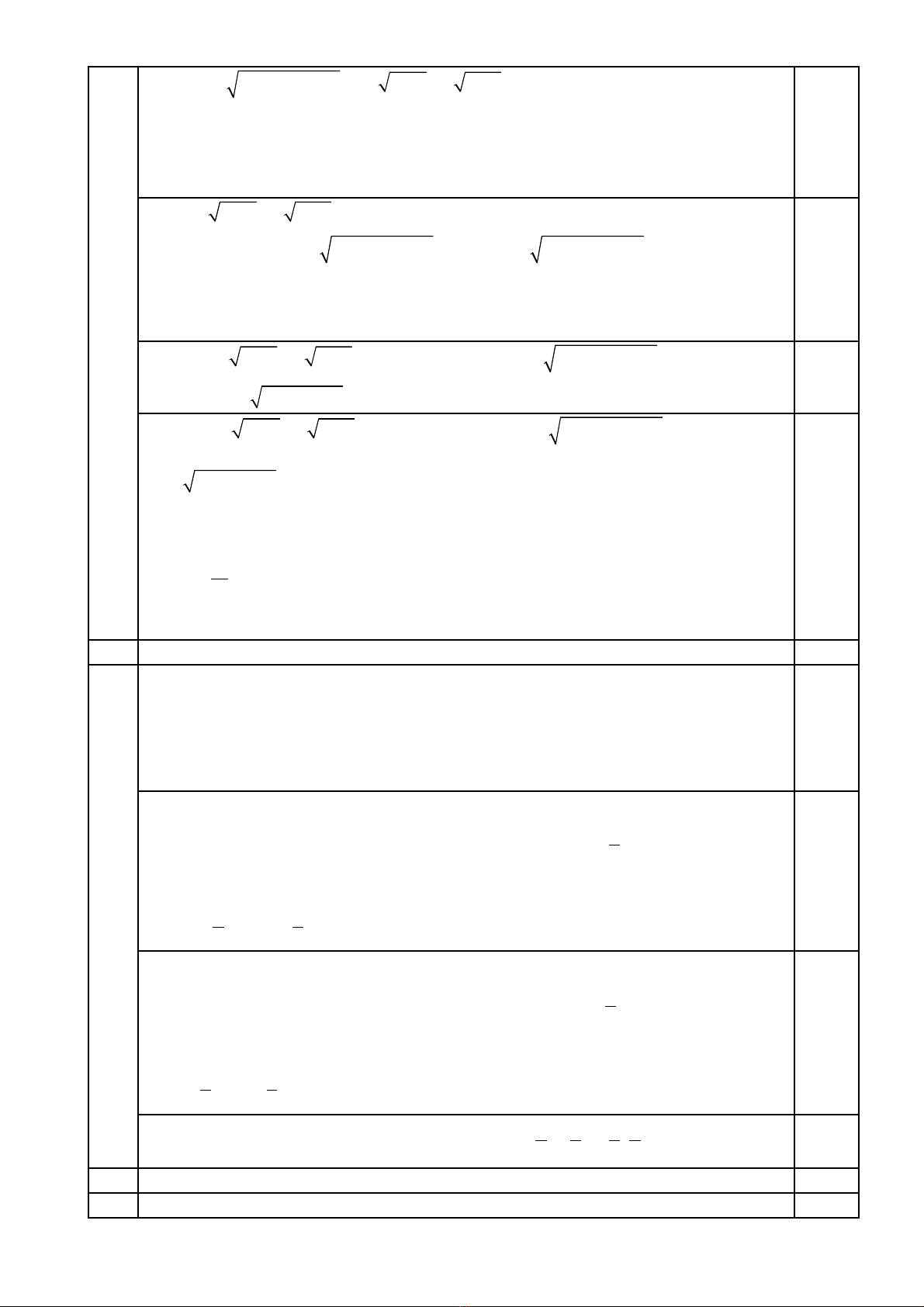
19 3 4 2 3 6 2 2 3x x x x x+ + − + = − + +
Đt ặ
2 2 3 , 0t x x t= − + + >
ta có:
( ) ( ) ( ) ( ) ( )
2
2 4 3 4 2 3 14 3 4 2 3t x x x x x x x= − + + + − + = + + − +
Thay vào ph ng trình trên ta đc: ươ ượ
2 2
1
5 6 6 5 0 5
t
t t t t t
=
+ = − + =� � =
0,25
+)
( ) ( ) ( )
1 2 2 3 1 2 4 3 4 2 3 1t x x x x x x= − + + = − + + + − + =� �
2
3 13 4 6 0x x x+ + − − + =�
vô nghi m do ệ
3 2x−
0,25
+)
( ) ( ) ( )
5 2 2 3 5 2 4 3 4 2 3 25t x x x x x x= − + + = − + + + − + =� �
( )
( )
2
2
2
16 6 11 3
4 6 11 3
11 3 0
x x x
x x x
x
− − + = −
− − + = −� � −
2
25 50 25 0
1
11
3
x x
x
x
− + =
=� �
th a mãn đi u ki n. ỏ ề ệ
V y t p nghi m c a ph ng trình đã cho là ậ ậ ệ ủ ươ
{ }
1S=
.
0,25
4 (1,0 đi m)ể
( )
( ) ( )
2 2
2 2
2 3 1 0 1
3 0 2
x y xy y I
x y y
+ − − − =
+ − − =
Ta có
( ) ( ) ( )
1
1 1 2 1 0 2 1
x y
x y x y x y
= −
− + − − =� � = +
0,25
V i ớ
1x y= −
thay vào (2) ta đc ượ
2
2
2 3 2 0 1
2
y
y y y
=
− − = = −
+)
2 1y x= =�
.
+)
1 3
2 2
y x= − = −�
.
0,25
V i ớ
2 1x y= +
thay vào (2) ta đc ượ
2
1
5 3 2 0 2
5
y
y y y
= −
+ − = =
+)
1 1y x= − = −�
.
+)
2 9
5 5
y x= =�
.
0,25
V y, h (ậ ệ I) có nghi m ệ
( )
;x y
là:
( ) ( )
3 1 9 2
1; 2 , 1; 1 , ; , ;
2 2 5 5
� �� �
− − − −
� �� �
� �� �
.0,25
5 (1,0 đi m)ể
B t ph ng trình đã cho vô nghi m khi và ch khiấ ươ ệ ỉ 0,25
( ) ( )
2
1 2 2 2 2 0m x m x m x− + + + + < ∀ ﾡ
TH1. N u ế
1m=
thì
2
6 4 0, ,
3
x x x x+ < ∀ < − ∀�� �ﾡ ﾡ
vô lí.0,25
TH2. N u ế
1m
thì
( ) ( )
2
1 2 2 2 2 0m x m x m x− + + + + < ∀ ﾡ
( ) ( ) ( )
22
1 0 1
4 6 0
' 2 1 2 2 0
mm
m m
m m m
− <
<
� �
− + + <
∆ = + − − + <
0,25
1
2 10
2 10
2 10
m
m
m
m
<
< −� �
> +
< −
.
V y t p h p các giá tr c a ậ ậ ợ ị ủ
m
là
( )
;2 10S= − −
.
0,25
6 (1,0 đi m) Bài này h c sinh không nh t thi t ph i v hình.ể ọ ấ ế ả ẽ
K t qu c b n: cho tam giác ế ả ơ ả ABC tr ng tâm ọG. Khi đó v i m i đi m ớọểO ta có
3.OA OB OC OG+ + =
uuur uuur uuur uuur
.
Do M, N, P l n l t là tr ng tâm các tam giác ầ ượ ọ OBC, OCA, OAB nên:
3.OB OC OM+ =
uuur uuur uuuur
3.OC OA ON+ =
uuur uuur uuur
3.OA OB OP+ =
uuur uuur uuur
0,5
C ng t ng v 3 h th c trên ta đc: ộ ừ ế ệ ứ ượ
( ) ( )
2 3OA OB OC OM ON OP+ + = + +
uuur uuur uuur uuuur uuur uuur
2.3. 3.3. ' 2. 3. ' , , 'OG OG OG OG O G G= =� � �
uuur uuuur uuur uuuur
th ng hàng.ẳ0,5
7 (1,0 đi m)ể
Theo đnh lí hàm s sin và côsin ta có: ị ố
( )
2 2 2 2 2 2
sin 2
tan cos
2
a
A abc
R
Ab c a
AR b c a
bc
= = =
+ − + −
0,25
T ng t ta có ươ ự
( ) ( )
2 2 2 2 2 2
tan , tan
abc abc
B C
R c a b R a b c
== =
+ − + −
.
( ) ( ) ( )
2 2 2 2 2 2 2 2 2
tan tan 2.tan 2.
abc abc abc
A C B R b c a R a b c R a c b
+ = + =� � + − + − + −
0,25
2 2 2 2 2 2 2 2 2
1 1 1
2.
b c a a b c a c b
+ =�+ − + − + −
( ) ( ) ( ) ( )
2 2 2 2 2 2 2 2 2 2 2 2
c a b a b c b c a a c b+ − + − + + − + −�
( ) ( )
2 2 2 2 2 2
2b c a a b c= + − + −
( ) ( ) ( )
()
2 2 2
4 2 2 4 2 2 4 2 2
2a b c c a b b a c− − + − − = − −�
0,25
( ) ( ) ( )
2 2 2 2 2 2 2 2
2 2 0a a b c c b c b b c+ − + − + = =� �
(do
2 2 2
2a b c+ =
),
k t h p v i ế ợ ớ
2 2 2
2a b c a b c+ = = =�
.
V y tam giác ậABC đu.ề
0,25
8 (1,0 đi m)ể
Nh n xét.ậ Các t giác ứBHCM, AHCN là các hình bình hành suy ra n u g i ế ọ E, F l n ầ
l t là trung đi m c a ượ ể ủ BC, CA thì E, F cũng t ng ng là trung đi m c a ươ ứ ể ủ HM, HN.
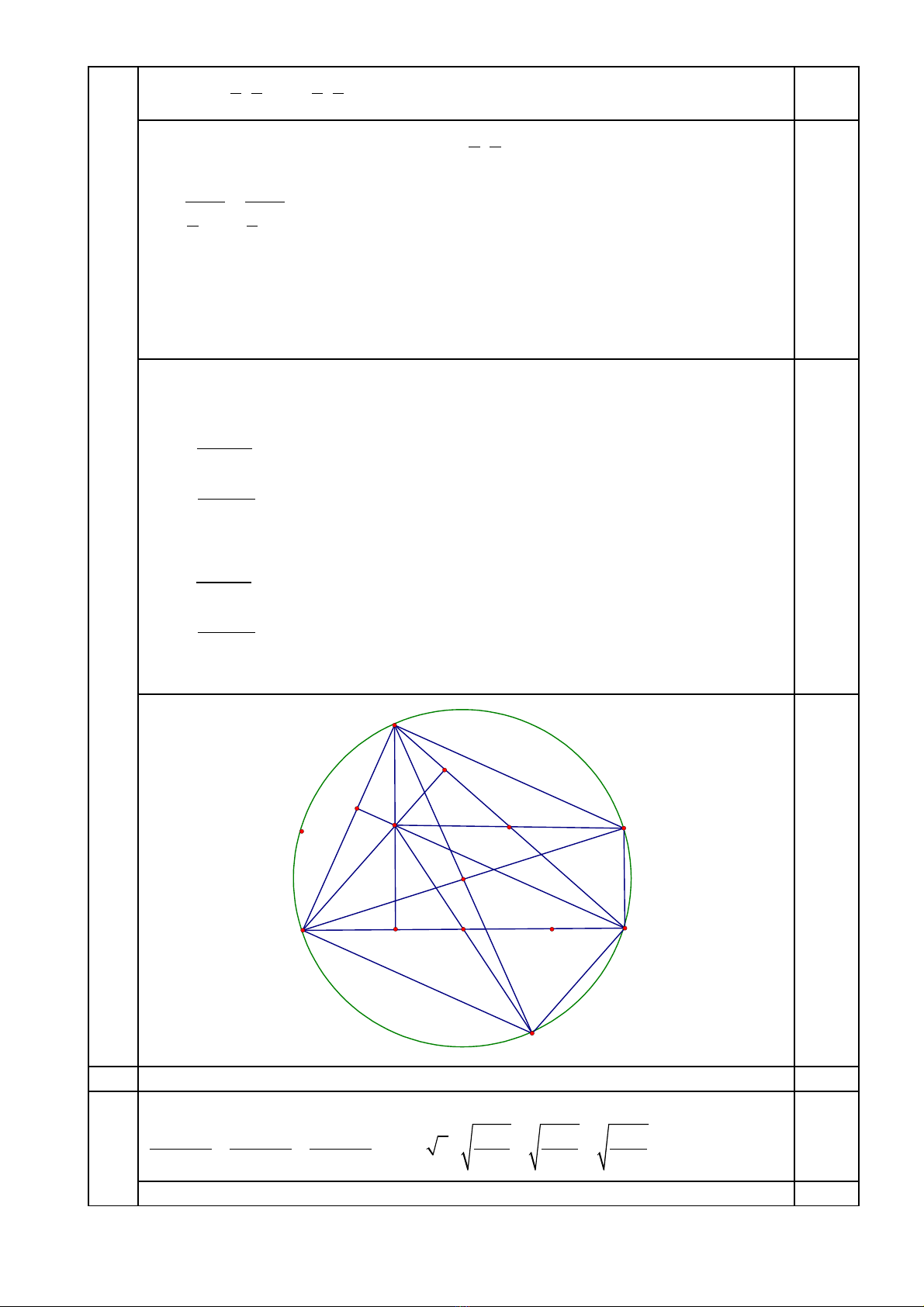
Do đó
7 5 3 5
; , ;
2 2 2 2
M N
� � � �
� � � �
� � � �
.
Đng th ng ườ ẳ BC đi qua đi m P(4;2), ể
7 5
;
2 2
M� �
� �
� �
nên:
4 2
: 6 0
7 5
4 2
2 2
x y
BC x y
− −
= + − =�
− −
.
AH vuông góc v i ớBC suy ra AH có vtpt
( )
1; 1
AH
n= −
r
, k t h p v i ế ợ ớ AH đi qua đi mể
( )
2;2H
suy ra:
( ) ( )
:1 2 1 2 0 0AH x y x y− − − = − =�
.
0,25
( ) ( )
; , ; 6A AH A a a C BC C b b−� � � �
.
Do F là trung đi m ểAC nên:
( ) ( )
3 1
21;1 , 2;4
6 5 2
2
A C
F
A C
F
x x
xa b a A C
y y a b b
y
+
=
+ = =
� �
� � �
� � �
+ + − = =
� �
=
.
Do E là trung đi m c a ể ủ BC nên:
( )
25
25;1 .
2 1
2
B C
E
B E C B
B C B E C B
E
x x
xx x x xB
y y y y y y
y
+
=
= − =
� � �
� � �
+ = − =
=
V y ậ
.
0,5
F
E
H
P
I
N
M
C
B
A
0,25
9 (1,0 đi m)ể
Thay
2015 a b c
= + +
thì b t đng th c c n ch ng minh có d ng:ấ ẳ ứ ầ ứ ạ
( ) ( ) ( )
6 2 2
a b c b c a c a b b c c a a b
bc ca ab a b c
� �
+ + + + + +
+ + + + +
� �
� �
� �
0,25
Ta có0,5