
SỞ GIÁO DỤC VÀ ĐÀO TẠO
NAM ĐỊNH
ĐỀ THI CHỌN HỌC SINH GIỎI NĂM HỌC 2015-2016
Môn: TOÁN – Lớp 9
Thời gian làm bài: 150 phút
(Đề thi gồm 01 trang)
Câu 1. (3,0 điểm)
1. Tính giá trị biểu thức
5 3 5 3 11 6 2
5 22
P
.
2. Cho các số thực x, y, z thỏa mãn đồng thời các điều kiện
2,x y z
2 2 2 18x y z
và
1xyz
.
Tính giá trị của
1 1 1
111
Sxy z yz x zx y
Câu 2. (5,0 điểm)
1. Giải phương trình
2 2 1 3 5 11 0x x x
.
2. Giải hệ phương trình
2
22
1 1 1 0
7 3 0.
y y x x
x y x
Câu 3. (3,0 điểm)
1. Tìm tất cả các số nguyên x, y thỏa mãn
22 1x y xy x y
.
2. Chứng minh với mọi số nguyên dương n lớn hơn 1 ta có
2 3 4... 1 3nn
.
Câu 4. (7,0 điểm) Cho tam giác nhọn ABC có
AB AC
, nội tiếp đường tròn
O
và ngoại tiếp đường tròn
I
. Điểm D thuộc cạnh AC sao cho
ABD ACB
. Đường thẳng AI cắt đường tròn ngoại tiếp tam giác DIC
tại điểm thứ hai là E và cắt đường tròn
O
tại điểm thứ hai là Q. Đường thẳng đi qua E và song song với AB
cắt BD tại P.
1. Chứng minh tam giác QBI cân;
2. Chứng minh
..BP BI BE BQ
;
3. Gọi J là tâm đường tròn nội tiếp tam giác ABD, K là trung điểm của JE. Chứng minh
//PK JB
.
Câu 5. (2,0 điểm) Cho một lớp học có 35 học sinh, các học sinh này tổ chức một số câu lạc bộ môn học. Mỗi
học sinh tham gia đúng một câu lạc bộ. Nếu chọn ra 10 học sinh bất kì thì luôn có ít nhất 3 học sinh tham gia
cùng một câu lạc bộ. Chứng minh có một câu lạc bộ gồm ít nhất 9 học sinh.
----------Hết----------
Họ và tên thí sinh:………………………Họ, tên chữ ký GT1:…………………………………..
Số báo danh:…………………………… Họ, tên chữ ký GT2:…………………………………..
ĐỀ CHÍNH THỨC

SỞ GIÁO DỤC VÀ ĐÀO TẠO
NAM ĐỊNH
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM THI
KỲ THI CHỌN HSG NĂM HỌC 2015-2016
Môn: TOÁN – Lớp 9
Câu
Đáp án
Điểm
1.1
(1,5)
Tính giá trị biểu thức
5 3 5 3 11 6 2
5 22
P
.
Đặt
5 3 5 3
5 22
M
. Ta có
210 2 22 2
5 22
M
0,5
2M
(Do
0M
)
0,25
2
11 6 2 3 2 3 2
0,5
Suy ra
3P
0,25
1.2
(1,5)
Cho các số thực x, y, z thỏa mãn đồng thời các điều kiện
2,x y z
2 2 2 18x y z
và
1xyz
. Tính giá trị của
1 1 1
111
Sxy z yz x zx y
.
Ta có
1 1 1 1xy z xy x y x y
0,5
Tương tự
1 1 1yz x y z
và
1 1 1zx y z x
0,25
Suy ra
1 1 1 3
1 1 1 1 1 1 1 1 1
x y z
Sx y y z z x x y z
11
1xyz xy yz zx x y z xy yz zx
0,25
Ta có
22 2 2 27x y z x y z xy yz zx xy yz zx
0,25
Suy ra
1
7
S
0,25
2.1
(2,0)
Giải phương trình
2 2 1 3 5 11 0x x x
.
Điều kiện
1
2
x
0,5
2 2 1 3 5 11 0 2 2 1 3 5 11x x x x x x
22
9 1 4 2 5 3 5 11 2 5 3 3x x x x x x x
0,5
2 2 2
33
1
12
2 5 3 9 6 11 12 0
xx
x
x
x x x x x x
0,5
ĐỀ CHÍNH THỨC

Đối chiếu điều kiện ta được
1x
là nghiệm duy nhất của phương trình.
0,5
2.2
(3,0)
Giải hệ phương trình
2
22
1 1 1 0 1
7 3 0 2
y y x x
x y x
.
Điều kiện
1,xy
22
1 1 1 0 1 1 0 1 1 0y y x x y y x y y y x
1
1
y
yx
.
0,5
Với
1y
, thay vào (2) ta được
2 2 2 2 4 2 2
1 7 3 0 1 7 3 2 1 7 3x x x x x x x
2
42
2
11
5 4 0 2
4
xx
xx x
x
(do điều kiện của x)
0,5
Với
1yx
, thay vào (2) ta được
22
1 7 3 0x x x
22
2
4 1 1 7 3 5 0
7 2 2
2
2 2 0
11 7 3 5
x x x
xx
x
xx xx
0,5
2
2
72
1
20
11 7 3 5
x
x
xxx
0,25
Với
2x
suy ra
1y
.
0,5
Ta có
22
72
1 7 1
2 2 1
1 1 1 1
7 3 5 7 3 5
x
xx
xx
xx
2
2
7 3 2 1
211
7 3 5
x
xx
x
Với
1x
thì
2
2
2
7 3 2
7 3 2 0 2 0
7 3 5
x
xx
x
Suy ra
2
2
7 3 2 1
20
11
7 3 5
x
xx
x
0,5
Vậy hệ phương trình có các nghiệm
1;1 , 2;1
.
0,25
3.1
(2,0)
Tìm các số nguyên x, y thỏa mãn
22 1x y xy x y
.
Ta có
2 2 2
22 1 1 1 4x y xy x y x y x y
0,75
Ta có bảng giá trị tương ứng (học sinh có thể xét từng trường hợp)
xy
1x
1y
Nghiệm
;xy
1,0

2
0
0
1;1
-2
0
0
Loại
0
2
0
Loại
0
-2
0
1;1
0
0
2
Loại
0
0
-2
1; 1
Vậy các số
;xy
cần tìm là
1;1
,
1;1
,
1; 1
0,25
3.2
(1,0)
Chứng minh với mọi số nguyên dương n lớn hơn 1 ta có
2 3 4... 1 3nn
.
Với mỗi số nguyên dương k ta có
22
1 1 1 1 1k k k k k
.
0,25
Sử dụng đẳng thức trên liên tiếp với
3,4,...,kn
ta được
3 1 2.4 1 2 1 3.5 1 2 1 3 1 4.6
1 2 1 3 1 1 1 1nn
0,5
2
1 2 1 3 1 1 1 1 2 3 4... 1n n n n
0,25
Ta có điều phải chứng minh.
4
(7,0)
Cho tam giác nhọn ABC có
AB AC
, nội tiếp đường tròn
O
và ngoại tiếp đường
tròn
I
. Điểm D thuộc cạnh AC sao cho
ABD ACB
. Đường thẳng AI cắt đường
tròn ngoại tiếp tam giác DIC tại điểm thứ hai là E và cắt đường tròn
O
tại điểm thứ
hai là Q. Đường thẳng đi qua E và song song với AB cắt BD tại P.
4. Chứng minh tam giác QBI cân;
5. Chứng minh
..BP BI BE BQ
;
6. Gọi J là tâm đường tròn nội tiếp tam giác ABD, K là trung điểm của JE. Chứng minh
//PK JB
.
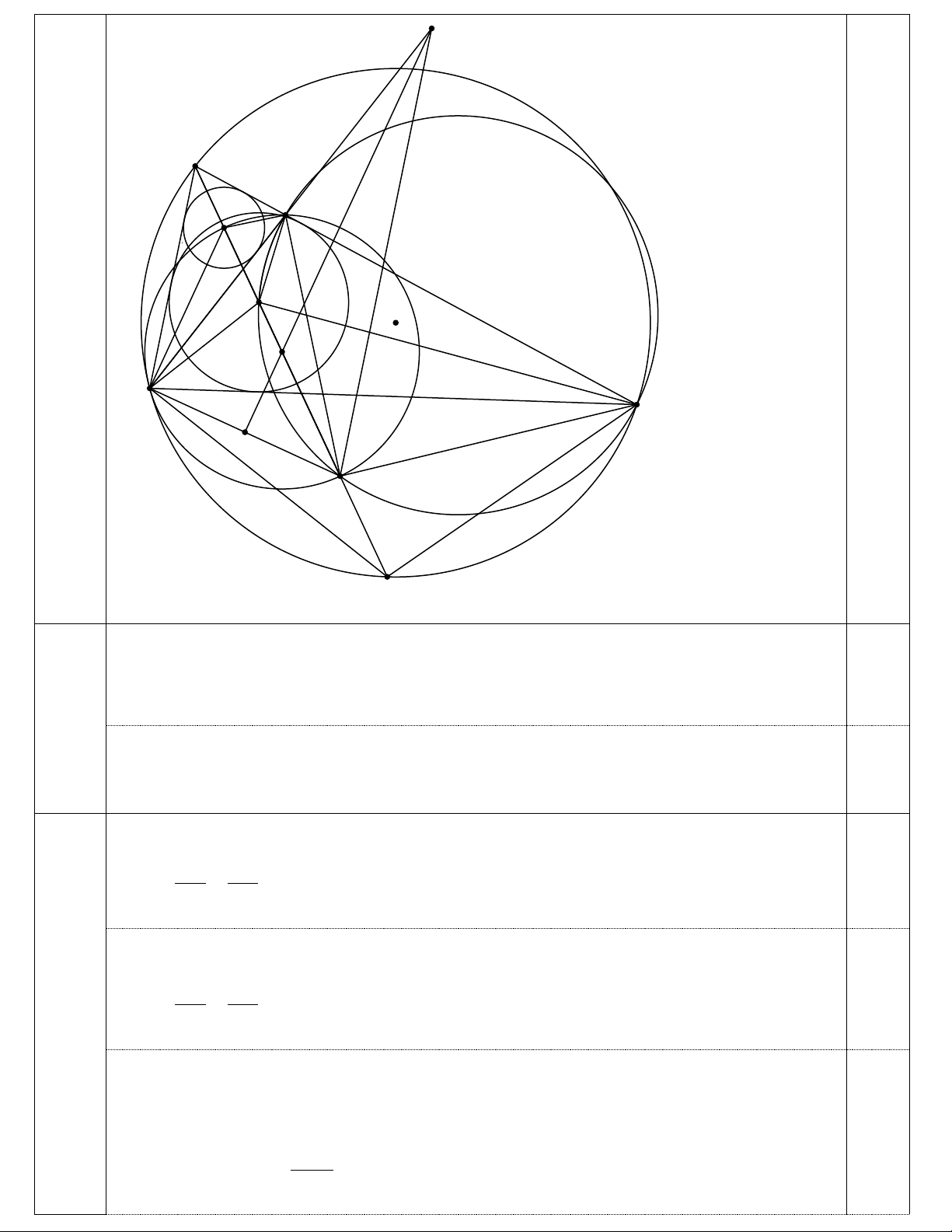
K
H
J
Q
O
P
E
D
I
B
C
A
4.1
(2,0)
Ta có AI là phân giác của
BAC
nên Q là điểm chính giữa của cung BC của (O).
Suy ra
BAQ QAC QBC
1,0
IBQ IBC QBC IBA BAQ BIQ
Hay tam giác QBI cân tại Q.
1,0
4.2
(3,0)
Tam giác ABD đồng dạng tam giác ACB
Suy ra
AB AD
AC AB
hay
2.AB AD AC
(1).
0,5
Tam giác ADI đồng dạng tam giác AEC (có góc A chung và
AID ACE
)
Suy ra
AD AI
AE AC
hay
..AI AE AD AC
(2).
0,5
Từ (1) và (2) suy ra
2
.AI AE AB
,
suy ra tam giác ABI đồng dạng tam giác AEB.
Suy ra
2
ABC
AEB ABI
0,5












![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)



