http://ductam_tp.violet.vn/
Ngày thi 21/12/2010
Đ THI KH O SÁT CH T L NG L N 2Ề Ả Ấ ƯỢ Ầ
MÔN: TOÁN
Th i gian làm bàiờ: 180 phút (không k th i gian giao đ )ể ờ ề
I. PH N CHUNG CHO T T C THÍ SINH (7,0 đi m)Ầ Ấ Ả ể
Câu I (2,0 đi mể) Cho hàm s ố
2
m
y x m x
= + + −
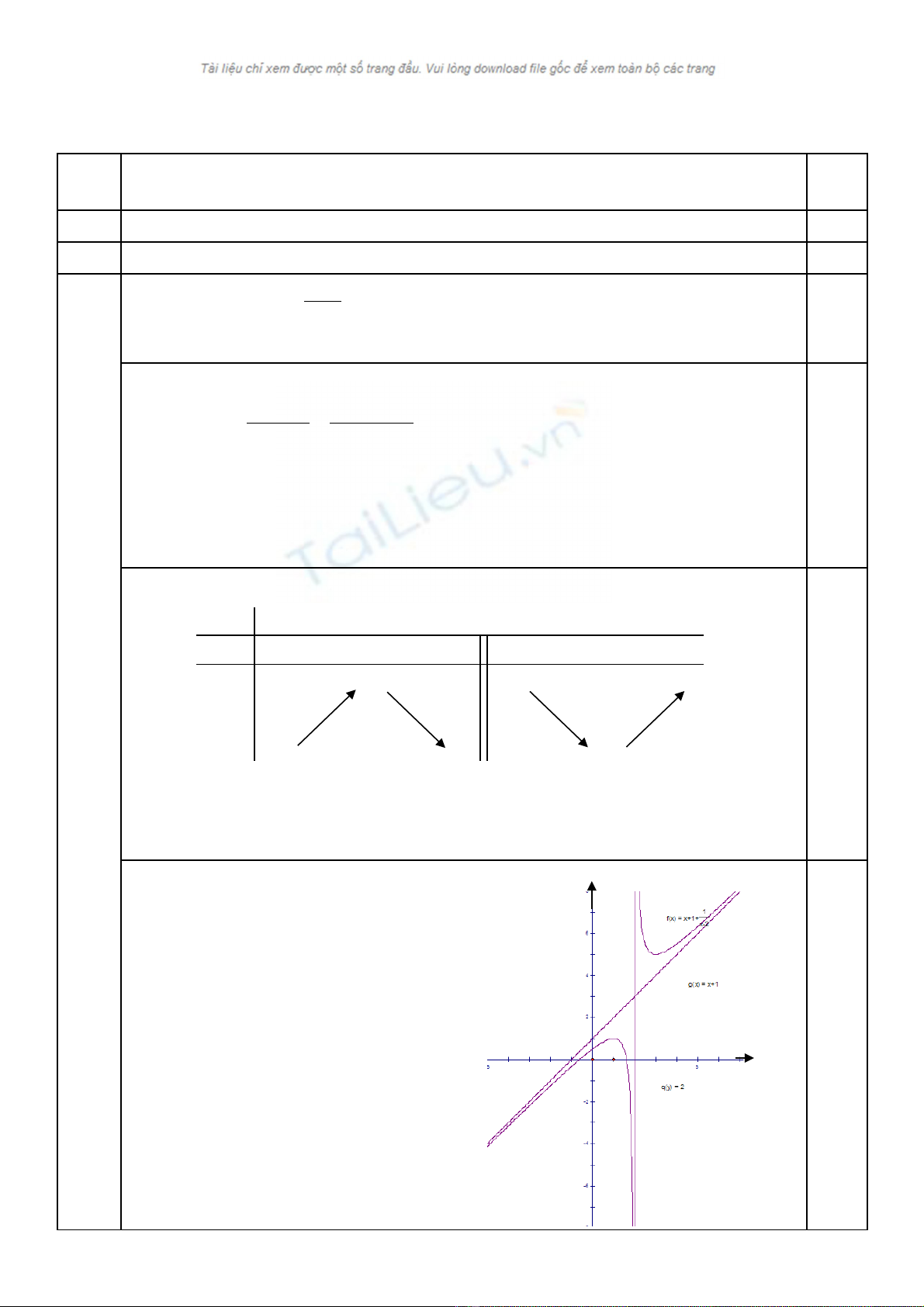
1. Kh o sát s bi n thiên và v đ th hàm s đã cho v i m = 1.ả ự ế ẽ ồ ị ố ớ
2. Tìm m đ hàm s có c c đ i và c c ti u sao cho hai đi m c c tr c a đ th hàm s cách đ ngể ố ự ạ ự ể ể ự ị ủ ồ ị ố ườ
th ng ẳ
d: x – y + 2 = 0 nh ng kho ng b ng nhau.ữ ả ằ
Câu II (2,0 đi m)ể
1. Gi i ph ng trìnhả ươ
( ) ( )
2
cos . cos 1 2 1 sin .
sin cos
x x x
x x
−= +
+
2. Gi iả ph ng trình ươ
2 2
7 5 3 2 ( )x x x x x x− + + = − − ∈¡
Câu III (1,0 đi m). ểTính tích phân
3
0
3
3. 1 3
xdx
x x
−
+ + +
∫
.
Câu IV (1,0 đi mể). Cho t di n đ u ABCD có c nh b ng 1. G i M, N là các đi m l n l t di đ ng trênứ ệ ề ạ ằ ọ ể ầ ượ ộ
các c nh AB, AC sao cho ạ
( ) ( )
DMN ABC⊥
. Đ t AM = x, AN = y. Tính th tích t di n DAMN theo x vàặ ể ứ ệ
y. Ch ng minh r ng: ứ ằ
3 .x y xy+ =
Câu V (1,0 đi mể). Cho x, y, z
0
≥
tho mãn x+y+z > 0. Tìm giá tr nh nh t c a bi u th cả ị ỏ ấ ủ ể ứ
II. PH N RIÊNG (3,0 đi m)Ầ ể : Thí sinh ch đ c làm m t trong hai ph n (ph n A ho c B).ỉ ượ ộ ầ ầ ặ
A. Theo ch ng trình Chu n:ươ ẩ
Câu VI.a (2,0 đi m)ể
1. Trong m t ph ng to đ Oxy, cho hình ch nh t ABCD có ph ng trình đ ng th ng AB: x – 2y + 1 =ặ ẳ ạ ộ ữ ậ ươ ườ ẳ
0, ph ng trình đ ng th ng BD: x – 7y + 14 = 0, đ ng th ng AC đi qua M(2; 1). Tìm to đ các đ nhươ ườ ẳ ườ ẳ ạ ộ ỉ
c a hình ch nh t.ủ ữ ậ
2. Trong không gian to đ Oxyz, cho m t ph ng (P): 2x – y – 5z + 1 = 0 và hai đ ng th ng ạ ộ ặ ẳ ườ ẳ
d1:
1 1 2
2 3 1
x y z+ − −
= =
, d2:
2 2
1 5 2
x y z− +
= = −
Vi t ph ng trình đ ng th ng d vuông góc v i (P) đ ng th i c t hai đ ng th ng dế ươ ườ ẳ ớ ồ ờ ắ ườ ẳ 1 và d2.
Câu VII.a (1,0 đi m).ể Tìm ph n th c c a s ph c z = (1 + i)ầ ự ủ ố ứ n , bi t r ng n ế ằ ∈ N th a mãn ph ng trình ỏ ươ
log4(n – 3) + log4(n + 9) = 3
B. Theo ch ng trình Nâng cao:ươ
Câu VI.b (2,0 đi m)ể
1. Trong m t ph ng to đ Oxy cho tam giác ABC, có đi m A(2; 3), tr ng tâm G(2; 0). Hai đ nh B và Cặ ẳ ạ ộ ể ọ ỉ
l n l t n m trên hai đ ng th ng dầ ượ ằ ườ ẳ 1: x + y + 5 = 0 và d2: x + 2y – 7 = 0. Vi t ph ng trình đ ng trònế ươ ườ
có tâm C và ti p xúc v i đ ng th ng BG. ế ớ ườ ẳ
2. Trong không gian to đ cho đ ng th ng d: ạ ộ ườ ẳ
3 2 1
2 1 1
x y z− + +
= = −
và m t ph ng (P): x + y + z + 2 = 0.ặ ẳ
G i M là giao đi m c a d và (P). Vi t ph ng trình đ ng th ng ọ ể ủ ế ươ ườ ẳ
∆
n m trong m t ph ng (P), vuông gócằ ặ ẳ
v i d đ ng th i tho mãn kho ng cách t M t i ớ ồ ờ ả ả ừ ớ
∆
b ng ằ
42
.
Câu VII.b (1,0 đi m).ể Gi i h ph ng trình ả ệ ươ
( )
1 4
4
2 2
1
log log 1
( , )
25
y x yx y
x y
− − =
∈
+ =
¡
- Đ & đáp án thi Đ i h c - Tr ng THPT Thu n Thành s I ề ạ ọ ườ ậ ố
1
-------------------H t -------------------ế
S L C ĐÁP ÁN VÀ BI U ĐI M Đ THI KH O SÁT L N 2 - 2010Ơ ƯỢ Ể Ể Ề Ả Ầ
Đáp án g m 06 trangồ
Câu N i dungộĐiể
m
I 2,0
1 1,0
V i m =1 thì ớ
1
12
y x x
= + + −
a) T p xác đ nhậ ị : D
{ }
\ 2=¡
0.25
b) S bi n thiên: ự ế
( ) ( )
2
2 2
1 4 3
' 1
2 2
x x
y
x x
− +
= − =
− −
,
1
' 0 3
x
yx
=
= ⇔ =
.
lim
x
y
→−∞
= −∞
,
lim
x
y
→+∞
= +∞
,
2 2
lim ; lim
x x
y y
+ −
→ →
= +∞ = −∞
,
[ ] [ ]
lim ( 1) 0 ; lim ( 1) 0
x x
y x y x
→+∞ →−∞
− + = − + =
Suy ra đ th hàm s có ti m c n đ ng x = 2, ti m c n xiên y = x – 1.ồ ị ố ệ ậ ứ ệ ậ
0.25
B ng bi n thiênả ế
Hàm s đ ng bi n trên m i kho ng ố ồ ế ỗ ả
( ) ( )
;1 , 3; ;−∞ +∞
hàm s ngh ch bi n trênố ị ế
m i kho ng ỗ ả
( ) ( )
1;2 , 2;3
C c tr : Hàm s đ t giá tr c c tr : yự ị ố ạ ị ự ị CĐ = 1 t i x = 1; yạCT = 3 t i x = 3.ạ
0.25
c) Đ thồ ị:
0.25
- Đ & đáp án thi Đ i h c - Tr ng THPT Thu n Thành s I ề ạ ọ ườ ậ ố
2
x
y’
y
-
∞
1 2 3 + ∞
00
+ ∞
+ ∞
-
∞
-
∞
1
3
––
++
2 1.0
V i xớ
≠
2 ta có y’ = 1-
2
( 2)
m
x−
;
Hàm s có c c đ i và c c ti u ố ự ạ ự ể
⇔
ph ng trình (x – 2)ươ 2 – m = 0 (1) có hai nghi mệ
phân bi t khác 2 ệ
0m
⇔ >
0.25
V i m > 0 ph ng trình (1) có hai nghi m là: ớ ươ ệ
1 1
2 2
2 2 2
2 2 2
x m y m m
x m y m m
= + ⇒ = + +
= − ⇒ = + −
0.25
Hai đi m c c tr c a đ th hàm s là A(ể ự ị ủ ồ ị ố
2 ;2 2 )m m m− + −
; B(
2 ; 2 2 )m m m+ + +
Kho ng cách t A và B t i d b ng nhau nên ta có ph ng trình: ả ừ ớ ằ ươ
2 2m m m m− − = − +
0.25
0
2
m
m
=
⇔=
Đ i chi u đi u ki n thì m = 2 tho mãn bài toánố ế ề ệ ả
V y ycbt ậ⇔ m = 2.
0.25
II 2.0
1Gi i ph ng trình ả ươ
( ) ( )
2
cos . cos 1 2 1 sin .
sin cos
x x x
x x
−= +
+
1.0
ĐK:
sin cos 0x x+ ≠
0.25
Khi đó
( )
( ) ( ) ( )
2
1 sin cos 1 2 1 sin sin cosPT x x x x x⇔ − − = + +
( ) ( )
1 sin 1 cos sin sin .cos 0x x x x x⇔ + + + + =
( ) ( ) ( )
1 sin 1 cos 1 sin 0x x x⇔ + + + =
0.25
sin 1
cos 1
x
x
= −
⇔= −
(tho mãn đi u ki n)ả ề ệ 0.25
2
2
2
x k
x m
ππ
π π
= − +
⇔= +
( )
,k m ∈Z
V y ph ng trình đã cho có nghi m là: ậ ươ ệ
2
2
x k
ππ
= − +
và
2x m
π π
= +
( )
,k m ∈Z
0.25
2Gi i ph ng trình: ả ươ
2 2
7 5 3 2 ( )x x x x x x− + + = − − ∈¡
1.0
2
2 2
3 2 0
7 5 3 2
x x
PT
x x x x x
− − ≥
⇔− + + = − −
0.25
2
3 2 0
5 2( 2)
x x
x x x
− − ≥
⇔+ = − +
0.25
- Đ & đáp án thi Đ i h c - Tr ng THPT Thu n Thành s I ề ạ ọ ườ ậ ố
3
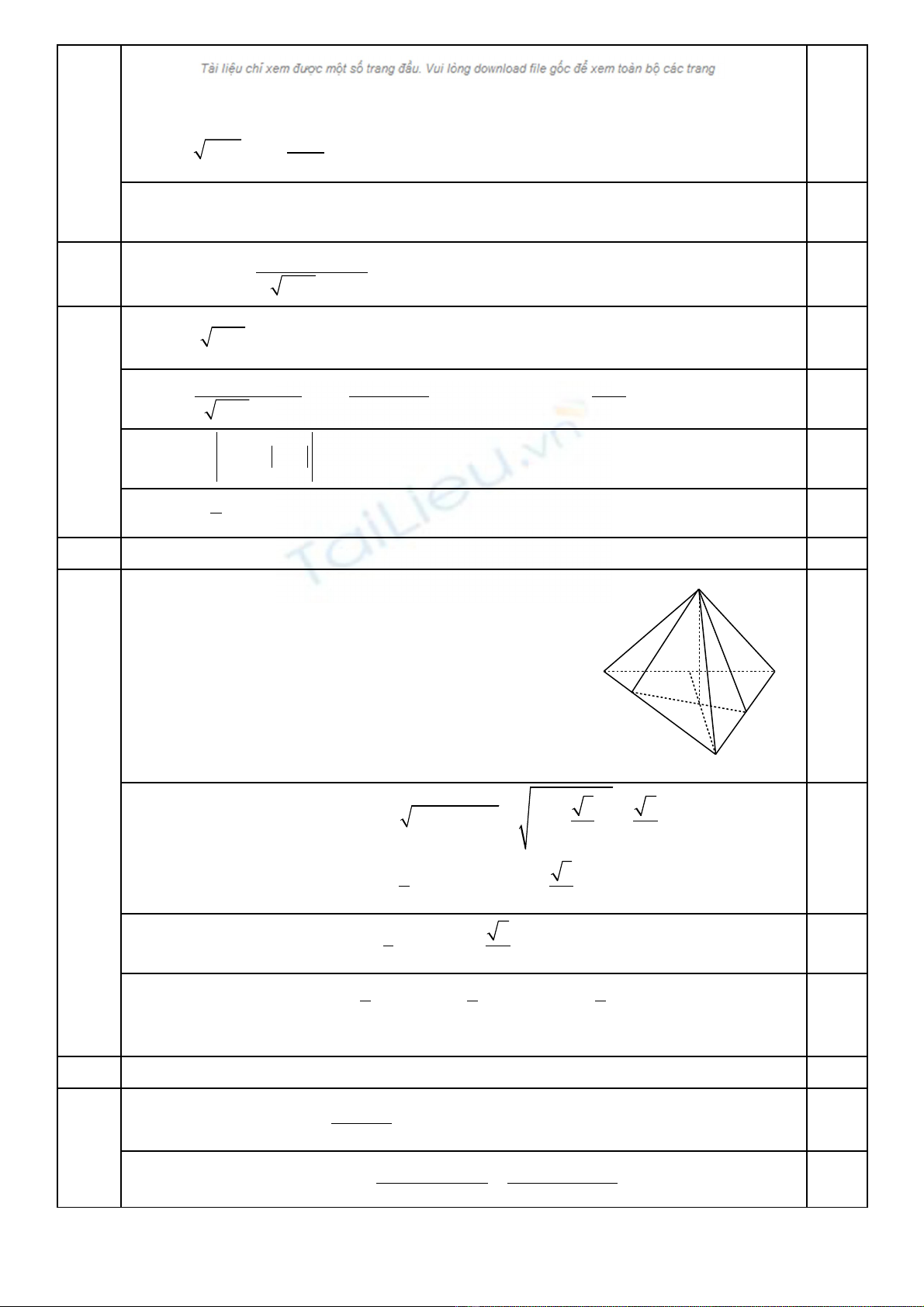
3 1
0
2
5 2.
x
x
x
xx
− ≤ ≤
⇔ ≠
+
+ = −
( )
( )
2
2 0
1 16 0
x
x x
− ≤ <
⇔+ − =
0.25
1x⇔ = −
V y ph ng trình đã cho có m t nghi m x = - 1. ậ ươ ộ ệ 0.25
III Tính tích phân
3
0
3
3. 1 3
xdx
x x
−
+ + +
∫
.1.0
Đ t u = ặ
2
1 1 2x u x udu dx+ ⇒ − = ⇒ =
; đ i c n:ổ ậ
0 1
3 2
x u
x u
= ⇒ =
= ⇒ =
0.25
Ta có:
3 2 2 2
3
2
0 1 1 1
3 2 8 1
(2 6) 6
3 2 1
3 1 3
x u u
dx du u du du
u u u
x x
− −
= = − +
+ + +
+ + +
∫ ∫ ∫ ∫
0.25
( )
2
2
1
2
6 6 ln 1 1
u u u= − + +
0.25
3
3 6ln 2
= − +
0.25
IV 1.0
D ng ự
DH MN H
⊥ =
Do
( ) ( ) ( )
DMN ABC DH ABC⊥ ⇒ ⊥
mà
.D ABC
là
t di n đ u nên ứ ệ ề
H
là tâm tam giác đ u ề
ABC
.
0.25
Trong tam giác vuông DHA:
2
2 2 2
3 6
13 3
DH DA AH
= − = − =
÷
÷
Di n tích tam giácệ
AMN
là
0
1 3
. .sin 60
2 4
AMN
S AM AN xy= =
0.25
Th tích t di n ể ứ ệ
.D AMN
là
1 2
.
3 12
AMN
V S DH xy= =
0.25
Ta có:
AMN AMH AMH
S S S= +
0 0 0
1 1 1
.sin 60 . .sin 30 . .sin 30
2 2 2
xy x AH y AH⇔ = +
⇔
3 .x y xy+ =
0.25
V 1.0
Tr c h t ta có: ướ ế
( )
3
3 3
4
x y
x y +
+ ≥
(bi n đ i t ng đ ng) ế ổ ươ ươ
( ) ( )
2
... 0x y x y⇔ ⇔ − + ≥
0.25
Đ t x + y + z = a. Khi đó ặ
( ) ( ) ( )
3 3
3 3
33
3 3
64 64
4 1 64
x y z a z z
P t t
a a
+ + − +
≥ = = − +
0.25
- Đ & đáp án thi Đ i h c - Tr ng THPT Thu n Thành s I ề ạ ọ ườ ậ ố
4
D
A
B
C
H
M
N
(v i t = ớ
z
a
,
0 1t≤ ≤
)
Xét hàm s f(t) = (1 – t)ố3 + 64t3 v i tớ
[ ]
0;1∈
. Có
( )
[ ]
2
2
1
'( ) 3 64 1 , '( ) 0 0;1
9
f t t t f t t
= − − = ⇔ = ∈
L p b ng bi n thiênậ ả ế
0.25
( )
[ ]
0;1
64
inf 81
t
M t
∈
⇒ = ⇒
GTNN c a P là ủ
16
81
đ t đ c khi x = y = 4z > 0ạ ượ 0.25
VI.a 2.0
1 1.0
Do B là giao c a AB và BD nên to đ c a B là nghi m c a h :ủ ạ ộ ủ ệ ủ ệ
21
2 1 0 21 13
5;
7 14 0 13 5 5
5
x
x y B
x y y
=
− + =
⇔ ⇒
÷
− + =
=
0.25
L i có: T giác ABCD là hình ch nh t nên góc gi a AC và AB b ng góc gi a AB vàạ ứ ữ ậ ữ ằ ữ
BD, kí hi u ệ
(1; 2); (1; 7); ( ; )
AB BD AC
n n n a b− −
uuur uuur uuur
(v i aớ2+ b2 > 0) l n l t là VTPT c a cácầ ượ ủ
đ ng th ng AB, BD, AC. Khi đó ta có: ườ ẳ
( ) ( )
os , os ,
AB BD AC AB
c n n c n n=
uuur uuur uuur uuur
2 2 2 2
3
2 7 8 0
27
a b
a b a b a ab b b
a
= −
⇔ − = + ⇔ + + = ⇔ = −
0.25
- V i a = - b. Ch n a = 1 ớ ọ
⇒
b = - 1. Khi đó Ph ng trình AC: x – y – 1 = 0, ươ
A = AB ∩ AC nên to đ đi m A là nghi m c a h :ạ ộ ể ệ ủ ệ
1 0 3 (3; 2)
2 1 0 2
x y x A
x y y
− − = =
⇒ ⇒
− + = =
G i I là tâm hình ch nh t thì I = AC ọ ữ ậ ∩ BD nên to đ I là nghi m c a h :ạ ộ ệ ủ ệ
7
1 0 7 5
2;
7 14 0 5 2 2
2
x
x y I
x y y
=
− − =
⇔ ⇒
÷
− + =
=
Do I là trung đi m c a AC và BD nên to đ ể ủ ạ ộ
( )
14 12
4;3 ; ;
5 5
C D
÷
0.25
- V i b = - 7a (lo i vì AC không c t BD)ớ ạ ắ 0.25
2 1.0
Ph ng trình tham s c a dươ ố ủ 1 và d2 là:
1 2
1 2 2
: 1 3 ; : 2 5
2 2
x t x m
d y t d y m
z t z m
= − + = +
= + = − +
= + = −
0.25
Gi s d c t dả ử ắ 1 t i M(-1 + 2t ; 1 + 3t ; 2 + t) và c t dạ ắ 2 t i N(2 + m ; - 2 + 5m ; - 2m) ạ
MN⇒uuuur
(3 + m - 2t ; - 3 + 5m - 3t ; - 2 - 2m - t).
0.25
- Đ & đáp án thi Đ i h c - Tr ng THPT Thu n Thành s I ề ạ ọ ườ ậ ố
5