PHÒNG GIÁO D C- ĐÀO T OỤ Ạ
HUY N TR C NINHỆ Ự
Đ ki m tra có 01 trangề ể
Đ KI M TRA CH T LỀ Ể Ấ NG H C KỲ IIƯỢ Ọ
NĂM H C 2009-2010Ọ
Môn Toán l p 9ớ
Th i gian 90 phút ( Không k th i gian giao đ )ờ ể ờ ề
I. Tr c nghi m:ắ ệ (1,5 đi m). Các câu d i đây, m i câu có nêu 4 ph ng án (A, B, C, D),ể ướ ỗ ươ
trong đó ch có m t ph ng án đúng. Hãy ch n ph ng án đúng (ch c n vi t tên ch cái đ ngỉ ộ ươ ọ ươ ỉ ầ ế ữ ứ
tr c ph ng án vào bài làm)ướ ươ .
Câu 1 : Ph ng trình xươ 2 + x - 2 = 0 có nghi m là:ệ
A. x1 = 1; x2 = 2. B. x1 = 1; x2 = -2. C. x1 = -1; x2 = 2. D. x1 = -1; x2 = -2.
Câu 2: Bi t đi m A (2; m + 6) thu c đ th hàm s y = 2xế ể ộ ồ ị ố 2. Khi đó m b ng:ằ
A. 8 B. 4 C. 2 D. -2
Câu 3: Di n tích m t c u có đ ng kính 5cm làệ ặ ầ ườ
A. 25
π
cm2B. 50
π
cm2C. 100
π
cm2D. 150
π
cm2
Câu 4: N u di n tích hình tròn là 2ế ệ
π
thì chu vi đ ng tròn đó là:ườ
A.
π
B. 2
2
π
C. 3
π
D. 4
π
Câu 5: Bán kính c a đ ng tròn ngo i ti p tam giác đ u có c nh b ng 3 là:ủ ườ ạ ế ề ạ ằ
A. 3 B.
1
3
C.
2
3
D.
3
Câu 6: N u a.c < 0 thì s nghi m c a ph ng trình axế ố ệ ủ ươ 4 + bx2 + c = 0 là:
A. 4 B. 3 C. 2 D. vô nghi mệ
II. T lu n:ự ậ (8,5 đi m)ể
Câu 1: (2 đi m). ểCho bi u th c: ể ứ
+ −
+ +
÷ ÷
÷ ÷
+ −
x x x x
A = 1 1
x 1 x 1
;
≥
≠
Ví i x 0,
x 1.
a. Rút g n bi u th c A.ọ ể ứ
b. Tìm giá tr c a bi u th c A bi t x = ị ủ ể ứ ế
Câu 2: (1 đi m). ểGi i h ph ng trình sau: ả ệ ươ
( ) ( )
( ) ( )
x +3 y-1 = xy +2
x -1 y +3 = xy -2
Câu 3: (1,75 đi m). ểCho ph ng trình: xươ 2 - 2(m - 1)x + m2 + m – 2 = 0
a. Gi i ph ng trình v i m = -2ả ươ ớ
b. Xác đ nh m đ ph ng trình đã cho có 2 nghi m phân bi t th a mãn:ị ể ươ ệ ệ ỏ
+ =
2 2
1 2
x x 8
.
Câu 4: (3 đi m). ểT đi m A bên ngoài đ ng tròn (O) k hai ti p tuy n AB và ACừ ể ở ườ ẻ ế ế
(B, C là các ti p đi m). M là đi m b t kì trên cung nh BC. K MI ế ể ể ấ ỏ ẻ
⊥
AB, MH
⊥
BC,
MK
⊥
AC (I , H , K là chân các đ ng vuông góc)ườ
a. Ch ng minh t giác BIMH n i ti p.ứ ứ ộ ế
b. Ch ng minh MH ứ2 = MI.MK
c. G i P là giao đi m c a IH và MB. Q là giao đi m c a KH và MC.ọ ể ủ ể ủ
Ch ng minh t giác MPHQ n i ti p.ứ ứ ộ ế
Câu 5: (0,75 đi m). ểTìm giá tr nh nh t c a bi u th c:ị ỏ ấ ủ ể ứ
P =
÷ ÷
a b
x + x +
x x
; v i x > 0, a và b là các h ng s d ng cho tr c.ớ ằ ố ươ ướ
-------------------- H t --------------------ế
Đ CHÍNH TH CỀ Ứ
PHÒNG GIÁO D C VÀ ĐÀO T OỤ Ạ H NG D N CH MƯỚ Ẫ Ấ
HUY N TR C NINHỆ Ự KI M TRA CH T L NG H C KỲ II Ể Ấ ƯỢ Ọ
TOÁN L P 9Ớ
I. Tr c nghi m: 1,5 đi m. M i câu đúng cho 0,25 đi mắ ệ ể ỗ ể
Câu Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6
Đáp án B C A B D C
II. T lu n: 8,5 đi mự ậ ể
Câu Ý N i dungộĐi mể
Câu 1
2 đ
a.
1 đ
b.
1 đ
V i ớ
≥ ≠x 0, x 1
thì bi u th c:ể ứ
( ) ( )
( ) ( )
+ −
+ +
+ −
+ −
= + +
+ −
= + −
= −
÷ ÷
x x x x
P = 1 1
x 1 x 1
x 1 x x 1 x
1 1
x 1 x 1
1 x 1 x
1 x
V iớ x =
( )
2
1 1 13 3 3= − = − = −
Thì bi u th c P = ể ứ
( )
1 1 1 3 1 2 33− − = − + = −
0,25
0,25
0,25
0,25
0,5
0,5
Câu 2
1 đ
( ) ( )
( ) ( )
⇔
⇔
x +3 y-1 = xy +2
x -1 y +3 = xy -2
xy - x +3y -3= xy +2
xy +3x - y -3= xy -2
-x +3y = 5
3x - y =1
HS tìm đúng x = 1
HS tìm đúng y = 2
V y h ph ng trình đã cho có nghi m là ậ ệ ươ ệ
x =1
y = 2
0,25
0,25
0,25
0,25
Câu 3
1,75đ
a.
0,75đ
V i m = -2 thì ph ng trình đã cho tr thành:ớ ươ ở
x2 - 2(-2 - 1)x + (-2)2 - 2 - 2 = 0
⇔
x2 + 6x = 0
⇔
x(x + 6) = 0
⇔
x = 0
x = -6
0,25
0,25
0,25
b.
1 đ
x2 - 2(m - 1)x + m2 + m – 2 = 0
HS tìm đ c ượ
∆
’ = -3m + 3
Đi u ki n đ ph ng trình có 2 nghi m phân bi t là ề ệ ể ươ ệ ệ
∆
’ > 0
Suy ra m < 1
0,25
Vì x1, x2 là nghi m c a ph ng trình đã cho nên theo h th cệ ủ ươ ệ ứ
Vi-et ta có: x1 + x2 = 2(m - 1) và x1.x2 = m2 + m - 2.
Theo bài ra:
+ =
2 2
1 2
x x 8
⇔
(x1 + x2)2 - 2x1.x2 = 8
Suy ra [2(m - 1)]2 – 2(m2 + m - 2) = 8
Suy ra 2m2 - 10m = 0
Gi i ph ng trình tìm đ c m = 0 và m = 5ả ươ ượ
Đ i chi u v i đi u ki n m < 1 ta th y m = 5 không th aố ế ớ ề ệ ấ ỏ
mãn.
V y m = 0 ph ng trình đã cho có 2 nghi m phân bi t th aậ ươ ệ ệ ỏ
mãn:
+ =
2 2
1 2
x x 8
.
0,25
0,25
0,25
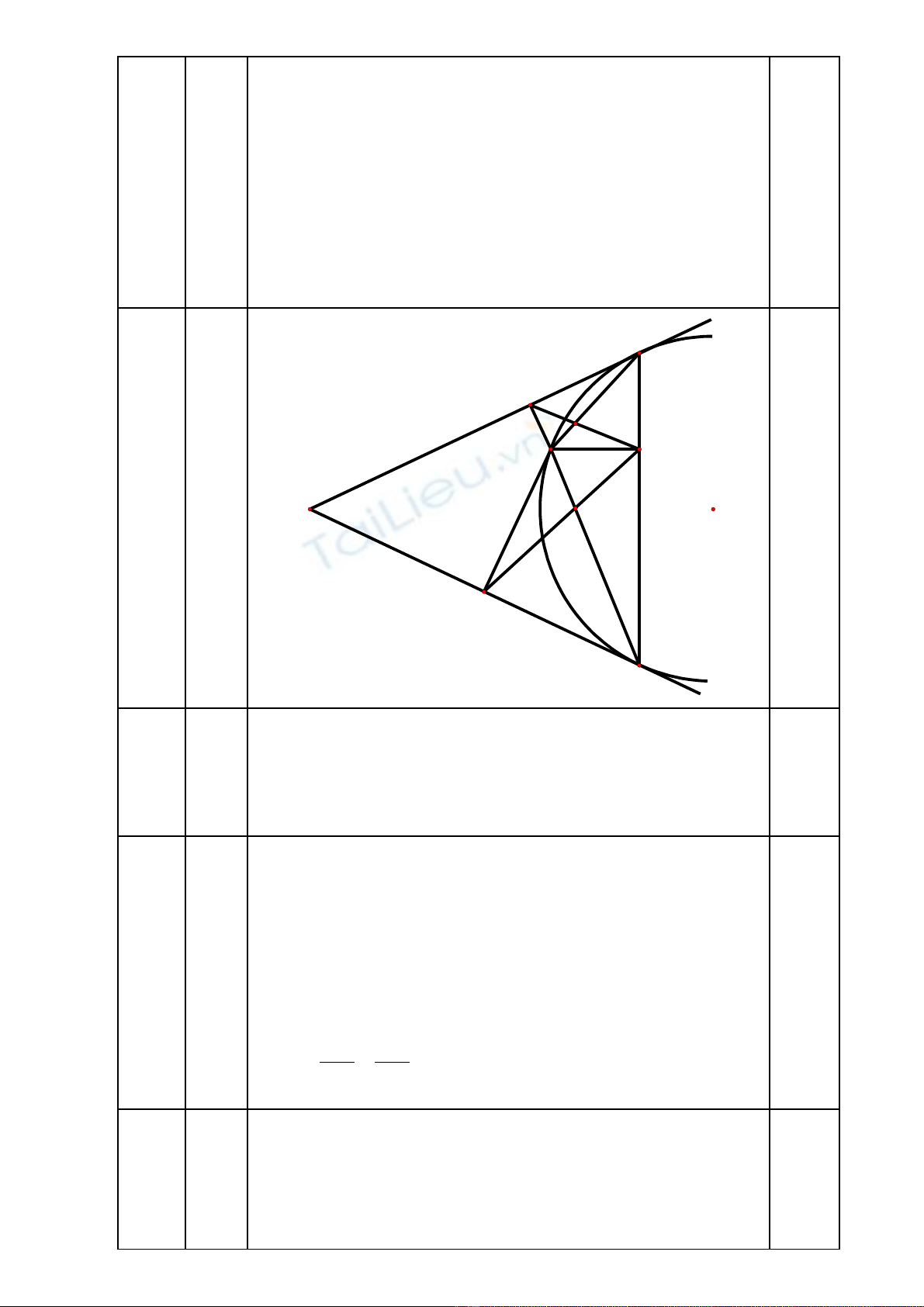
Câu 4
3 đ
Q
P
K
H
I
C
B
A
M
a.
1 đ
Vì MI
⊥
AB (gt)
⇒
·
BIM
= 90O
Vì MH
⊥
BC (gt)
⇒
·
BHM
= 90O
Ta có
·
BIM
+
·
BHM
= 90O + 90O = 180O
Suy ra t giác BIMH n i ti p (T giác có t ng hai góc đ iứ ộ ế ứ ổ ố
di n b ng 180ệ ằ O)
0,25
0,25
0,25
0,25
b.
1 đ Vì t giác BIMH n i ti p (cmt). Suy ra ứ ộ ế
·
MIH
=
·
MBH
(1)
Trong đ ng tròn (O) có ườ
·
MBH
=
·
MCK
(Góc t o b i tia ti pạ ở ế
tuy n và dây cung b ng góc n i ti p cùng ch n m t cung) (2)ế ằ ộ ế ắ ộ
Ch ng minh t ng t câu a ta có t giác CKMH n i ti p. Suyứ ươ ự ứ ộ ế
ra
·
MCK
=
·
MHK
(3)
T (1), (2) và (3). Suy ra: ừ
·
MIH
=
·
MHK
(4)
Ch ng minh t ng t ta có: ứ ươ ự
·
MKH
=
·
MHI
(5)
T (4) và (5) suy ra ừ
∆
MIH đ ng d ng ồ ạ
∆
MHK (g.g)
Suy ra:
MH MI
=
MK MH
hay MH2 = MI.MK (đpcm)
0,25
0,25
0,25
0,25
c.
1 đ Ch ng minh: ứ
·
MHK
=
·
MCK
=
·
MBC
Ch ng minh: ứ
·
IHM
=
·
IBM
=
·
MCB
Suy ra
·
MHK
+
·
IHM
=
·
MBC
+
·
MCB
Suy ra
·
BMC
+
·
MHK
+
·
IHM
=
·
BMC
+
·
MBC
+
·
MCB
= 180O(t ng 3 góc trong ổ
∆
MBC)
0,25
0,25
0,25
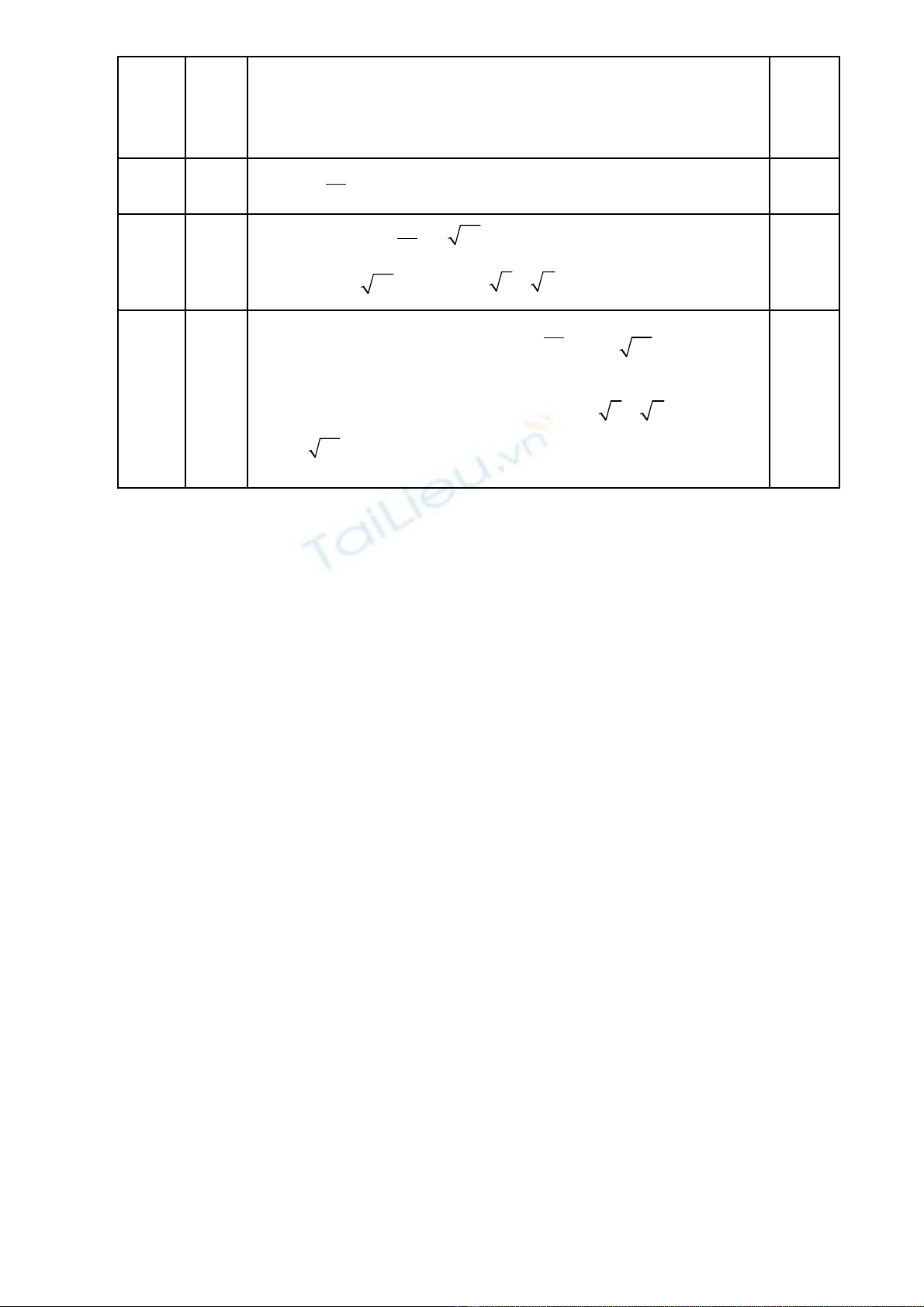
Hay
·
PMQ
+
·
PHQ
= 180O
Suy ra t giác MPHQ n i ti p (T giác có t ng hai góc đ iứ ộ ế ứ ổ ố
di n b ng 180ệ ằ O)
0,25
Câu 5
0,75đ.
÷
ab
P= x + +a+ b
x
0,25
Ch ng minh: ứ
≥
ab
x + 2 ab
x
Suy ra P
≥
2 ab
+ a + b =
( )
2
a + b
0,25
D u “=” x y ra khi và ch khi ấ ả ỉ
⇔
ab
x = x = ab
x
x > 0
V y giá tr nh nh t c a bi u th c P là: ậ ị ỏ ấ ủ ể ứ
( )
2
a + b
⇔x = ab
0,25
Chú ý: + Trên đây các bài toán ch là h ng d n ch m m t cách gi i. N u h c sinh gi iỉ ướ ẫ ấ ở ộ ả ế ọ ả
cách khác l p lu n lô gích, đúng thì cho đi m t ng đ ng.ậ ậ ể ươ ươ
+ Bài hình không ch m n u không v hình ho c hình v saiấ ế ẽ ặ ẽ