S GD VÀ ĐT H I D NGỞ Ả ƯƠ
TR NG THPT ĐOÀNƯỜ
TH NGƯỢ
Đ CHÍNH TH CỀ Ứ
Đ THI ỀKH O SÁT CH T L NG L N Ả Ấ ƯỢ Ầ 1
NĂM H C 2021 - 2022Ọ
MÔN THI: TOÁN 10
Th i gian làm bài: 120 phút, không k th i gian phát đờ ể ờ ề
Câu 1 (1,5 đi mể)
a) Cho hai t p h p ậ ợ
{ }
1;3;4;5;6;7A
=
và
{ }
0;2;4;6;8B
=
. Tìm t p h p ậ ợ
\C A B
=
?
b) Cho
A
,
B
,
C
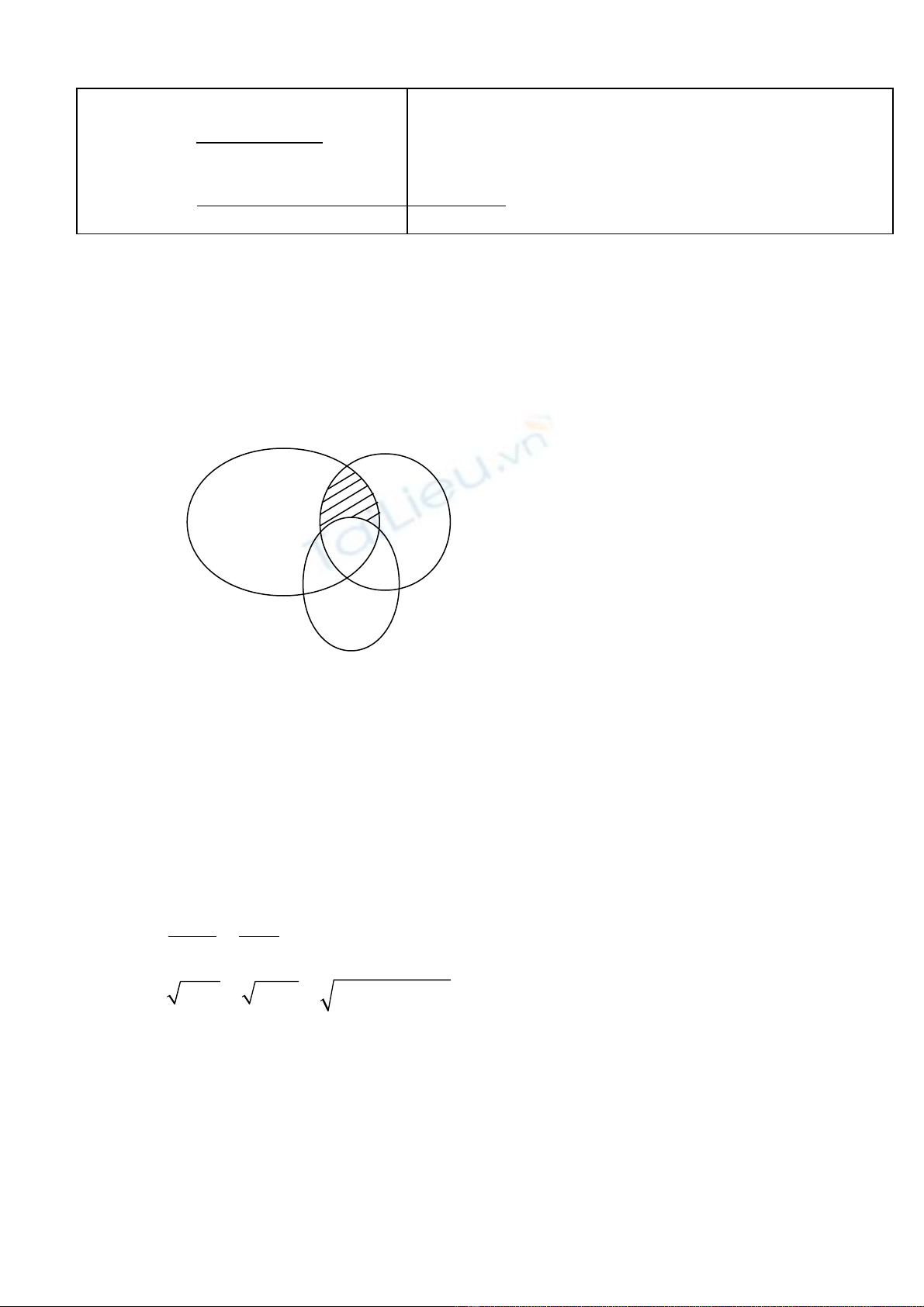
là các t p h p b t kì, có bi u đ Ven mô t nh hình v d iậ ợ ấ ể ồ ả ư ẽ ướ
đây. Tìm t p h p mô t ph n g ch s c trong bi u đ Ven trên?ậ ợ ả ầ ạ ọ ể ồ
Câu 2 (1,5 đi mể). Cho hàm s ố
( )
2 2
2 1 1y x mx m m= − + − +
.
a) L p b ng bi n thiên c a hàm s khi ậ ả ế ủ ố
2m
=
.
b) Tìm các giá tr c aị ủ m đ đ th hàm s ể ồ ị ố
( )
1
c t tr c hoành t i hai đi m có hoànhắ ụ ạ ể
đ ộ
sao cho t ng ổ
2 2
1 2
S x x
= +
đt giá tr nh nh t.ạ ị ỏ ấ
Câu 3 (2,5 đi mể). Gi i các ph ng trình sau:ả ươ
a)
( ) ( )
2
4 2 3 2x x x− = + −
.
b)
2
5 3
1 1
x
x x
−=
− +
.
c)
( ) ( )
1 4 1 4 5x x x x
+ + − + + − =
Câu 4 (0,5 đi mể). Gi i h ph ng trình:ả ệ ươ
( )
( )
2
4 2 2
3 3 0
9 5 0
x xy x y
x y x y x
+ − − =
+ + − =
Câu 5 (0,5 đi mể). Cho 4 đi m b t k ể ấ ỳ
, , ,A B C O
. Đng th c nào sau đây là đúng?ẳ ứ
A.
.OA OB BA
= −
uuur uuur uuur
B.
.AB AC BC
= +
uuur uuur uuur
C.
.AB OB OA
= +
uuur uuur uuur
D.
.OA CA CO
= −
uuur uuur uuur
AB
C
Câu 6 (0,5 đi mể). Cho đo n th ng ạ ẳ
AB
có đ dài b ng ộ ằ
.a
M t đi m ộ ể
M
di đng saoộ
cho
MA MB MA MB
+ = −
uuur uuur uuur uuur
. G i ọ
H
là hình chi u c a ế ủ
M
lên
AB
. Tính đ dài l n nh tộ ớ ấ
c a ủ
MH
?
Câu 7 (1,0 đi mể). Trong m t ph ng to đ ặ ẳ ạ ộ
Oxy
, cho hai đi m ể
( )
2;4A
và
( )
1;2B
. Tính
đ dài véc t ộ ơ
.AB
uuur
Câu 8 (0,5 đi mể). Cho hình ch nh t ữ ậ
ABCD
có
3AB
=
,
4AD
=
. G i ọ
M
là đi mể
tho mãn đi u ki n ả ề ệ
.AM k AB
=
uuuur uuur
. Xác đnh ị
k
đ hai đng th ng ể ườ ẳ
AC
và
DM
vuông
góc nhau?
Câu 9 (0,5 đi mể). Rút g n bi u th c:ọ ể ứ
2 2 0 0 2 2 0
4
4 sin 30 2 cos180 sin 60 .
3
P a ab b= − +
V iớ
,a bﾡ
.
Câu 10 (0,5 đi mể). Cho
cot 2
α
=
. Tính giá tr bi u th c: ị ể ứ
sin 2cos
sin cos
Q
α α
α α
−
=+
.
Câu 11 (0,5 đi mể). Cho ph ng trình: ươ
4 3 2
4 6 2 0x x x x m
− + + + + =
(
m
là tham s ).ố
Tìm t t c các giá tr ấ ả ị
m
đ ph ng trình trên có 3 nghi m phân bi t.ể ươ ệ ệ
---------------------------------H t---------------------------------ế
H và tên : ………………………..…………………….; S báo d nh : ………….ọ ố ạ
H NG D N CH M ĐI MƯỚ Ẫ Ấ Ể
Câu N i dungộĐiể
m
1a
1,0 đi mểT p ậ
{ }
1;3;5;7C=
. 1,0
1b
0,5 đi mểLà t p h p ậ ợ
( )
\A B C
0,5
2a
1,0 đi mể
Khi
2m
=
ta có
2
4 3y x x= − +
. T p xác đnh ậ ị
D R=
T a đ đnh :ọ ộ ỉ
(2; 1)I−
0,25
Hàm s ngh ch bi n trên ố ị ế
( )
; 2−
và đng bi n trên ồ ế
( )
2;+
0,25
V b ng bi n thiên : ẽ ả ế
x
−
2
+
y
+
+
1−
0,5
2b
0,5 đi mể
Ph ng trình hoành đ giao đi m ươ ộ ể
( )
2 2
2 1 0 1x mx m m− + − + =
Đ đ th hàm s c t ể ồ ị ố ắ Ox t i 2 đi m thì ạ ể
' 1 0 1m m∆= −�۳
Theo Viet:
1 2
2
1 2
2
. 1
x x m
x x m m
+ =
= − +
( )
2
2 2 2
1 2 1 2 1 2
2 2 2 2S x x x x x x m m
= + = + − = + −
0,25
L p BBT c a hs ậ ủ
( )
2
2 2 2f m m m= + −
trên
[
)
1;
+
Tìm đc GTNN c a ượ ủ
S
b ng 2 đt đc t i ằ ạ ượ ạ
1m=
.0,25
3a
1,0 đi mể
( ) ( ) ( ) ( ) ( ) ( )
2
4 2 3 2 2 2 2 3 2x x x x x x x− = + − − + = + −�
0,5
( ) ( )
2
2 1 0 1
x
x x x
=
− + = = −
0,5
3b
1,0 đi mểĐK:
1x
0,25
PT
( )
5 3 1x x
− = −�
0,25
2 2 1x x
= − = −� �
0,25
K t h p đk suy ra pt vô nghi mế ợ ệ 0,25
3c
0,5 đi mể ĐK:
1 4x−
Đt ặ
1 4 ; 0t x x t
= + + −
( ) ( )
25
1 4 2
t
x x −
+ − =�
0,25
PT tr thành:ở
22
55 2 15 0
2
t
t t t
−
+ = + − =�
( )
( )
3
5
t tm
t L
=
= −
( ) ( ) ( )
2
0
3 1 4 2 3 0 3
x
t x x x x tm
x
=
= + − = − =� � � =
0,25
4
0,5 đi mể
( )
( )
( )
( )
( )
2
2
2
4 2 2 2 2 2
3 3 3 1
3 3 0
9 5 0 3 5 3 2
x y x xy
x xy x y
x y x y x x y x x y
+ = −
+ − − =
� �
� �
+ + − = + − +
� �
Th (1) vào (2) ta đc: ế ượ
( )
2 2
9 15 4 0x y y− + =
0,25
0
1
3
4
3
x
y
y
=
=�=
0 0x y= =�
11
3
y x= =�
( )
2
44 0
3
y x x VN= + + =�
KL: H pt có 2 nghi m: ệ ệ
( )
1
0;0 , 1;3
� �
� �
� �
� �
� �
�
0,25
5
0,5 đi mểD.
.OA CA CO
= −
uuur uuur uuur
0,5
6
0,5 đi mểG i ọ
O
là trung đi m ể
AB
. Khi đó
2MA MB MO
+ =
uuur uuur uuuur
.
Ta có
2MA MB MA MB MO BA
+ = − =�
uuur uuur uuur uuur uuuur uuur
hay
MO AB
=
.
Suy ra
MO OA OB
= =
Do đó
M
n m trên đng tròn tâm ằ ườ
O
đng kính ườ
AB
.
0,25
MH
l n nh t khi ớ ấ
H
trùng v i tâm ớ
O
hay
max .
2 2
AB a
MH MO
= = =
0,25
7
1,0 đi mể
( ) ( ) ( )
2 2
1; 2 1 2 5AB AB
= − − = − + − =�
uuur
1,0
8
0,5 đi mểTa có:
( ) ( )
. . . . . .
16 9
AC DM BC BA AM AD BC AM BC AD BA AM BA AD
k
= − − = − − +
= − +
uuur uuuur uuur uuur uuuur uuur uuur uuuur uuur uuur uuur uuuur uuur uuur
. 0,25
Khi đó
16
. 0 9
AC DM AC DM k
⊥ = =� �
uuur uuuur
.0,25
Cách 2: Ch n h t a đ ọ ệ ọ ộ Oxy sao cho A là g c t a đ, canh ố ọ ộ AB n mằ
trên tr c tung, ụAD n m trên tr c hoành (theo chi u d ng), khi đóằ ụ ề ươ
( ) ( ) ( ) ( )
0;0 , 0;3 , 4;0 , 4;3A B D C
. Gi s ả ử
( )
;M x y
( )
. 0;3AM k AB M k
=
uuuur uuur
0,25
( ) ( )
4;3 , 4;3AC DM k−
uuur uuuur
16
. 0 9 16 0 9
AC DM AC DM k k⊥ = − = = −� � �
uuur uuuur
0,25
9
0,5 đi mể
( )
2
2
2 2
1 4 3
4 2 1
2 3 2
P a ab b � �
� �
= − − + � �
� �
� � � �
0,25
( )
2
2 2
2P a ab b a b= + + = +
0,25
10
0,5 đi mểDo
cot 2 sin 0
α α
=
. Chia c t s và m u s cho ả ử ố ẫ ố
sin
α
ta
đc ượ
1 2cot
1 cot
Q
α
α
−
=+
0,25
( ) ( )
1 2 2 1 2 2 2 1 3 2 5
1 2
Q−
= = − − = −
+
0,25
11
0,5 đi mểPt
( ) ( )
( )
2
2 2
2 3 2 2 0 1x x x x m
− − − + + =�
Đt ặ
2
2t x x= −
. Đk c a ủ
t
đ t n t i ể ồ ạ x là
1t
−
(1) tr thành: ở
( )
2
3 2 0 2t t m
− + + =
V i ớ
1t
= −
cho m t giá tr ộ ị
x
.
V i m i ớ ỗ
1t
> −
cho hai giá tr ị
x
0,25
(1) có ba nghi m phân bi t ệ ệ
( )
2
có hai nghi m ệ
1 2
,t t
t/m
1
2
1
1
t
t
= −
> −
g/s (2) có nghi m ệ
1 6t m= − = −�
.
Th lai: v i ử ớ
6m= −
ph ng trình (2) có hai nghi m ươ ệ
1 2
1; 4t t
= − =
(tm ycbt)
KL:
6m
= −
0,25