
UBND HUYỆN BÌNH XUYÊN
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KSCL MÔN TOÁN 9 – LẦN 1_T11.2024
Năm học: 2024 - 2025
Thời gian: 120 phút (Không kể thời gian giao đề)
I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)
Thí sinh trả lời từ câu 1 đến câu 8. Mỗi câu hỏi thí sinh chỉ chọn một phương án (Ví dụ: Câu
1 chọn A, ghi 1.A)
Câu 1. Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
A. 2
3 5 0
x y
. B. 3
5
y
x
. C.
1
xy x
. D.
4
2 3
x y
Câu 2. Hệ phương trình
4x 3y 5
3x y 7
có nghiệm là:
A.
2;1
. B.
2;1
. C.
2; 1
. D.
2; 1
.
Câu 3. Biết rằng
m n
với
m
,
n
bất kỳ, chọn câu đúng.
A.
1 1
n m
. B.
5 5
m n
.
C.
4 4
m n
. D.
2 2
n m
.
Câu 4. Giá trị
5
x
là một nghiệm của bất phương trình nào sau đây:
A.
6 2 0
x
. B.
4 8 0
x
. C.
2 8 0
x
. D.
2 3 0
x
.
Câu 5. Cho tam giác
ABC
có
o
90 , , , ,
A AB c AC b BC a
ta có:
A. sin
b
B
c
. B. sin
b
B
a
. C. sin
b
C
a
. D. sin
b
C
c
.
Câu 6. Biết
4
cos
5
, tính
bằng cách sử dụng máy tính cầm tay:
A.
36 87'.
B.
36 9'.
C.
36 53'.
D.
36 52 '.
Câu 7. Cho tam giác
MNP
vuông tại
M
. Hệ thức nào sau đây là đúng?
A.
.sin
MP NP P
. B.
.cot
MP MN P
. C.
.tan
NP MN P
. D.
.cos
NP MP P
.
Câu 8. Cho tam giác
MNP
có
o o
90 , 70 , 15
M P MN cm
. Khi đó độ dài cạnh
NP
bằng:
A.
14
cm
. B.
44
cm
. C.
16
cm
. D.
5
cm
.
II. TỰ LUẬN (8,0 điểm)
Câu 9. (1,0 điểm). Tìm hệ số
,
x y
trong phản ứng hóa học đã được cân bằng sau:
3 2
xFeCl Fe yFeCl
Câu 10 (1,5 điểm). Giải hệ phương trình, phương trình sau:
a)
2 3 1
3 2 9
x y
x y b)
5 2 5 0
x x x
c)
2
1 1 8
1 1
1
x x
x x x
Câu 11 (0,5 điểm). Cho
,
a b
chứng minh rằng:
3 2 3 2 .
a b
Câu 12 (1,0 điểm). Giải bài toán bằng cách lập hệ phương trình:
Một chiếc bếp từ và một chiếc nồi chiên không dầu được niêm yết với giá tổng cộng là
21
triệu đồng. Nhân dịp sắp đến Tết Dương lịch năm 2025, cửa hàng giảm giá
15%
cho mỗi cái
bếp từ và
10%
với mỗi cái nồi chiên không dầu so với giá niêm yết, do đó bác An đi mua hai
sản phẩm này chỉ hết
18,3
triệu đồng. Tính giá niêm yết của một chiếc bếp từ và một chiếc
nồi chiên không dầu?

Câu 13 (2,5 điểm). Cho tam giác
ABC
vuông tại
,
A AB AC
đường cao
,
AH
đường vuông
góc với
AB
tại
B
cắt đường thẳng
AH
tại
M
.Cho
6 , 8
AB cm AC cm
.
a) Tính ,
BC AH
và các tỉ số lượng giác của góc
.
ACB
b) Tính diện tích tam giác
.
BMC
c) Đường thẳng qua
M
song song với
BC
cắt đường thẳng
AC
tại
N
. Gọi
K
là hình
chiếu của
M
trên
AN
. Chứng minh
2 2
. .
NA NK MK KN
Câu 14 (0,5 điểm). Cánh tay rô-bốt đặt trên mặt đất và có vị trí như hình vẽ, biết
60 ,
AB cm
60 , 32 , 53 .
BC cm BCN ABC
Tính độ cao của điểm
A
trên đầu cánh tay rô-bốt so với
mặt đất (làm tròn đến phần mười).
Câu 15 (1,0 điểm). Cho hai số thực
,
a b
thỏa mãn
0.
a b
Chứng minh
2
2 2 1
2.
ab
a b a b
…………………………..Hết……………………………
Giám thị coi thi không giải thích gì thêm

UBND HUYỆN BÌNH XUYÊN
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐÁP ÁN VÀ THANG ĐIỂM
ĐỀ THI ĐGCL MÔN TOÁN 9
Năm học: 2024 - 2025
I. TRẮC NGHIỆM (2 điểm): Mỗi câu đúng được 0,25 điểm
Câu 1 2 3 4 5 6 7 8
Đáp án D C A D B D B C
II. TỰ LUẬN (8 điểm)
Câu Nội dung đáp án Thang
điểm
9 (1,0
điểm)
Vì số nguyên tử ở hai vế được bảo toàn nên ta có:
1
3 2
x y
x y
Giải ra được
2, 3
x y
và kết luận
0,5
0,5
10 (1,5
điểm)
a)
2 3 1
3 2 9
x y
x y
Nhân phương trình thứ nhất với 3, phương trình thứ hai với 2 ta được :
6 9 3
6 4 18
x y
x y
Trừ theo từng vế của hai phương trình ta được:
5 15
y
3.
y
Thay vào phương trình thứ nhất ta được
2. 3. 3 1
x
5.
x
Vậy hệ phương trình có nghiệm là
5; 3
0,25
0,25
b)
5 2 5 0
x x x
5 2 0
x x
Suy ra
5 0
x
hoặc
2 0
x
5
x
hoặc
2
x
Vậy phương trình có nghiệm là
5
x
;
2
x
0,25
0,25
c)
2
1 1 8
1 1
1
x x
x x x
1 1 8
1 1
1 1
x x
x x x x (Điều kiện:
1; 1
x x
)
2 2
1 1 8
1 1 1 1 1 1
x x
x x x x x x
Suy ra
2 2
1 1 8
x x
2 2
2 1 2 1 8
x x x x
2 2
2 1 2 1 8
x x x x
4 8
x
2
x
(Thỏa mãn điều kiện)
Vậy phương trình có nghiệm là
2
x
0,25
0,25
11 (0,5
điểm)
Vì
a b
nên
2 2
a b
Do đó
3 2 3 2
a b
Vậy
3 2 3 2
a b
0,25
0,25
12 (1,0
điểm)
Gọi giá niêm yết của một chiếc bếp từ và một nồi chiên không dầu lần lượt
là
,
x y
(triệu đồng,
, 0
x y
)
Vì giá niêm yết một chiếc bếp từ và một nồi chiên không dầu có tổng số tiền
là
21
triệu đồng nên có phương trình:
21
x y
(1)
Giá một chiếc bếp từ sau khi giảm
15%
là:
85% 0,85
x x
(triệu đồng)
Giá một nồi chiên không dầu sau khi giảm
10%
là:
90% 0,9
y y
(triệu đồng)
Vì bác An đã mua hai sản phẩm sau khi giảm giá hết
18,3
triệu đồng nên có
phương trình
0,85 0,9 18,3
x y
(2)
Từ
(1)
,
(2)
ta có hpt:
0,85 0,9 18,3
21x y
x y
Giải phương trình ta được
12
9
x
y
(TM)
Vậy giá niêm yết của một chiếc bếp từ là
12
triệu đồng
Giá niêm yết của một nồi chiên không dầu là
9
triệu đồng
0,25
0,25
0,25
0,25
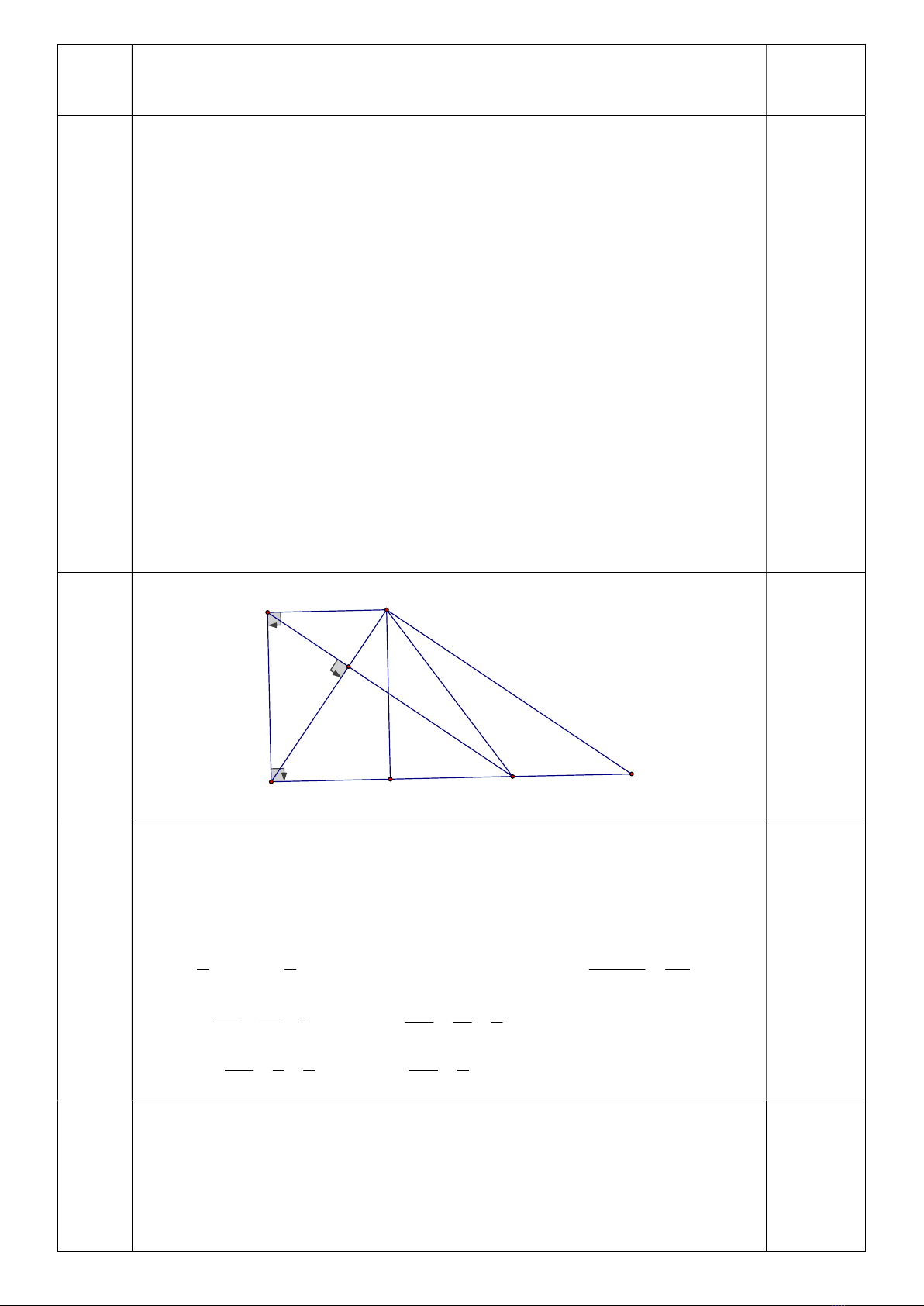
13 (2,5
điểm)
a) Tính ,
BC AH
và các tỉ số lượng giác của góc
ACB
.
Ta có:
ABC
vuông tại
A
nên
2 2 2
AB AC BC
(định lí Pi – ta – go)
2 2 2
6 8 100 10
BC BC cm
.
Ta có:
1 1 . 8.6
. . . . 4,8
2 2 10
ABC
AB AC
S AB AC AH BC AB AC AH BC AH cm
BC
6 3
sin ;
10 5
AB
ACB
BC
8 4
cos ;
10 5
AC
ACB
BC
6 3
tan ;
8 4
AB
ACB
AC
4
cot
3
AC
ACB
AB
0,25
0,25
0,25
0,25
b) Tính diện tích tam giác
BMC
.
Ta có:
AHB
vuông tại
H
nên
2 2 2
2 2 2
2 2
8 4,8 40,96
AB AH HB
HB AB AH
K
N
M
H
B
C
A

3,6
HB cm
Xét
HBM
và
HAB
có
tan
HB
HAB
AH
;
tan
HM
HBM
HB
, mà
HBM HAB
(cùng phụ với
HBA
) nên
tan tan
HAB HBM
.
Do đó
2 2
3,6
2,7
4,8
HB HM HB
HM cm
HA HB HA
.
2
1 1
. 2,7.10 13,5
2 2
BMC
S HM BC cm
.
Chú ý: HS có thể giải theo cách chứng minh tam giác đồng dạng.
0,25
0,25
0,25
0,25
c) Chứng minh
2 2
.
NA NK MK KN
.
Xét
KNM
và
MNA
có tan
KN NM
N
MN NA
Suy ra
2
. 1
MN NA NK
Xét
MKN
vuông tại
K
có:
2 2 2
MN MK KN
(định lí Pi – ta – go) (2)
Từ (1) và (2) suy ra:
2 2
.
NA NK MK KN
.
Chú ý: HS có thể giải theo cách chứng minh tam giác đồng dạng.
0,25
0,25
14 (0,5
điểm) Vì
/ /
BM NC
(cùng vuông góc với
BN
) nên
32
CBM BCN
(2 góc so le
trong), suy ra
53 32 21
ABM CBM BCM
NBC
vuông tại
N
có:
.sin 60.sin32 31,8
NB BC NCB cm
AMB
vuông tại
M
có:
.sin 60.sin 21 21,5
AM AB ABM cm
Vậy độ cao của điểm A trên đầu cánh tay rô-bốt so với mặt đất là:
17 31,8 21,5 70,3
CP BN AM cm
0,25
0,25
15 (1,0
điểm)
Với hai số thực
,
a b
thỏa mãn
0
a b
, ta có:
2
2 2 1
2
ab
a b a b
2 2 2
2 2 1 2
a b a b ab a b
2 2 2 2
2 1 2 0
a b a b ab ab a b
4 2 2 2
2 1 2 0
a b ab a b ab a b
4 2 2
2 1 1 0
a b a b ab ab
2
2
1 0
a b ab
(luôn đúng với mọi số thực
,
a b
).
0,25
0,25
0,25
0,25
LƯU Ý CHUNG
- Hướng dẫn chấm chỉ trình bày một cách giải bao gồm các ý bắt buộc phải có trong bài làm của
học sinh. Khi chấm nếu học sinh bỏ qua bước nào thì không cho điểm bước đó.
- Nếu học sinh giải cách khác, giám khảo căn cứ các ý trong hướng dẫn chấm để cho điểm.
- Câu 13 không vẽ hình hoặc vẽ sai hình không cho điểm.
- Câu 14 học sinh có thể không cần vẽ lại hình.
- Trong bài làm, nếu ở một bước nào đó bị sai thì các phần sau có sử dụng kết quả sai đó không
được điểm.
- Điểm toàn bài tính đến hai chữ số thập phân.







![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)




![Đề thi học kì 2 Vật lý lớp 11: Đề minh họa [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250709/linhnhil/135x160/711752026408.jpg)



