ĐỀ THI MÔN BI N Đ I TÍN HI U SẾ Ổ Ệ Ố
Đề s : 061 - Th i gian: 45 phútố ờ
Cđu 1: Tín hi u ệ
)n2(u)n(u −
lă câch vi t khâcế
c a tín hi u:ủ ệ
)3n()2n()1n()n( −δ+−δ+−δ+δ
)3n()1n()n( −δ+−δ+δ
)3n()2n()n( −δ+−δ+δ
)2n()1n()n( −δ+−δ+δ
Cđu 2: Ba m u đ u tiín c a đâp ng xung c aẫ ầ ủ ứ ủ
h nhđn qu :ệ ả
)1n(x)n(x)1n(y3.0)n(y −−=−−
l n l t lă:ầ ượ
1 , 0.7 , - 0.21 1 , 0.7 ,
0.21
1 , - 0.7 , - 0.21 1 ,- 0.7 ,
0.21
Cđu 3: Cho hai h th ng:ệ ố
(1)
)2n(x5)1n(x3)n(x2)n(y −−−+=
(2)
)2n(x5)1n(x3)n(x2)n(y 222 −−−+=
C hai đ u tuy n tínhả ề ế C hai đ u phiả ề
tuy nế
Ch có h (2) tuy n tính ỉ ệ ế
Ch có h (1) tuy n tínhỉ ệ ế
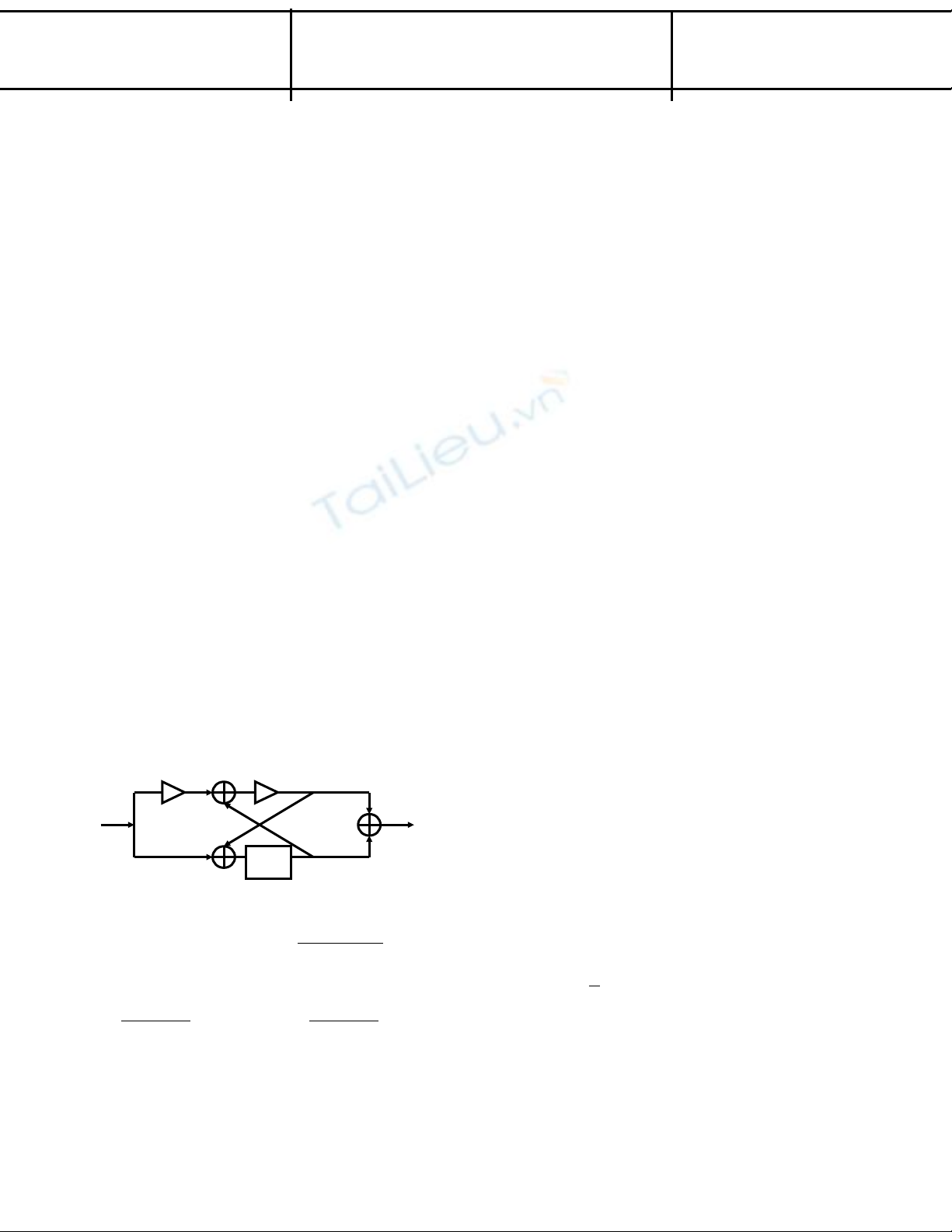
Cđu 4: Cho h th ng:ệ ố
Hăm truy n đ t c a h năy lă:ề ạ ủ ệ
a−
1
1
z1
aza
−
−
+
−
1
1
z1
aza
−
−
+
+
Cđu 5: Cho hai tín hi u ệ
{ }
0,0,0,0,1,1,1,1)n(x1↑
=
vă
{ }
1,1,0,0,0,0,1,1)n(x2↑
=
. Quan h gi a ệ ữ X1(k)
vă X2(k) lă:
)k(X)j()k(X 2
k
1=
)k(X)j()k(X 2
k
1−=
)k(X)1()k(X 2
k
1−=
)k(X)k(X 21 =
Cđu 6: Cho
{ }
7,6,5,4,3,2,1,0)n(x ↑
=
. Từ
l u đ thu t toân FFT phđn th i gian ư ồ ậ ờ N = 8, suy ra
X(7) lă:
)WWW1(4 3
8
2
88 ++−−
)WWW1(4 3
8
2
88 −−−−
)WWW1(4 3
8
2
88 +−−−
)WWW1(4 3
8
2
88 +++−
Cđu 7: Tín hi u t ng t đ c l y m u v i t nệ ươ ự ượ ấ ẫ ớ ầ
s ố16 kHz r i tính DFT ồ512 m u. T n s (Hz) t iẫ ầ ố ạ
v ch ph ạ ổ k = 64 lă:
64 1968.75 2000
2031.25
Cđu 8: B l c nhđn quộ ọ ả:
y(n) - 0.2 y(n-1) = x(n) - x(n-2) có đâp ng xungứ
lă:
)]2n(u)n(u[2.0
n
−−
)]2n(u)n(u[2.0
2n
−−
−
)]2n(u5)n(u[2.0
n
−−
)]2n(u25)n(u[2.0
n
−−
Cđu 9: Cho hai h th ng:ệ ố
(1)
[ ]
)2n(x)1n(x)n(x
3
1
)n(y −+−+=
(2)
)2n(y02.0)1n(y2.0)n(x)n(y −−−+=
H (1) không đ quy, h (2) đ quyệ ệ ệ ệ
H (1) đ quy, h (2) không đ quy ệ ệ ệ ệ
C hai h đ u đ quy ả ệ ề ệ
C hai h đ u không đ quyả ệ ề ệ
-1
a
z - 1
ĐỀ THI MÔN BI N Đ I TÍN HI U SẾ Ổ Ệ Ố
Đề s : 061 - Th i gian: 45 phútố ờ
Cđu 10: Cho tín hi u ệ
)n(u
4
n
cos π
đi qua b l cộ ọ
có đâp ng xung ứ
)2n(3)1n()n(2 −δ+−δ−δ
Tín hi u ra t i ệ ạ n = 1 lă:
0 0.41 1 -
0.41
Cđu 11: Cho
2
j
2j
j
e
2
1
1
e
)e(X
−
=ω−
ω−
ω
.
Đđy lă ph c a tín hi u sau:ổ ủ ệ
)1n(u
2
1
)1n(
2n
−
−
−
)2n(u
2
1
)1n(
2n
−
−
−
C ả vă đ u đúng ề C ả vă đ uề
sai
Cđu 12: Cho
{ }
3,2,1,0)n(x 4↑
=
vă câc quan
h sau:ệ
})n(y{DFT)k(X)k(Y};)n(x{DFT)k(X
4
2
4
===
Tín hi u ệ
4
)n(y
lă:
}8,6,8,14{ ↑
}4,10,12,10{ ↑
}8,6,8,10{ ↑
}10,12,8,4{↑
Cđu 13: Cho tín hi u ệ
ncos
2
3
)n(x π=
n∀
đi
qua h th ng ệ ố
)n(u)5.0()n(h n
=
. Tín hi u raệ
lă:
x(n)
)n(x
2
3
)n(x
3
2
2
3
n∀
Cđu 14: M t b l c nhđn qu t o tín hi u sinộ ộ ọ ả ạ ệ
t n s ầ ố
0
ω
có hăm truy n đ t lă:ề ạ
1cosz2z
sinz
)z(H
0
2
0
+ω−
ω
=
Dùng b l c năyộ ọ đ t oể ạ
tín hi u sin ệ2 kHz v i t n s l y m u ớ ầ ố ấ ẫ 8 kHz. Khi
tín hi u văo lă xung dirac, tín hi u ra lă: ệ ệ
)n(u)n
2
sin( π
)n(u)n
2
cos( π
)n
2
sin( π
)n
2
cos( π
Cđu 15: Cho tín hi u ệ
)n(u)
2
n
sin()n(u2 π
+
đi
qua h th ng FIR ệ ố
)1n(x5.0)n(x)n(y −+=
.
Tín hi u ra t i ệ ạ n = 1 lă:
0 4 2
1
Cđu 16: Cho
21 )z25.01(
1
)z(X −
+
=
. Đđy lă bi nế
đ i Z c a hăm x(n) nhđn qu sau:ổ ủ ả
)n(u)25.0)(1n( n
−+
)n(u)25.0(n n
−
)n(u)25.0)(1n( n
−−
)n(u)25.0(n n
Cđu 17: H th ngệ ố
)2n(x)1n(y6.0)n(y −=−+
n đ nh Ổ ị Không nổ
đ nhị
Ổn đ nh v i đi u ki n h nhđn qu ị ớ ề ệ ệ ả
n đ nh v i đi u ki n h không nhđn quỔ ị ớ ề ệ ệ ả
Cđu 18: Tín hi u t ng t đ c l y m u v i t nệ ươ ự ượ ấ ẫ ớ ầ
s ố44.1 kHz r i tính DFT v i kích th c c a sồ ớ ướ ử ổ
DFT lă 23.22 ms. Đ phđn gi i c a DFT (tínhộ ả ủ
b ng Hz) lă:ằ
40.07 43.07 42.07
41.07
ĐỀ THI MÔN BI N Đ I TÍN HI U SẾ Ổ Ệ Ố
Đề s : 061 - Th i gian: 45 phútố ờ
Cđu 19: Cho tín hi u ệ
{ }
1,1,1)n(x ↑
=
đi qua hệ
th ng l c phđn chia h s M = 2, đâp ng xungố ọ ệ ố ứ
c a b l c lă: ủ ộ ọ
)3n(
4
1
)2n(
4
2
)1n(
4
3
)n()n(h
−δ+−δ+−δ+δ=
Tín hi u ra h th ng trín ệ ệ ố
)n(y 2H↓
lă:
)2n(
4
3
)1n(
4
9
)n( −δ+−δ+δ
)1n(
4
9−δ
)1n(
4
9
)n( −δ+δ
)2n(
4
3−δ
Cđu 20: B l c Haar có hăm truy n đ t lă:ộ ọ ề ạ
1
z
2
1
2
1
−
−−
1
z
2
1
2
1
−
−
1
z
2
1
2
1
−
+
1
z
2
1
2
1
−
+−