1
TRƯỜNG THPT HÒA ĐA
ĐỀ THI HỌC KÌ II NĂM HỌC 2008 – 2009
MÔN THI: TOÁN 12
Thời gian làm bài 150 phút
I. PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7 điểm)
Bài 1:(3 điểm)
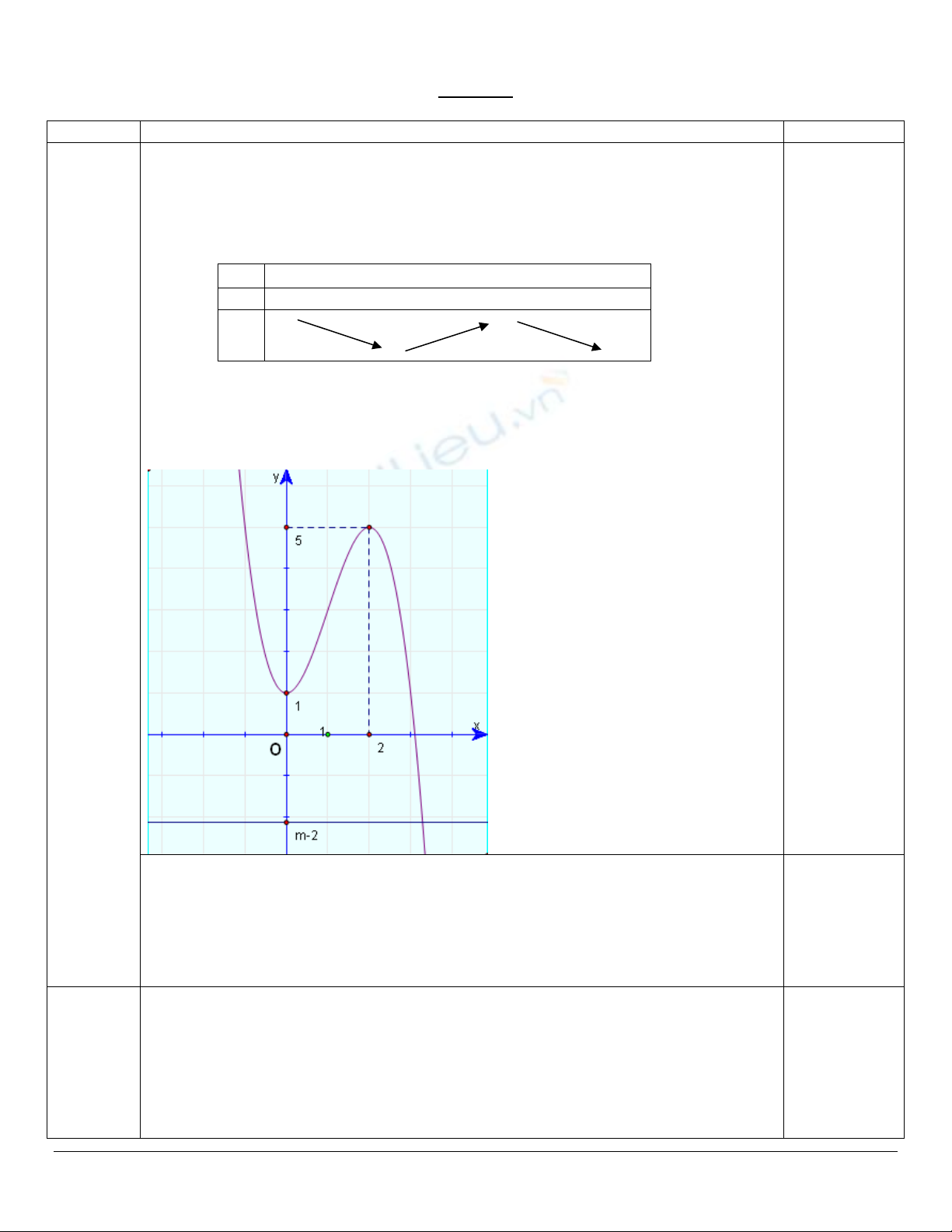
Cho hàm số y = – x3 + 3x2 + 1.
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2) Dùng đồ thị (C), biện luận số nghiệm của phương trình sau theo tham số m :
– x3 + 3x2 + 3 – m = 0
Bài 2: (3 điểm)
1) Giải phương trình sau:
9 5.3 6 0
x x
2) Tính tích phân sau:
4
0
1 3sin 2
.cos 2 .
x
x dx
3) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x4 – 8x2 + 16 trên đoạn [ -1 ; 3]
Bài 3: (1 điểm)
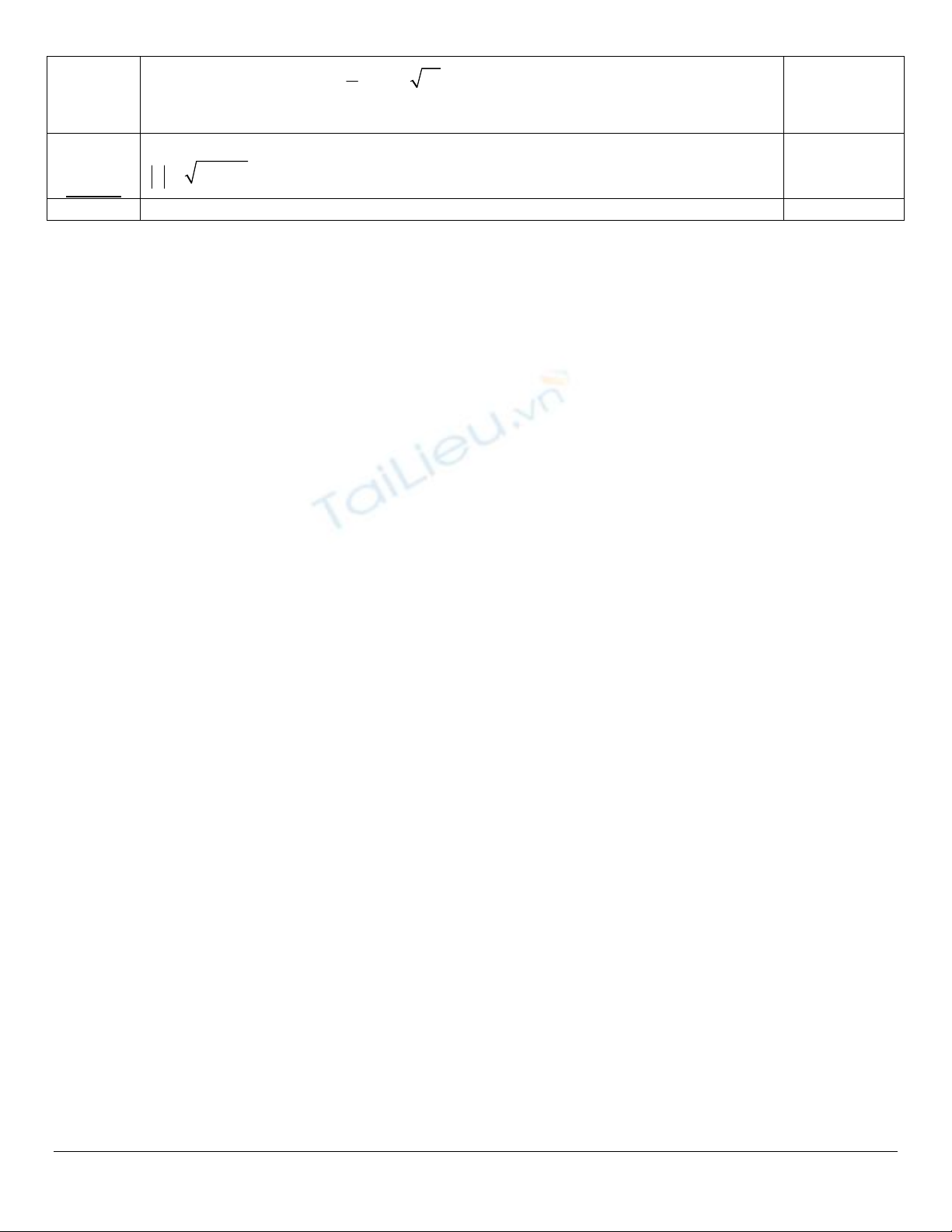
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc giữa cạnh bên với mặt đáy bằng .
Tính thể tích khối chóp S.ABCD theo a và .
II. PHẦN RIÊNG (3 điểm)
Thí sinh học chương trình nào thì chỉ được làm phần dành riêng cho chương trình đó (phần 1 hoặc
phần 2)
1) Theo chương trình cơ bản:
Bài 4:(2 điểm)
Trong không gian Oxyz, cho các điểm M(2; 5; -3), N(4; -3; 1) và
mặt phẳng
( )
: x – 2y – z + 1 = 0
1) Viết phương trình mặt phẳng (P) đi qua hai điểm M, N và vuông góc với mặt phẳng
( )
.
2) Viết phương trình mặt cầu (S) đường kính MN.
Bài 5:(1 điểm)
Cho số phức z = (2 – 3i)(1 + 2i) – 5 + 3i. Xác định phần thực, phần ảo và tính môđun số phức z.
2) Theo chương trình nâng cao:
ĐỀ SỐ 2
2
Bài 4:(2 điểm)
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(– 1; –2; 3), B(2; – 3; – 1), C(– 3; 2; –
1), D(– 2; 0; – 3).
1) Chứng minh A, B, C, D là bốn đỉnh của một tứ diện. Tính thể tích khối tứ diện ABCD.
2) Viết phương trình của mặt phẳng (BCD).
3) Viết phương trình mặt cầu (S) tâm A và tiếp xúc với mặt phẳng (BCD). Tìm tọa độ tiếp điểm.
Bài 5:(1 điểm) Tính (1 + i)15
3
ĐÁP ÁN ĐỀ THI HỌC KÌ II MÔN TOÁN LỚP 12 NĂM HỌC 2008 – 2009
ĐỀ SỐ 2
Nội dung
Thang điểm
Bài 1
(3 điểm)
a)Hàm số y = - x
3
+ 3x
2
+ 1
MXĐ:
y’ = - 3x2 +6x; y’ = 0
0 1
2 5
x y
x y
; lim
xy

Bảng biến thiên
x -
0 2 +
y’ – 0 + 0 –
y +
CT 5
1 CĐ -
Hàm số đồng biến trên các khoảng (0 ; 2).
Hàm số nghịch biến trên các khoảng (- ; 0), (2 ; +)
Hàm số đạt cực đại tại xCĐ = 2 và yCĐ = 5
Hàm số đạt cực đại tại xCT = 0 và yCT = 1
Đồ thị: Đồ thị là một đường cong có tâm đối xứng là điểm I(1 ; 3)
0,5 đ
0,5đ
0,5đ
0,5 đ
b)Pt: - x
3
+ 3x
2
+ 3 – m = 0
- x
2
+ 3x
2
+ 1 = m – 2 (*)
Phương trình (*) là phương trình hoành độ giao điểm giữa đồ thị (C) với đường
thẳng : y = m. Dựa vào đồ thị ta có:
+ khi m< 3 hay m>7: phương trình có 1 nghiệm.
+ khi m= 3 hay m= 7: phương trình có 2 nghiệm.
+ khi 3 < m< 7: phương trình có 3 nghiệm.
0,25đ
0,25đ
0,5đ
Bài 2
(3 điểm)
a) Đặt t = 3
x
, điều kiện: t > 0. Phương trình trở thành
t2 – 5t + 6 = 0 t1 = 3 ; t2 = 2.
Với t1 = 3 ta có: 3x = 3 x = 1
Với t2 = 2 ta có: 3x = 2 x =
3
log 2
0,5đ
0,5đ
0,25đ
4
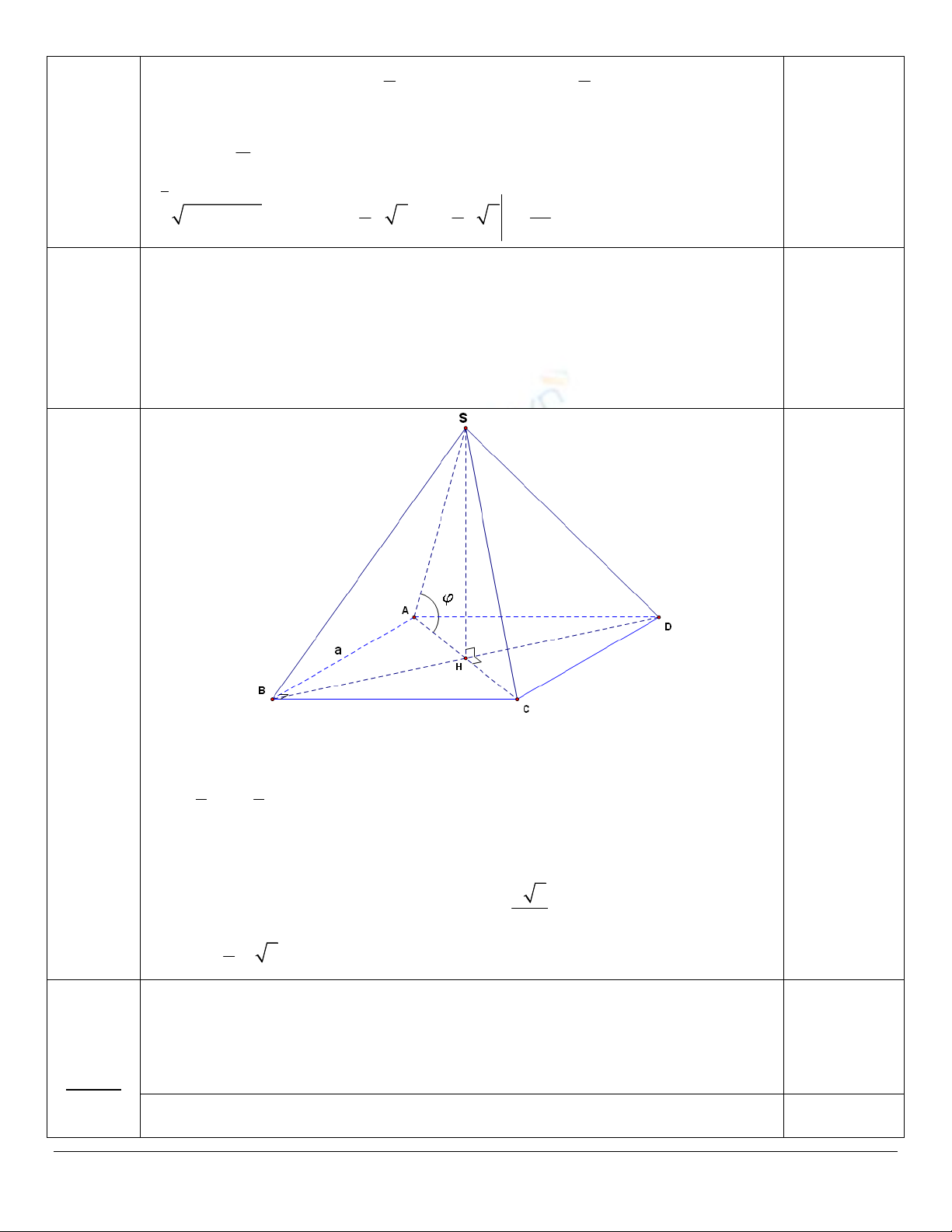
b) Đặt u = 1 + 3sin2x
3 2
cos 2 . cos 2 .
2 3
du x dx x dx du
Khi x = 0 u = 1
Khi x =
4
u = 4
4
4
4
1
0 1
2 4 28
1 3sin 2
3 9 9
.cos 2 . .x u u ux dx du
0,25đ
0,5đ
c) y’ = 4x3 – 16x ; cho
0 1;3
' 0 2 1;3
2 1;3
x
y x
x
y(-1) = 9; y(0) = 16; y(2) = 0; y(3) = 25
1;3
Maxy = y(3) =25
2;2
Miny = y(2) =0
0,25đ
0,25đ
0,5đ
Bài 3
(1 điểm)
Gọi H là hình chiếu của đỉnh S lên (ABC). Khi đó H trùng với tâm đa giác đáy
Thể tích khối chóp S.ABCD
2
1 1
. .
3 3
V B h a SH
AH là hình chiếu của AS lên mp(ABC)
,( ) ;SA ABC SA AH SAH
Tam giác SAH vuông tại H nên SH = AH.tan=2
tan
2
a
Vậy: 3
1
2.tan
6
V a
0,25đ
0,25đ
0,25đ
0,25đ
Bài 4
(2 điểm)
Phần 1
a) Vectơ pháp tuyến của mp(
) là
( 1; 2;1)
u
(2; 8; 4)
MN
Vectơ pháp tuyến của mp(P) là
(8;3; 2)
P
n
Phương trình mp(P): 8x + 3y + 2z - 25 = 0.
0,25đ
0,25đ
0,5đ
b) Tọa độ tâm mặt cầu (S) là I(3 ; 1; -1) 0,25đ
5
Bán kính mặt cầu (S): 1
21
2
r MN
Phưong trình mặt cầu (S): 2 2 2
( 3) ( 1) ( 1) 21
x y z
0,25đ
0,5đ
Bài 5
(1 điểm)
Phần 1
z =(2 – 3i)(1 + 2i) – 5 + 3i = 3 + 4i.
2 2
3 4 5
z
0,5đ
0,5đ