Đề thi môn Toán lớp 11 năm học 2018 – 2019 (Mã đề thi 156, có lời giải chi tiết)

Trang 1/11 - Mã đề thi 156

TRƯỜNG THPT ………….

TỔ TOÁN

BÀI:………………….

NĂM HỌC 2018 – 2019

Môn: Toán - Lớp 11 - Chương trình chuẩn

ĐỀ CHÍNH THỨC Thời gian: ……… phút

Mã đề thi

156

Họ và tên:

………………………………………….

Lớp:

……………...……..………

Câu 1. Định

để đồ thị hàm số 3 2

y x mx

  

tiếp xúc với đường thẳng

: 5

d y



. B.

 

. C.



. D.

 

Lời giải

Chọn B

Đường thẳng 3 2

y x mx

  

và đồ thị hàm số



tiếp xúc nhau

3 2

1 5 (1)

3 2 0 (2)

x mx

  



 





có nghiệm.

(2) (3 2 ) 0

x x m







    



+ Với



thay vào

(1)

không thỏa mãn.

+ Với

x thay vào

(1)

ta có: 3

27 3

m m

    

Câu 2. Cho hàm số





có đồ thị

 

. Viết phương trình tiếp tuyến của

 

, biết tiếp tuyến tạo với

hai trục tọa độ một tam giác có diện tích bằng

9 1

4 2

y x

  

;

4 1

9 9

y x

  

. B.

9 31

4 2

y x

  

;

4 2

9 9

y x

  

9 1

4 2

y x

  

;

4 4

9 9

y x

  

. D.

9 1

4 2

y x

  

;

4 2

9 9

y x

  

Lời giải

Chọn D

Hàm số xác định với mọi

2x 

Ta có:

( 2)



Gọi 0 0

( ; ) ( )M x y C

. Tiếp tuyến



của

 

tại

có phương trình

0 0

2 2 2

0 0 0

2 2

4 4

( ) 2

( 2) ( 2) ( 2)

x x

y x x x

x x x

    



  

Gọi

,A B

lần lượt là giao điểm của tiếp tuyến



với

,Ox Oy

Suy ra 2

2 2

0 0

( 2) ( 2) 0

x x

x x y

 



 

 

   

  





( ;0)

A x 

: 0;

( 2)

B B

 

 



 



 



 





Vì 0

, 0

A B O x

  

Trang 2/11 - Mã đề thi 156

Tam giác AOB vuông tại O nên

1 1

2 2

( 2)

AOB

S OA OB x

  

Suy ra

4 2

0 0

9 9 ( 2)

18 ( 2)

AOB

S x x

     



0 0

3 2 0 (vn)

3 2 0

x x

 

   

 



 

  







* 0 0 0

2 4

1 , '( )

3 9

x y y x

   

. Phương trình

4 2

9 9

y x

  

* 0 0 0

2 9

1, '( )

3 4

x y y x

     

Phương trình

9 2 9 1

: ( ) 1

4 3 4 2

y x x

     

Câu 3. (THPT Chuyên Vĩnh Phúc- Lần 3-2018) Cho đồ thị hàm số

   

3 2

: 2 3 5   

C y f x x x . Từ

điểm 19

 

 

 

A kẻ được bao nhiêu tiếp tuyến tới

 

. B.

. C.

. D.

Lời giải

Chọn C

Gọi

hệ số góc của tiếp tuyến đi qua 19

 

 

 

A tới

 

Phương trình tiếp tuyến

 



là: 19

 

  

 

 

y k x .

 



tiếp xúc với

 

3 2

2 3 5 4, 1

6 6 , 2

 

    

 

 



 



x x k x

x x k

có nghiệm

Thay

từ

 

vào

 

ta được:

 

3 2 2 19

2 3 5 6 6 4

 

     

 

 

x x x x x

 

3 2 2

4 6 19 2 12 19

      x x x x x x

3 2

8 25 19 2 0    

x x x









 









. Vậy từ điểm 19

 

 

 

A kẻ được

tiếp tuyến tới

 

Câu 4. (THPT Chu Văn An - Hà Nội - Lần 1 - 2017 - 2018 - BTN) Cho hàm số 3 2

3 1

y x x x

   

có

đồ thị là

 

. Có tất cả bao nhiêu giá trị nguyên của tham số

để từ điểm

 

0;M m

kẻ được ít

nhất một tiếp tuyến đến đồ thị

 

mà hoành độ tiếp điểm thuộc đoạn

 

1;3

B. Vô số C.

Lời giải

Chọn C

Ta có 2

3 2 3y x x



  

Gọi

 

;

x y

là tọa độ tiếp điểm. Phương trình tiếp tuyến có dạng:

  

0 0 0

y y x x x y



  

 

2 3 2

0 0 0 0 0 0

3 2 3 3 1

y x x x x x x x

        

Vì tiếp tuyến qua

 

0;M m

nên ta có

 

2 3 2

0 0 0 0 0 0

3 2 3 0 3 1

m x x x x x x

       

 

3 2

0 0

2 1 1

m x x     .

Trang 3/11 - Mã đề thi 156

Để từ điểm

 

0;M m kẻ được ít nhất một tiếp tuyến đến đồ thị

 

C mà hoành độ tiếp điểm thuộc

đoạn

 

1;3 thì phương trình

 

1 có ít nhất một nghiệm

 

1;3x

Xét hàm số

 

3 2

2 1y f t t t     trên đoạn

 

1;3 suy ra

 

6 2 0 1

f t t t t







      



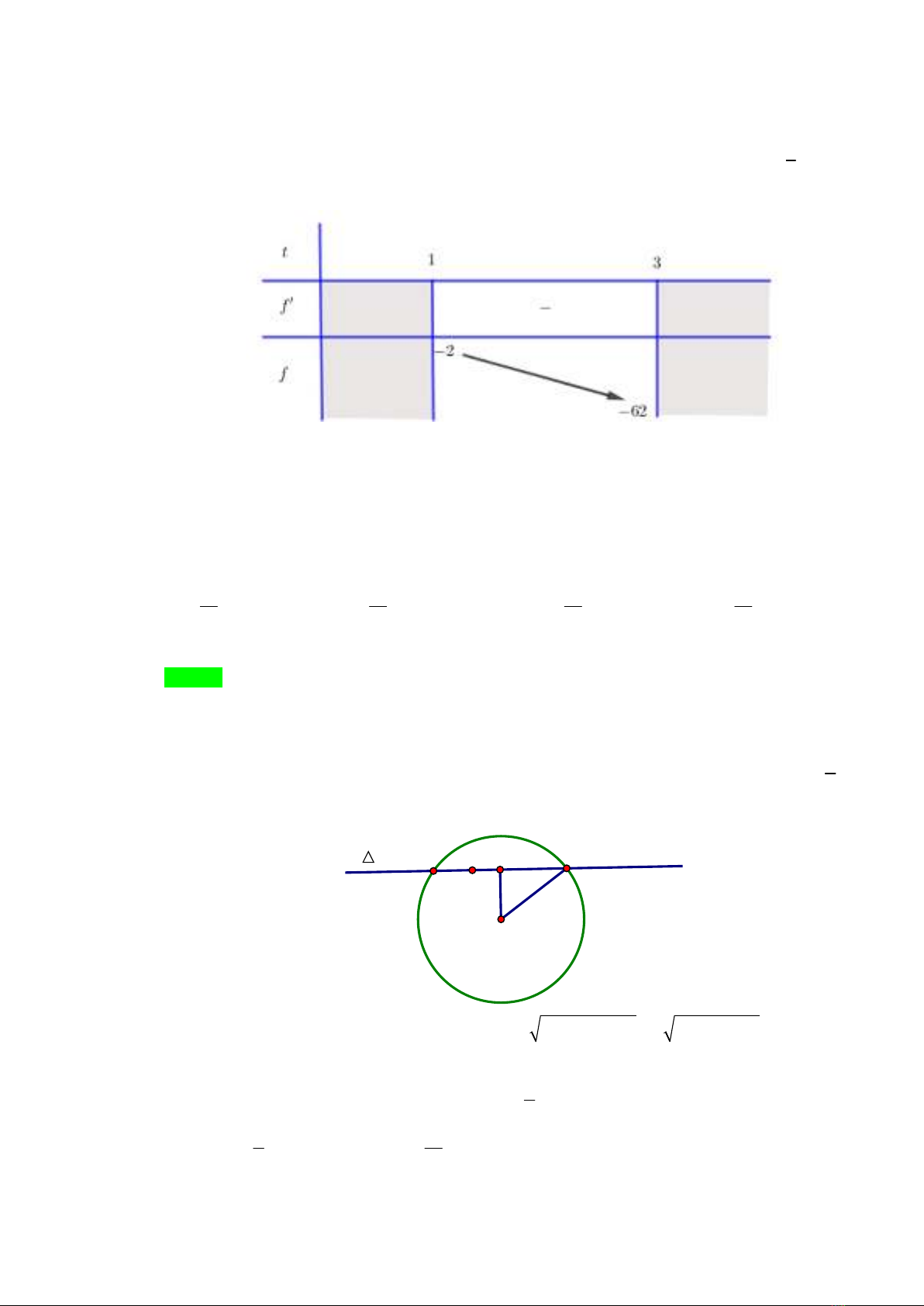
Bảng biến thiên:

Dựa vào bảng biến thiên ta có

62 2m   

Vậy có tất cả

giá trị nguyên của tham số

thỏa mãn yêu cầu bài toán.

Câu 5. (THPT Lê Hồng Phong - Nam Định - Lần 1 - 2017 - 2018 - BTN) Cho hàm số

4 2

2y x mx m   , có đồ thị

 

C với

là tham số thực. Gọi

là điểm thuộc đồ thị

 

C có

hoành độ bằng

. Tìm

để tiếp tuyến



với đồ thị

 

C tại

cắt đường tròn

   

: 1 4x y



  

tạo thành một dây cung có độ dài nhỏ nhất



. B.

. C.



. D.

Lời giải

Chọn D

Đường tròn

   

: 1 4x y



  

có tâm

 

0;1I,

2R

Ta có

 

1;1A m;

 

4 4 1 4 4y x mx y m

 

     .

Suy ra phương trình



  

4 4 1 1y m x m     . Dễ thấy



luôn đi qua điểm cố định

3;0

F 

 

 

và điểm

nằm trong đường tròn

 



Giả sử



cắt

 



tại

. Thế thì ta có:

   

2 2 2

2 ; 2 4 ;MN R d I d I      .

Do đó

nhỏ nhất

 

;d I  lớn nhất

 

;d I IF  

IF  

Khi đó đường



có 1 vectơ chỉ phương

3; 1

u IF  

  

 

 





;

 

1; 4 4u m 

 nên ta có:

 

. 0 1. 4 4 0

u n m    

  13

m 

Trang 4/11 - Mã đề thi 156

Câu 6. Cho hàm số

2 1







.Tìm giá trị nhỏ nhất của m sao cho tồn tại ít nhất một điểm



 

mà

tiếp tuyến của

 

tại

tạo với hai trục toạ độ một tam giác có trọng tâm nằm trên đường thẳng

: 2 1d y m 

. B.

. C.

. D.

Lời giải

Chọn A

Gọi 0 0

( ; ) ( )M x y C

. Phương trình tiếp tuyến tại

0 0

( )

(2 1)

y x x y



  



Gọi

là giao điểm của tiếp tuyến với trục hoành và trục tung



0 0

2 4 1

(2 1)

x x

 

.

Từ đó trọng tâm

của

OAB

có:

0 0

2 4 1

3(2 1)

x x

 

.

Vì

G d

nên

0 0

2 4 1

2 1

3(2 1)

x x m

 

 



Mặt khác:

2 2 2 2

0 0 0 0 0

2 2 2

0 0 0

2 4 1 6 (2 1) 6

1 1

(2 1) (2 1) (2 1)

x x x x x

x x x

   

    

  

Do đó để tồn tại ít nhất một điểm

thỏa bài toán thì

1 1

2 1

3 3

m m

    

Vậy GTNN của

là

Câu 7. Cho hàm số

 

f x x  

, có đồ thị

 

. Từ điểm

 

2; 1



kẻ đến

 

hai tiếp tuyến phân

biệt. Hai tiếp tuyến này có phương trình:

1y x 

và

3y x  

. B.

1y x  

và

3y x 

2 5y x 

và

2 3y x  

. D.

1y x  

và

3y x  

Lời giải.

Chọn B

Gọi

 

0 0

;

N x y

là tiếp điểm;

0 0

y x

  

;

 

f x



 

Phương trình tiếp tuyến tại

là:

 

0 0

1 1

2 4

x x

y x x x

 

     

 

 

Mà tiếp tuyến đi qua

 

2; 1



 

2 2

0 0 0

1 1 2 1 0

2 4 4

x x x

 

           

 

 

 

0 0

0; 1; 0 1

4; 1; 4 1

x y f



   





  





Phương trình tiếp tuyến :

1y x  

và

3y x 

Câu 8. (THPT Mộ Đức 2 - Quảng Ngãi - 2017 - 2018 - BTN)Cho hàm số

 

y f x

 có đạo hàm tại

1x

. Gọi

lần lượt là tiếp tuyến của đồ thị hàm số

 

y f x

 và

   

2 1

y g x xf x

  

tại

điểm có hoành độ

1x

. Biết rằng hai đường thẳng

vuông góc với nhau, khẳng định nào sau

đây đúng

Trang 5/11 - Mã đề thi 156

 

1 2 2f

. B.

 

2 1 2 2f 

. C.

 

2 1 2f 

. D.

 

1 2f

Lời giải

Chọn A

Ta có:

     

2 1 2 . 2 1g x f x x f x

 

   

     

1 1 2 1g f f

 

   .

d có hệ số góc là

 

1f.

d có hệ số góc là

     

1 1 2 1g f f

 

  .

Mà

1 2

d d

   

1 . 1 1f g

 

  

     

1 . 1 2 1 1f f f

 

    

 

   

 

2 1 1



 

 

 

  

(do

 

1 0f)

   

 

2 1 1

 

 

  

Xét hàm số

 

2 1t

h t t





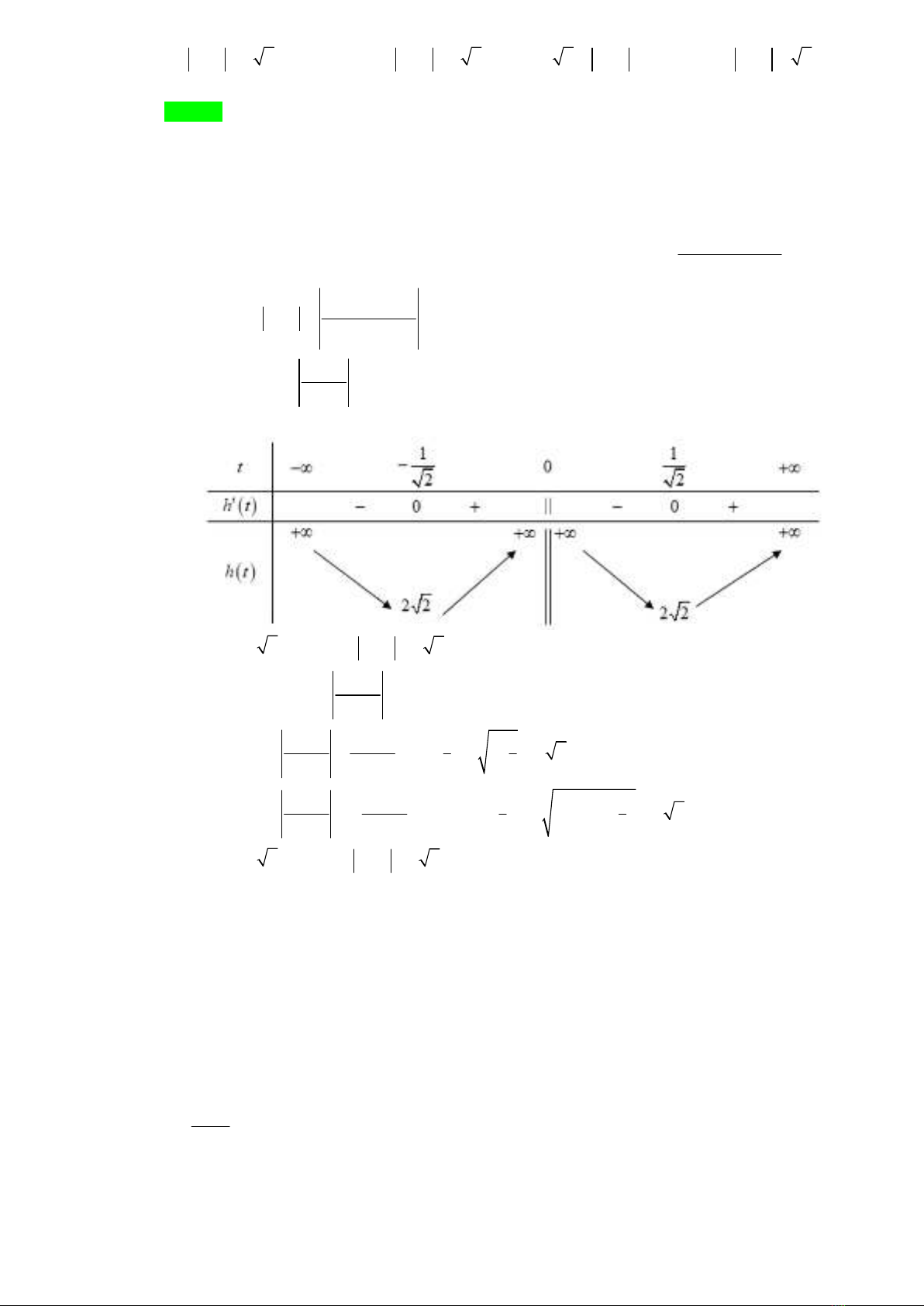
BBT:

Vậy

 

2 2h t 

0t 

 

1 2 2f 

Cách khác: Xét

 

2 1t

h t t





Với

0t

ta có:

2 2

2 1 2 1 1 1

2 2 2 . 2 2

t t t t

 

    

Với

0t

ta có:

   

2 2

2 1 2 1 1 1

2 2 2 . 2 2

t t t t

     

         

   

    .

Vậy

 

2 2h t 

0t 

 

1 2 2f 

Câu 9. Cho hàm số

1 ( 1)y x m x    có đồ thị là ( )

C. Có bao nhiêu giá trị

để tiếp tuyến của ( )

tại giao điểm của nó với trục tung tạo với hai trục tọa độ một tam giác có diện tích bằng

. B.

. C.

. D.

Lời giải

Chọn D

Ta có

(0;1 )M m

là giao điểm của ( )

C với trục tung

' 3 '(0)y x m y m    

Phương trình tiếp tuyến với ( )

C tại điểm

là

1y mx m   

Gọi A, B lần lượt là giao điểm của tiếp tuyến này với trục hoanh và trục tung, ta có tọa độ

1; 0

  

 

  và

(0;1 )B m

Đề thi môn Toán lớp 11 năm học 2018 – 2019 (Mã đề thi 156, có lời giải chi tiết)

Có thể bạn quan tâm

Tài liêu mới

Giới thiệu

Về chúng tôi

Việc làm

Quảng cáo

Liên hệ

Chính sách

Thoả thuận sử dụng

Chính sách bảo mật

Chính sách hoàn tiền

DMCA

Hỗ trợ

Hướng dẫn sử dụng

Đăng ký tài khoản VIP

093 303 0098

support@tailieu.vn

Phương thức thanh toán

Theo dõi chúng tôi

Facebook

Youtube

TikTok

Đề thi môn Toán lớp 11 năm học 2018 – 2019 (Mã đề thi 156, có lời giải chi tiết)

Có thể bạn quan tâm

Tài liêu mới

AI tóm tắt

Giới thiệu tài liệu

Đối tượng sử dụng

Từ khoá chính

Nội dung tóm tắt

Giới thiệu

Về chúng tôi

Việc làm

Quảng cáo

Liên hệ

Chính sách

Thoả thuận sử dụng

Chính sách bảo mật

Chính sách hoàn tiền

DMCA

Hỗ trợ

Hướng dẫn sử dụng

Đăng ký tài khoản VIP

093 303 0098

support@tailieu.vn

Phương thức thanh toán

Theo dõi chúng tôi

Facebook

Youtube

TikTok