-Trang 1
Đ THI MÔN X LÝ TÍN HI U SỀ Ử Ệ Ố
Đ S 054 (Th i gian: 70 phút)Ề Ố ờ
Câu 1:
{ }
j22,2,j22,6)k(X 4−−−+−= ↑
là
ph r i r c c a ổ ờ ạ ủ x(n)4. Năng l ng c aượ ủ x(n)4 là:
14
2
2
4
2
1 4
Câu 2: Cho tín hi u ệ
n
)1(
2
3
)n(x −=
n
∀
đi qua
hệ
th ng có ố
)n(u)5.0()n(h n
=
. Tín hi u ra là:ệ
n
)1(−
n
∀
n
)1(
2
3−
n∀
n
)1(
3
2−
n∀
2
3
n∀
Câu 3: Ph ng trình c a b l c s thông th pươ ủ ộ ọ ố ấ
t n s c t ầ ố ắ 2.5 kHz, t n s l y m u ầ ố ấ ẫ 10 kHz thi tế
k b ng ph ng pháp c a s ch nh t ế ằ ươ ử ổ ữ ậ N = 7
là:
)3n(x
2
1
)]4n(x)2n(x[
1
)]6n(x)n(x[
3
1
)n(y
−+−+−
π
−−+
π
−=
)3n(x
2
1
)]4n(x)2n(x[
1
)]6n(x)n(x[
3
1
)n(y
−+−+−
π
+−+
π
=
)3n(x
2
1
)]4n(x)2n(x[
1
)]6n(x)n(x[
3
1
)n(y
−+−+−
π
+−+
π
−=
Câu 4: M t b l c nhân qu t o tín hi u sin t nộ ộ ọ ả ạ ệ ầ
số
0
ω
có hàm truy n đ t là:ề ạ
1cosz2z
sinz
)z(H
0
2
0
+ω−
ω
=
Dùng b l c nàyộ ọ đ t oể ạ
tín hi u sin ệ2 kHz v i t n s l y m u ớ ầ ố ấ ẫ 8 kHz.
Khi tín hi u vào là xung dirac, tín hi u ra là: ệ ệ
)n(u)n
2
sin( π
)n(u)n
2
cos( π
)n
2
sin( π
)n
2
cos( π
Câu 5: Đ nh d ng d u ph y đ ng 16 bit g m 4ị ạ ấ ẩ ộ ồ
bit
ph n mũ theo sau là 12 bit ph n đ nh tr d ngầ ầ ị ị ạ
1.11. S hexa t ng đ ng v i s ố ươ ươ ớ ố 0.0259 là:
B6A0 B6A2 B6A3
B6A1
Câu 6: Bi u di n 1.15 có d u cho s ể ễ ấ ố - 0.5194
là:
7D83h BD83h BD84h
7D84h
Câu 7: Các c p ặc m bi n - tín hi uả ế ệ nào đúng
trong các c p sau:ặ
microphone - âm thanh, photodiode - ánh sáng,
thermocoupler - nhi t đệ ộ
microphone - nhi t đ , photodiode - ánh sáng,ệ ộ
thermocoupler - âm thanh
microphone - ánh sáng, photodiode - âm thanh,
thermocoupler - nhi t đ ệ ộ
microphone - âm thanh, photodiode - nhi t đ ,ệ ộ
thermocoupler - ánh sáng
Câu 8: Cho tín hi u ệ
)n(u)
2
n
sin()n(u2 π
+
đi
qua h th ng FIR ệ ố
)1n(x5.0)n(x)n(y −+=
.
Tín hi u ra t i ệ ạ n = 1 là:
0 4 2
1
Câu 9: Cho
1
z25.01
1
)z(X −
+
=
. Đây là bi nế
đ i Z c a hàm x(n) sau:ổ ủ
)n(u25.0 n
−
)n(u)25.0( n
−
-Trang 2
)n(u25.0 n
Không có k t qu nàoế ả
đúng
Câu 10: H sau: ệ
)2n(x)1n(y6.0)n(y −=−+
n đ nh Ổ ị Không nổ
đ nhị
n đ nh v i đi u ki n h nhân qu Ổ ị ớ ề ệ ệ ả
n đ nh v i đi u ki n h không nhân quỔ ị ớ ề ệ ệ ả
Câu 11: Tín hi u t ng t ệ ươ ự
)
2
t10.2(cos2)t(x
4
π
+=
đ c l y m u v i t n s ượ ấ ẫ ớ ầ ố 16 kHz và s hóa, sauố
đi vào b l c thông cao t n s c t ộ ọ ầ ố ắ
2/π
. Xem
b l c này là lý t ng. Tín hi u ra b l c sauộ ọ ưở ệ ộ ọ
khi đ c chuy n v l i t ng t là:ượ ể ề ạ ươ ự
không có tín hi u ệ v n là x(t)ẫ
x(t) v i biên đ g p đôiớ ộ ấ x(t) v i biên đ gi mớ ộ ả
m t n aộ ử
Câu 12: Tín hi u t ng t đ c l y m u v iệ ươ ự ượ ấ ẫ ớ
t n s 44.1 kHz r i tính DFT v i kích th c c aầ ố ồ ớ ướ ử
s DFT là 23.22 ms. Đ phân gi i c a DFTổ ộ ả ủ
(tính b ng Hz) là:ằ
40.07 43.07 42.07
41.07
Câu 13: Cho b l c FIR có ộ ọ
{ }
π−πππ−= ↑3/1,0,/1,2/1,/1,0,3/1)n(hd
Đáp ng biên đ t i ứ ộ ạ
π
π
=ω ,
2
,0
l n l t là:ầ ượ
0.076, 0.5 và 0.92 0.92, 0.5 và
0.076
0.076, 0.92 và 0.076 0.92, 0.076
và 0.92
Câu 14: B l c thông th p Butterworth có đ cộ ọ ấ ặ
đi m: ể
dB25lg20
;s/rad4.8152;s/rad9.10690
s
ps
−=δ
=Ω=Ω
Nên ch n b c c a bô ül c này là:ọ ậ ủ ọ
10 11 12
9
Câu 15: S có d u 8 bit ố ấ 1111 1111 có giá trị
th p phân t ng đ ng là:ậ ươ ươ
-1 1 -2
2
Câu 16: Dùng m t b x lý DSP 33MHz trongộ ộ ử
h th ng đ c l y m u v i t n s 25 kHz. N uệ ố ượ ấ ẫ ớ ầ ố ế
b x lý này có kh năng thi hành m t l nhộ ử ả ộ ệ
trong m t chu kỳ đ ng h thì s l nh thi hànhộ ồ ồ ố ệ
đ c trong m t m u là:ượ ộ ẫ
1.32 1320 825
825000
Câu 17: Tín hi u ệ
)n3(u)n(u −
là cách vi tế
khác c a tín hi u:ủ ệ
)3n()2n()1n()n( −δ+−δ+−δ+δ
)3n()1n()n( −δ+−δ+δ
)3n()2n()n( −δ+−δ+δ
)2n()1n()n( −δ+−δ+δ
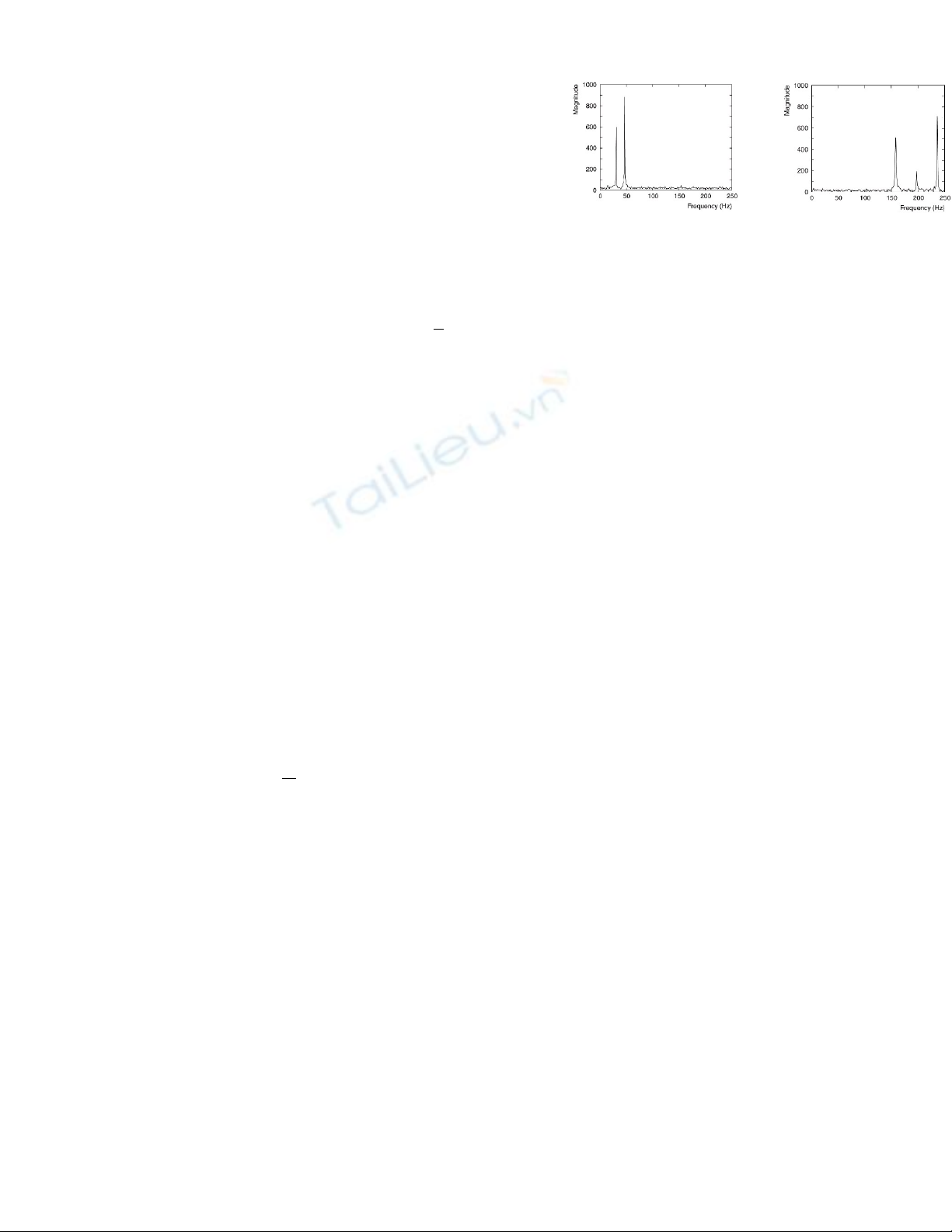
Câu 18: Cho ph biên đ c a hai tín hi u (xemổ ộ ủ ệ
hình bên)
T hình nh c a hai ph này, ta có th nói:ừ ả ủ ổ ể
(a) (b)
Không bi t đ c thông tin gì v tín hi uế ượ ề ệ
Tín hi u (a) bi n đ i ch m h n tín hi u (b)ệ ế ổ ậ ơ ệ
Tín hi u (b) bi n đ i ch m h n tín hi u (a)ệ ế ổ ậ ơ ệ
Tín hi u (b) bi n đ i nhanh h n tín hi u (a)ệ ế ổ ơ ệ
và c hai đ u là tín hi u tu n hoànả ề ệ ầ
Câu 19: Ba m u đ u tiên c a đáp ng xungẫ ầ ủ ứ
c a h nhân quủ ệ ả
)1n(x)n(x)1n(y4.0)n(y −−=−−
là:
0 , 0.6 , - 0.24 0 , 0.6 ,
0.24
1 , - 0.6 , - 0.24 1 , 0.6 ,
0.24
Câu 20: Cho hai h th ng:ệ ố
(1)
)2n(x5)1n(x3)n(x2)n(y −−−+=
(2)
)2n(x5)1n(x3)n(x2)n(y 222 −−−+=
-Trang 3
C hai h đ u tuy n tínhả ệ ề ế C hai h đ uả ệ ề
phi tuy nế
Ch có h (2) tuy n tính ỉ ệ ế Ch có h (1)ỉ ệ
tuy n tínhế
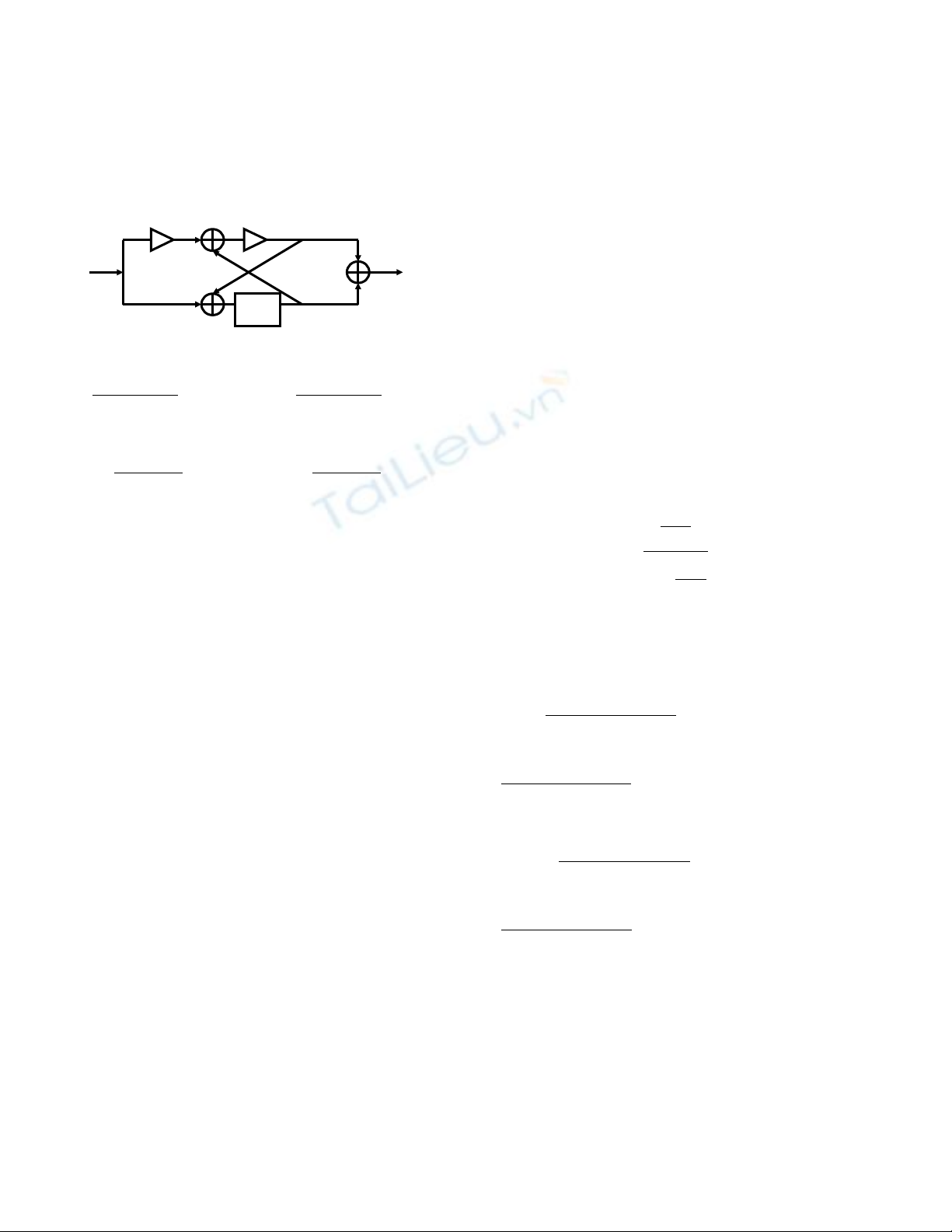
Câu 21: Cho h th ng:ệ ố
Hàm truy n đ t c a h này là:ề ạ ủ ệ
1
1
z1
aza
−
−
+
−−
1
1
z1
aza
−
−
+
+−
1
1
z1
aza
−
−
+
−
1
1
z1
aza
−
−
+
+
Câu 22: Cho hai tín hi uệ
{ }
0,0,0,0,1,1,1,1)n(x1↑
=
và
{ }
1,1,0,0,0,0,1,1)n(x2↑
=
. Quan h gi a ệ ữ X1(k)
và X2(k) là:
)k(X)j()k(X 2
k
1=
)k(X)j()k(X 2
k
1−=
)k(X)1()k(X
2
k
1
−=
)k(X)k(X 21 =
Câu 23: Cho
{ }
7,6,5,4,3,2,1,0)n(x ↑
=
.
T l u đ thu t toán FFT phân th i gian ừ ư ồ ậ ờ N = 8,
suy ra X(7) là:
)WWW1(4 3
8
2
88 ++−−
)WWW1(4 3
8
2
88 −−−−
)WWW1(4 3
8
2
88 +−−−
)WWW1(4 3
8
2
88 +++−
Câu 24: Tín hi u t ng t đ c l y m u v iệ ươ ự ượ ấ ẫ ớ
t n s ầ ố 16 kHz r i tính DFT ồ512 m u. T n sẫ ầ ố
(Hz) t i v ch ph ạ ạ ổ k = 127 là:
0 31.25 3968.75
127
Câu 25: B l c nhân quộ ọ ả:
y(n) - 0.2 y(n-1) = x(n) - x(n-2) có đáp ngứ
xung là:
)]2n(u)n(u[2.0
n
−−
)]2n(u)n(u[2.0
2n
−−
−
)]2n(u5)n(u[2.0
n
−−
)]2n(u25)n(u[2.0
n
−−
Câu 26: Cho b l c thông th p RC có hàmộ ọ ấ
truy n là:ề
RC
1
s
RC
1
)s(H
+
=
. Chuy n b l c nàyể ộ ọ
sang l c s v i t n s l y m u ọ ố ớ ầ ố ấ ẫ 1.5 kHz b ngằ
phép bi n đ i song tuy n, cho bi t ế ổ ế ế 1/RC =
2360.4. Hàm truy n c a l c s là:ề ủ ọ ố
1
1
z1193.01
)z1(4403.0
−
−
−
+
1
1
z1193.01
)z1(4403.0
−
−
−
−
1
1
z9975.01
)z1(9987.0
−
−
+
+
1
1
z9975.01
)z1(9987.0
−
−
+
−
Câu 27: L ng t hóa tín hi u t ng t có d iượ ử ệ ươ ự ả
biên đ t ộ ừ 0V đ n ế5V. Mu n l i l ng t hóaố ỗ ượ ử
không v t quá ượ 6x10-5 thì c n s bit ít nh t là:ầ ố ấ
8 16 17
15
Câu 28: Tai ng i có th nghe đ c âm thanhườ ể ượ
t 0 -22.05kHz. T n s l y m u nh nh t (kHz)ừ ầ ố ấ ẫ ỏ ấ
-1
a
z - 1
-Trang 4
cho phép khôi ph c hoàn toàn tín hi u âmụ ệ
thanh t các m u là:ừ ẫ
441 44.1 4.41
0.441
Câu 29: Cho hai h th ng:ệ ố
(1)
[ ]
)2n(x)1n(x)n(x
3
1
)n(y −+−+=
(2)
)1n(y2.0)n(x)n(y −+=
H (1) không đ quy, h (2) đ quyệ ệ ệ ệ
H (1) đ quy, h (2) không đ quy ệ ệ ệ ệ
C hai h đ u đ quy ả ệ ề ệ
C hai h đ u không đ quyả ệ ề ệ
Câu 30: Cho tín hi u ệ
)n(u
4
n
cos π
đi qua b l cộ ọ
có
đáp ng xung ứ
)2n(3)1n()n(2 −δ+−δ−δ
.
Tín hi u ra t i ệ ạ n = 1 là:
0
0.41
1 -
0.41
Câu 31: Cho
2
j
2j
j
e
2
1
1
e
)e(X
−
=ω−
ω−
ω
.
Đây là ph c a tín hi u sau:ổ ủ ệ
)1n(u
2
1
)1n(
2n
−
−
−
)2n(u
2
1
)1n(
2n
−
−
−
C ả và đ u đúng ề C ả và
đ u saiề
Câu 32: Cho
{ }
3,2,1,0)n(x 4↑
=
và các quan
h sau:ệ
})n(y{DFT)k(X)k(Y};)n(x{DFT)k(X
4
2
4
===
Tín hi u ệ
4
)n(y
là:
}8,6,8,14{ ↑
}4,10,12,10{ ↑
}8,6,8,10{ ↑
}10,12,8,4{↑
Câu 33: Đ tìm ểx(n) t ừX(z), ng i ta dùng cácườ
l nh Matlab sau:ệ
>> b = 1 ; a = poly ([0.9, 0.9, -0.9]) ;
>> [r, p, c] = residuez (b, a)
Các l nh trên đ c áp d ng cho ệ ượ ụ X(z) là:
)z9.01)(z9.01)(z9.01()z(X
111 −−−
−−+=
)z9.01)(z9.01)(z9.01()z(X
111 −−−
−++=
)z9.01)(z9.01)(z9.01(
1
)z(X
111 −−−
−++
=
)z9.01)(z9.01)(z9.01(
1
)z(X
111 −−−
−−+
=
Câu 34: Đo n l nh Matlab sau:ạ ệ
>> n = [0:1:3]; k = [0:1:3]; X1 = [5 2 -2 4];
>> W = exp(-j*2*pi/4); nk = n'*k;
>> Wnk = W.^(nk); X2 = X1 * Wnk
dùng đ tính:ể
DFT{ x(n) } DFT -1
{X(k)}
DFT{ x(n) } v i ớ
{ }
4,2,2,5)n(x −= ↑
DFT -1 {X(k)} v i ớ
{ }
4,2,2,5)k(X −= ↑
Câu 35: Mu n thi t k b l c FIR thông d i cóố ế ế ộ ọ ả
t n s gi i h n d i thông là 3.5 kHz và 4.5 kHz,ầ ố ớ ạ ả
b r ng d i chuy n ti p 500Hz, suy hao d iề ộ ả ể ế ả
ch n 50 dB, ta nên ch n c a s :ắ ọ ử ổ
Ch nh tữ ậ Hanning Hamming
Blackman
Câu 36: Thi t k b l c FIR thông th p có t nế ế ộ ọ ấ ầ
s gi i h n d i thông và d i ch n là 10 kHz vàố ớ ạ ả ả ắ
22.5 kHz, t n s l y m u là 50kHz b ng c aầ ố ấ ẫ ằ ử
s Blackman. Nên ch n chi u dài c a s là:ổ ọ ề ử ổ
-Trang 5
23 24 25
26
Câu 37: D i đ ng c a m t b A/D là 60.2 dB.ả ộ ủ ộ ộ
Đó là b A/D:ộ
8 bit 16 bit 10 bit
32 bit
Câu 38: Tín hi uệ
)1n()n3(u2n−δ−
chính là:
{ }
0,0,2,0 ↑
{ }
0,0,2,0 ↑
{ }
↑
0,0,2,0
{ }
0,0,2,0
↑
Câu 39: Cho tín hi u:ệ
)1n(u)6.0(
12
25
4
5
)1n(
6
5
)n(x 1n −
−+−δ= −
Bi n đ i Z c a x(n) là:ế ổ ủ
)6.0z)(1z(z
5.0
−−
)6.0z(z
5.0
−
)1z(z
5.0
−
)6.0z)(1z(
5.0
−−
Câu 40: H th ng có hàm truy n đ t: ệ ố ề ạ
)1z4)(1z2(
z
)z(H −−
=
có ph ng trình sai phân là:ươ
)1n(x25.0)2n(y25.0)1n(y75.0)n(y
−=−+−−
)1n(x125.0)2n(y25.0)1n(y75.0)n(y
−=−+−−
)1n(x125.0)2n(y125.0)1n(y75.0)n(y
−=−+−−
)1n(x25.0)2n(y25.0)1n(y25.0)n(y
−=−+−−
H TẾ
Khoa Đi n t - Vi nệ ử ễ
thông