PHÒNG GD&ĐT QUỐC OAI
ĐỀ OLYMPIC TOÁN 8
Năm học 2023 - 2024
Thời gian: 120 phút (không kể thời gian giao đề)
Họ và tên: ……………….....................………..……..…SBD:.............…
Câu 1 (4 điểm)
1/ Cho
x2 3= −
. Tính
2
x 4x 3
3−+
2/ Cho x, y là 2 số khác nhau thoả mãn: x2 + y = y2 + x.
Tính giá trị của biểu thức
22
x y xy
Axy 1
++
=−
3/ Cho
33
x 2025 2023= −
. Tính
x2
6
−
Câu 2 (4 điểm)
1/ Rút gọn biểu thức
22 2
x 5 x 2x 5 2x
A:
x 25 x 5x 2x 10 5 x
−−
=++
− + +−
, với
5
x 0; x 5; 2
x≠ ≠± ≠
.
2/ Cho
a,b
, c thỏa mãn:
2
(3a 2b) | 4b 3c| 0− + −≤
Tính giá trị của biểu thức
3 33
abc
Qabc
++
=
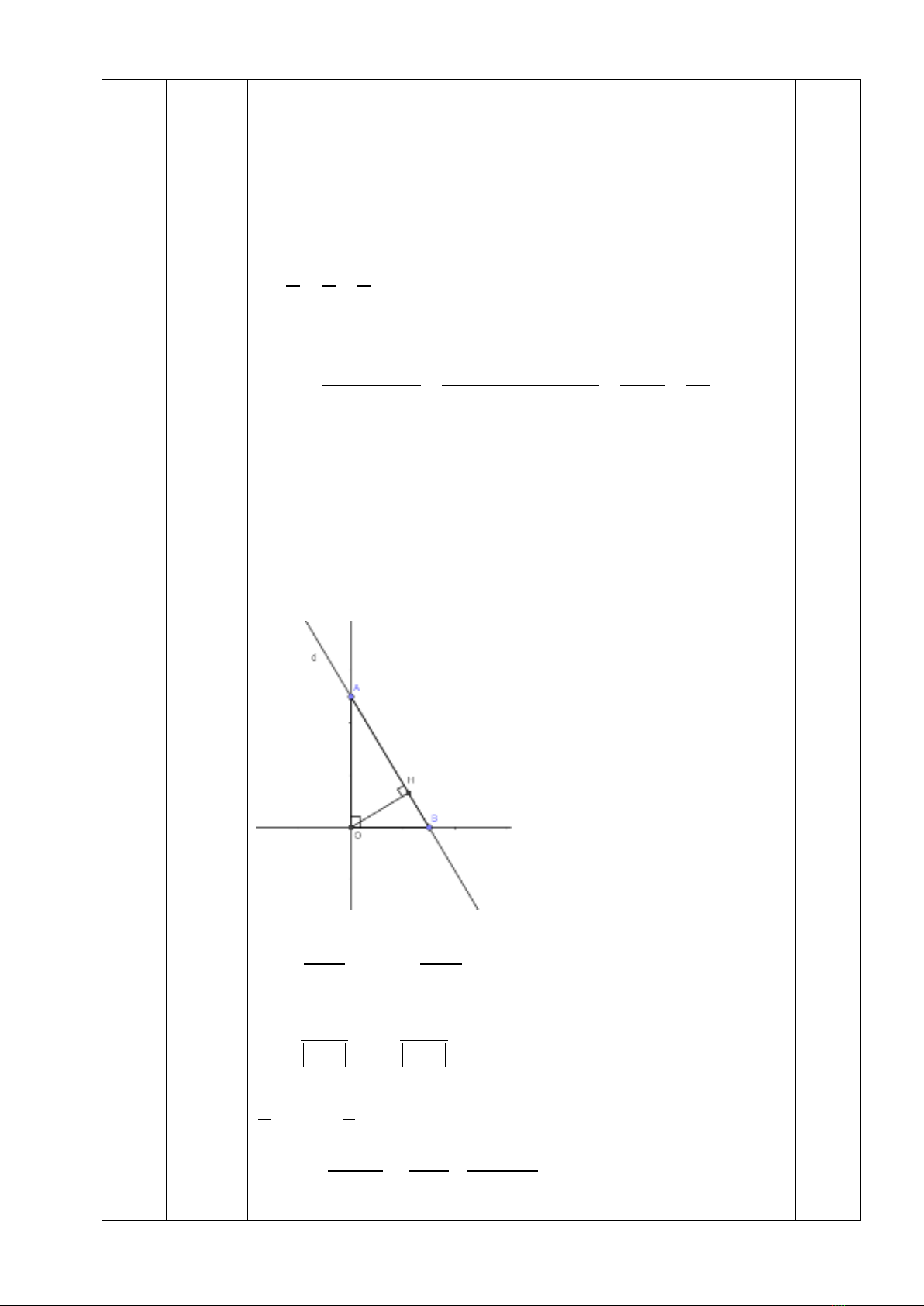
3/ Trong mặt phẳng Oxy, cho đường thẳng (d):
( 4) ( 3) 1m xm y− +− =
(m là tham
số). Tìm m để khoảng cách từ gốc tọa độ đến đường thẳng (d) là lớn nhất.
Câu 3 (4 điểm)
1/ Trong túi đựng 48 viên bi cùng kích thước và khối lượng với hai màu đỏ và
xanh. Lấy ngẫu nhiên một viên bi từ túi. Biết rằng xác suất lấy được viên bi đỏ bằng
92% xác suất lấy được viên bi màu xanh. Hỏi trong túi có bao nhiêu viên bi màu đỏ,
bao nhiêu viên bi màu xanh?
2/ Giải phương trình:
22
1 11
.
2 3 ( 1) 48xx x
= +
+− +
3/ Cho đa thức A(x) = ax3 + bx2 + cx + d với a là số nguyên dương. Biết rằng:
A(5) – A(4) = 2024.
Chứng minh: A(7) – A(2) chia hết cho 5
Câu 4 (6 điểm)
Cho ∆ABC cân tại A. Trên AB, AC lần lượt lấy D, E sao cho AD = AE.
a/ Tứ giác BDEC là hình gì?
(Đề gồm có 02 trang)
ĐỀ CHÍNH THỨC