B GIÁO D C VÀ ĐÀO T OỘ Ụ Ạ
________________
Đ THI ỀCHÍNH TH CỨ
K THI THPT QU C GIA NĂM 2019Ỳ Ố
Bài thi: TOÁN H CỌ
Th i gian làm bài: ờ90 phút, không k th i gian phát để ờ ề
Mã đ 104ề
Câu 1. S cách ch n 2 h c sinh t 8 h c sinh làố ọ ọ ừ ọ
A.
2
8
C
. B.
2
8
. C.
2
8
A
. D.
8
2
.
Câu 2. Trong không gian
Oxyz
, cho m t ph ngặ ẳ
( )
: 4 3 1 0P x y z+ + − =
. Vect nào d i đây là m tơ ướ ộ
vect pháp tuy n c a ơ ế ủ
( )
P
?
A.
4
(3;1; 1)n= −
r
. B.
3
(4;3;1)n=
r
. C.
2
(4;1; 1)n= −
r
. D.
1
(4;3; 1)n= −
r
.
Câu 3. Nghi m c a ph ng trình ệ ủ ươ
2 1
2 32
−
=
x
là
A.
3x=
. B.
17
2
x=
. C.
5
2
x
=
. D.
2x
=
.
Câu 4. Th tích c a kh i lăng tr có di n tích đáy ể ủ ố ụ ệ
B
và chi u cao ề
h
là
A.
4
3Bh
. B.
1
3Bh
. C.
3Bh
. D.
Bh
.
Câu 5. S ph c liên h p c a s ph c ố ứ ợ ủ ố ứ
3 2i
−
là
A.
3 2i
− +
. B.
3 2i
+
. C.
3 2i
− −
. D.
2 3i
− +
.
Câu 6. Trong không gian
Oxyz
, hình chi u vuông góc c a đi m ế ủ ể
(3;1; 1)M
−
trên tr c ụ
Oy
có t a đ làọ ộ
A.
(0;1;0)
. B.
(3;0;0)
. C.
(0;0; 1)
−
. D.
(3;0; 1)
−
.
Câu 7. Cho c p s c ng ấ ố ộ
( )
n
u
v i ớ
1
1u
=
và
2
4u
=
. Công sai c a c p s c ng đã cho b ngủ ấ ố ộ ằ
A.
5
. B.
4
. C.
3
−
. D.
3
.
Câu 8. H t t c các nguyên hàm c a hàm s ọ ấ ả ủ ố
( )
2 4f x x
= +
là
A.
2
2 4x x C
+ +
. B.
2
4x x C
+ +
. C.
2
x C
+
. D.
2
2x C
+
.
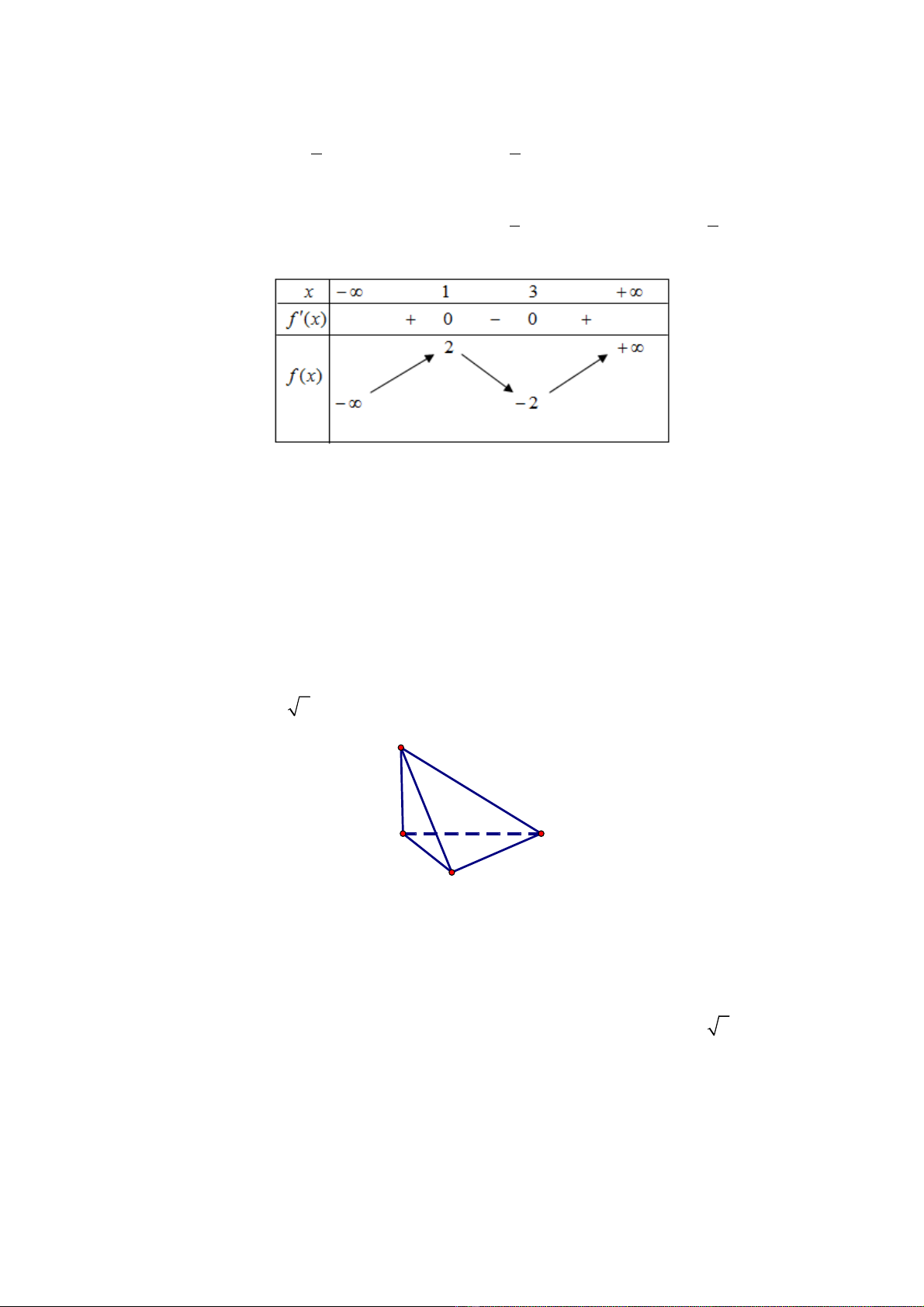
Câu 9. Đô thi cua ham sô nao d i đây co dang nh đng cong trong hinh ve bên? ươ ư ươ
A.
3
2 3 1y x x
= − +
. B.
4 2
2 4 1y x x
= − + +
. C.
4 2
2 4 1y x x
= − +
. D.
3
2 3 1y x x
= − + +
.
Câu 10. Cho ham sô
( )
f x
co bang biên thiên nh sau: ư
Ham sô đa cho nghich biên trên khoang nao d i đây? ươ
A.
( )
0;1
. B.
( )
1;
+
. C.
( )
1;0
−
. D.
( )
0;
+
.
Câu 11. Trong không gian
Oxyz
, cho đng th ng ườ ẳ
3 1 5
:1 2 3
x y z
d
− + −
= =
−
. Vect nào d i đây là m tơ ướ ộ
vec t ch ph ng c a ơ ỉ ươ ủ
d
.
A.
( )
1
3; 1;5u
= −
ur
. B.
( )
3
2;6; 4u
= −
uur
. C.
( )
4
2; 4;6u= − −
uur
. D.
( )
2
1; 2;3u= −
uur
.
Câu 12. V i ớ
a
là s th c d ng tùy ý, ố ự ươ
2
3
log a
b ng?ằ
A.
3
2log a
. B.
3
1log
2a
+
. C.
3
1log
2a
. D.
3
2 log a+
.
Câu 13. Th tích kh i nón có chi u cao ể ố ề
h
và bán kính đáy
r
là
A.
2
2
π
r h
. B.
2
π
r h
. C.
2
1
3
π
r h
. D.
2
4
3
π
r h
.
Câu 14. Cho hàm số
( )f x
có b ng bi n thiên nh sau:ả ế ư
Hàm s đã cho đt c c ti u t iố ạ ự ể ạ
A.
2
= −
x
. B.
1
=
x
. C.
3
=
x
. D.
2
=
x
.
Câu 15. Bi t ế
1 1
0 0
( ) 2; ( ) 4f x dx g x dx= = −
� �
. Khi đó
[ ]
1
0
( ) ( )f x g x dx+
b ngằ
A. 6. B. -6. C.
2
−
. D.
2
.
Câu 16. Cho hai s ph c ố ứ
1 2
2 , 1z i z i= − = +
. Trên m t ph ng t a đ ặ ẳ ọ ộ Oxy, đi m bi u di n s ph cể ể ễ ố ứ
1 2
2z z+
có t a đ là:ọ ộ
A.
( )
5; 1
−
. B.
( )
1;5
−
. C.
( )
5;0
. D.
( )
0;5
.
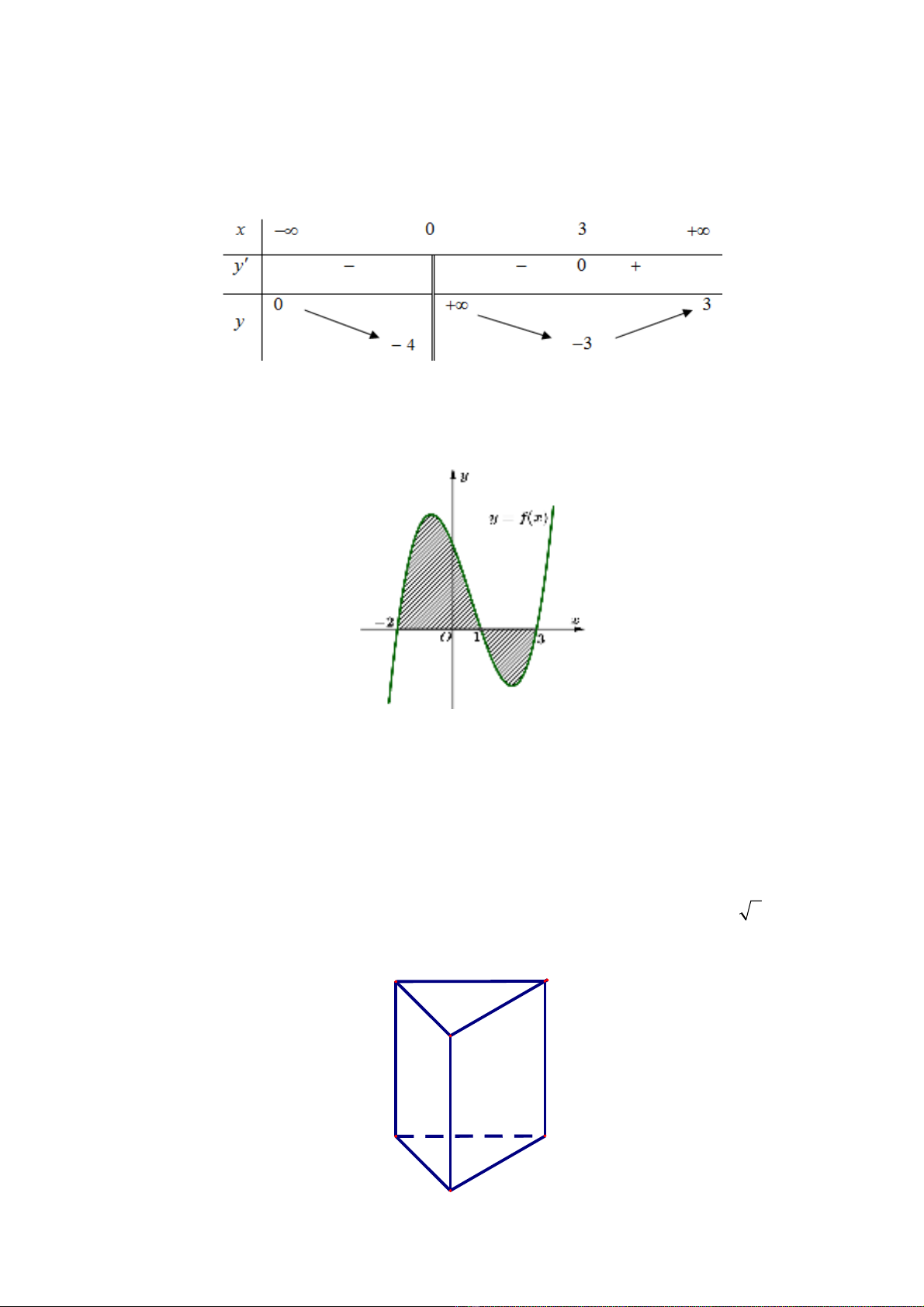
Câu 17. Cho hình chóp
.S ABC
có
SA
vuông góc v i m t ph ng ớ ặ ẳ
( )
ABC
,
2SA a
=
, tam giác
ABC
vuông cân t i ạ
B
và
2AB a
=
.(minh h a nh hình v bên)ọ ư ẽ .
A
C
B
S
Góc gi a đng th ng ữ ườ ẳ
SC
và m t ph ng ặ ẳ
( )
ABC
b ngằ
A.
60
. B.
45
. C.
30
. D.
90
.
Câu 18. Trong không gian
Oxyz
, cho m t c u ặ ầ
( )
2 2 2
: 2 2 7 0S x y z y z
+ + − + − =
. Bán kính c a m t c uủ ặ ầ
đã cho b ngằ
A.
9
. B.
3
. C.
15
. D.
7
.
Câu 19. Trong không gian
Oxyz
, cho hai đi m ể
( )
4;0;1A
,
( )
2; 2;3B
−
. M t ph ng trung tr c c a đo nặ ẳ ự ủ ạ
th ng ẳ
AB
có ph ng trình làươ
A.
6 2 2 1 0x y z
− − − =
. B.
3 6 0x y z
+ + − =
. C.
2 6 0x y z
+ + − =
. D.
3 0x y z
− − =
.
Câu 20. G i ọ
1 2
,z z
là hai nghi m ph c c a ph ng trình ệ ứ ủ ươ
2
4 7 0z z
− + =
. Giá tr c a ị ủ
2 2
1 2
z z
+
b ngằ
A. 10. B. 8. C. 16. D. 2.
Câu 21. Giá tr nh nh t c a hàm s ị ỏ ấ ủ ố
( )
3
3f x x x
= −
trên đo n ạ
[ ]
3;3
−
b ngằ
A.
18
. B.
18
−
. C.
2
−
. D.
2
.
Câu 22. M t c s s n xu t c hai b n c hình tr có chi u cao b ng nhau, bán kính đáy l n l tộ ơ ở ả ấ ố ể ướ ụ ề ằ ầ ượ
b ng ằ
1m
và
1,5m
. Ch c s d đnh làm m t b n c m i, hình tr , có cùng chi u cao và có thủ ơ ở ự ị ộ ể ướ ớ ụ ề ể
tích b ng t ng th tích c a hai b trên. Bán kính đáy c a b n c d đnh làm ằ ổ ể ủ ể ủ ể ướ ự ị g n nh tầ ấ v i k tớ ế
qu nào d i đây?ả ướ
A.
1, 6m
. B.
2,5m
. C.
1,8m
. D.
2,1m
.
Câu 23. Cho hàm s ố
( )
y f x
=
có b ng bi n thiên nh sau:ả ế ư
T ng s ti m c n đng và ti m c n ngang c a đ th hàm s đã cho làổ ố ệ ậ ứ ệ ậ ủ ồ ị ố
A.
2
. B.
1
. C.
3
. D.
4
.
Câu 24. Cho hàm s ố
( )
f x
liên t c trên ụ
R
. G i ọ
S
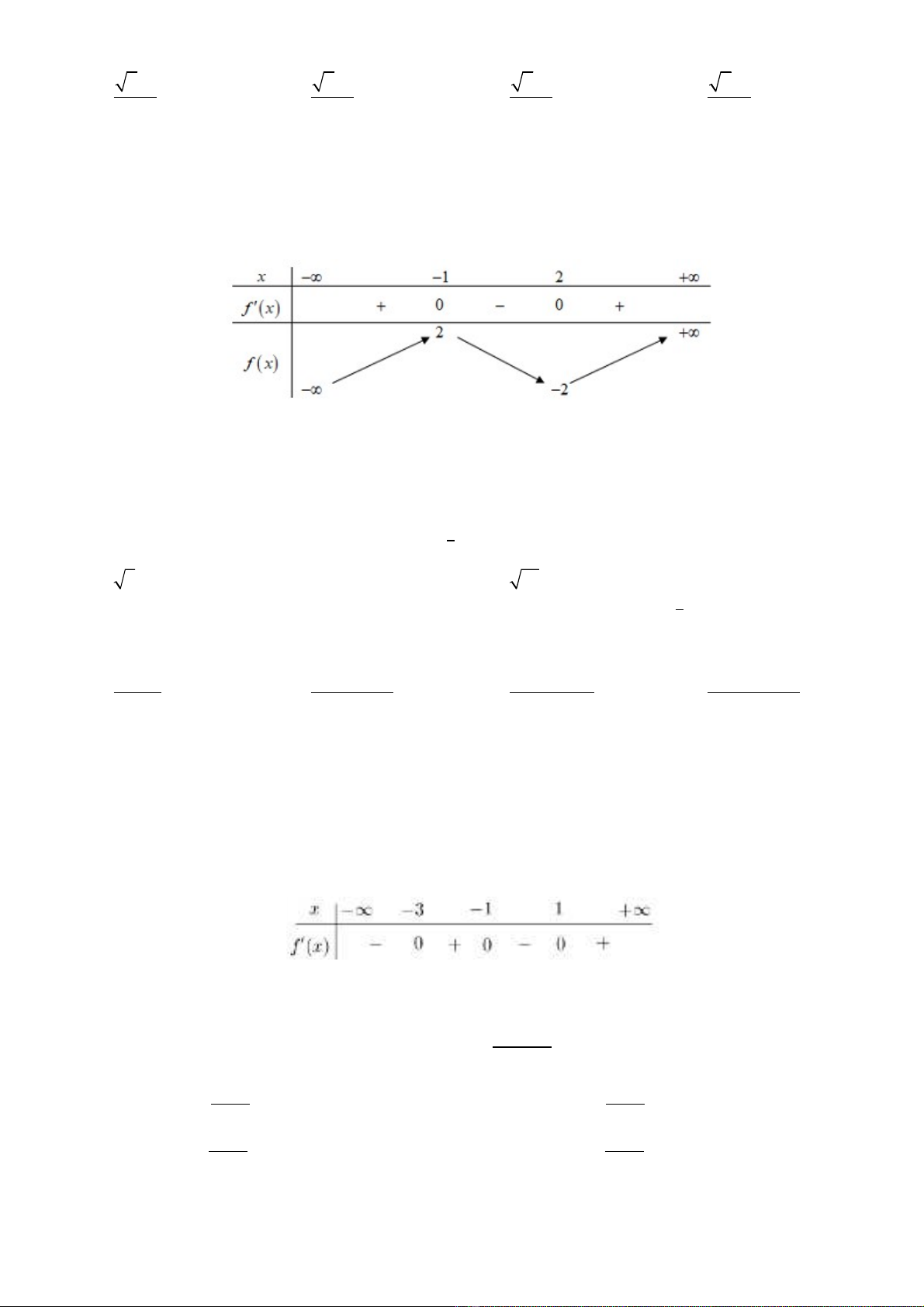
là di n tích hình ph ng gi i h n b i các đngệ ẳ ớ ạ ở ườ
( )
, 0, 2y f x y x
= = = −
và
3x
=
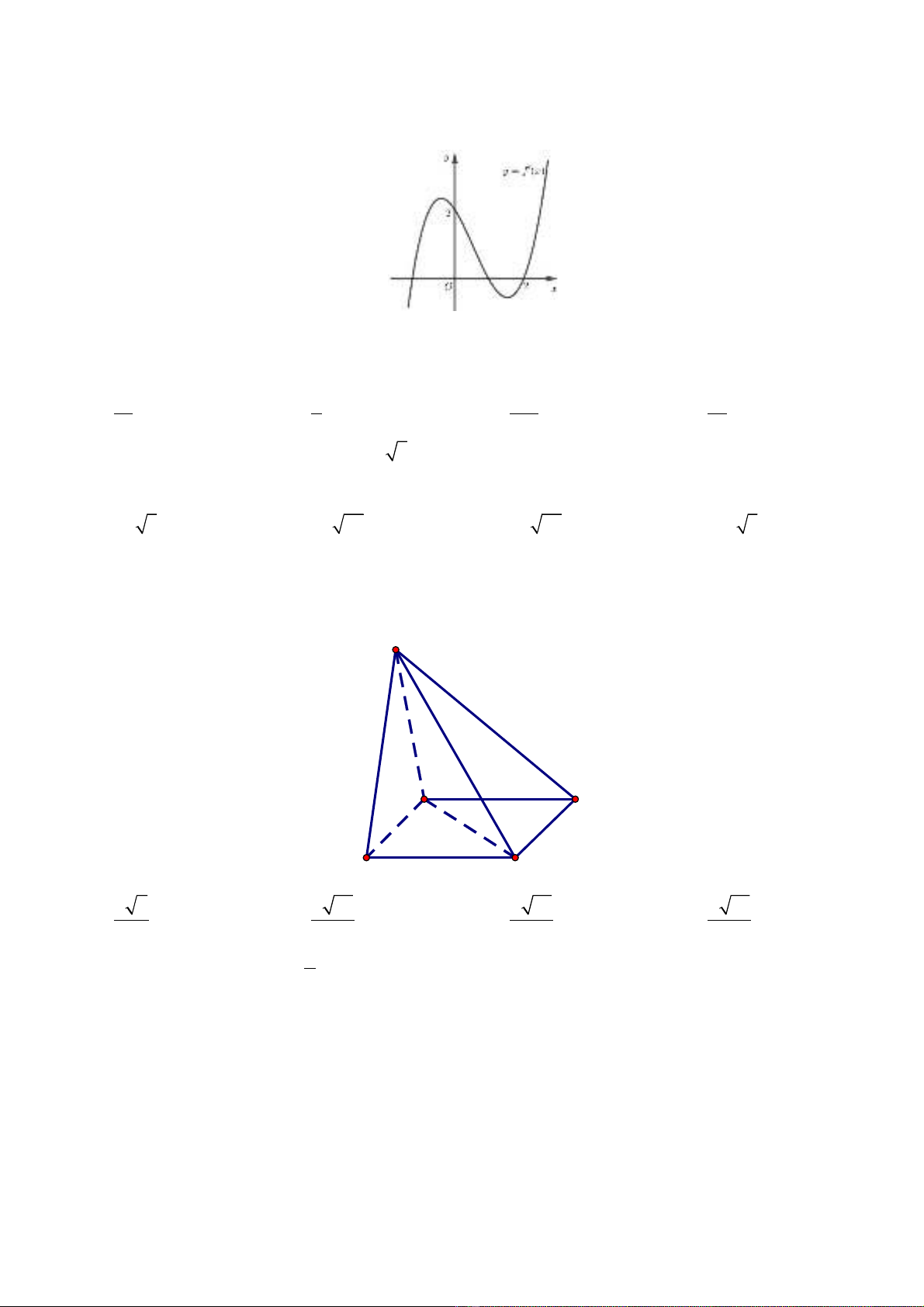
(nh hình v bên). M nh đ nào d i đây là đúng?ư ẽ ệ ề ướ
A.
( ) ( )
1 3
2 1
S f x dx f x dx
−
= −
� �
. B.
( ) ( )
1 3
2 1
S f x dx f x dx
−
= − +
� �
.
C.
( ) ( )
1 3
2 1
S f x dx f x dx
−
= +
� �
. D.
( ) ( )
1 3
2 1
S f x dx f x dx
−
= − −
� �
.
Câu 25. Hàm s ố
2
3
x x
y
−
=
có đo hàm làạ
A.
2
3 .ln 3
x x
−
. B.
( )
2
2 1 3
x x
x
−
−
. C.
( )
2
2 1
.3
x x
x x
− −
−
. D.
( )
2
2 1 3 .ln 3
x x
x
−
−
.
Câu 26. Cho kh i lăng tr đng ố ụ ứ
.ABC A B C
có đáy là tam giác đu c nh ề ạ
a
và
2AA a
=
(minh h aọ
nh hình v bên). Th tích c a kh i lăng tr đã cho b ngư ẽ ể ủ ố ụ ằ
C
B
A
B'
C'
A'
A.
3
6
4
a
. B.
3
6
6
a
. C.
3
6
12
a
. D.
3
6
2
a
.
Câu 27. Nghi m c a ph ng trình ệ ủ ươ
( ) ( )
3 3
log 2 1 1 log 1x x
+ = + −
là
A.
4x
=
. B.
2x
= −
. C.
1x
=
. D.
2x
=
.
Câu 28. Cho
,a b
là hai s th c d ng th a mãn ố ự ươ ỏ
3
8ab
=
. Giá tr c a ị ủ
2 2
log 3loga b
+
b ngằ
A.
8
. B.
6
. C.
2
. D.
3
.
Câu 29. Cho hàm s ố
( )
f x
có b ng bi n thiên nh sau:ả ế ư
S nghi m c a ph ng trình ố ệ ủ ươ
( )
2 3 0f x + =
là
A.
3
. B.
1
. C.
2
. D.
0
.
Câu 30. Cho hàm s ố
( )
f x
có đo hàm ạ
( ) ( )
2
1 ,f x x x x
= + ∀ ᄀ
. S đi m c c tr c a hàm s đã choố ể ự ị ủ ố
là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 31. Cho s ph c ố ứ
z
th a ỏ
(2 ) 3 16 2( )i z i z i
− + + = +
. Môđun c a ủ
z
b ngằ
A.
5
. B.
13
. C.
13
. D.
5
.
Câu 32. Cho hàm s ố
( )f x
. Bi t ế
(0) 4f
=
và
2
'( ) 2sin 3, ᄀf x x x= + ∀
, khi đó
4
0
( )f x dx
π
b ngằ
A.
2
2
8
π
−
. B.
2
8 8
8
π π
+ −
. C.
2
8 2
8
π π
+ −
. D.
2
3 2 3
8
π π
+ −
.
Câu 33. Trong không gian
Oxyz
, cho các đi m ể
( )
2; 1;0A−
,
( )
1; 2;1B
,
( )
3; 2;0C
−
và
( )
1;1; 3D
−
.
Đng th ng đi qua ườ ẳ
D
và vuông góc v i m t ph ng ớ ặ ẳ
( )
ABC
có ph ng trình làươ
A.
1 2
x t
y t
z t
=
=
= − −
. B.
1 2
x t
y t
z t
=
=
= −
. C.
1
1
2 3
x t
y t
z t
= +
= +
= − −
. D.
1
1
3 2
x t
y t
z t
= +
= +
= − +
.
Câu 34. Cho hàm s ố
( )
f x
, có b ng xét d u ả ấ
( )
f x
nh sau:ư
Hàm s ố
( )
5 2y f x
= −
đng bi n trên kho ng nào d i đây?ồ ế ả ướ
A.
( )
; 3
− −
. B.
( )
4;5
. C.
( )
3; 4
. D.
( )
1;3
.
Câu 35. H t t c các nguyên hàm c a hàm s ọ ấ ả ủ ố
( ) ( )
2
3 2
2
x
f x
x
-
=-
trên kho ng ả
( )
2;+ᄀ
là
A.
( )
4
3ln 2 2
x C
x
- + +
-
. B.
( )
2
3ln 2 2
x C
x
- + +
-
.
C.
( )
2
3ln 2 2
x C
x
- - +
-
. D.
( )
4
3ln 2 2
x C
x
- - +
-
.
Câu 36. Cho ph ng trình ươ
( )
2
9 3 3
log log 4 1 logx x m
− − = −
(
m
là tham s th c). Có t t c bao nhiêuố ự ấ ả
giá tr nguyên c a ị ủ
m
đ ph ng trình đã cho có nghi m?ể ươ ệ
A.
5
. B.
3
. C. Vô số. D.
4
.
Câu 37. Cho hàm s ố
( )
f x
, hàm s ố
( )
y f x
=
liên t c trên ụ
R
và có đ th nh hình v bên. B tồ ị ư ẽ ấ
ph ng trình ươ
( )
2f x x m
> +
(
m
là tham s th c) nghi m đúng v i m i ố ự ệ ớ ọ
( )
0;2x
khi và ch khiỉ
A.
( )
2 4m f
−
. B.
( )
0m f
. C.
( )
0m f
<
. D.
( )
2 4m f
< −
. .
Câu 38. Ch n ng u nhiên hai s khác nhau t 23 s nguyên d ng đu tiên. Xác su t đ ch n đcọ ẫ ố ừ ố ươ ầ ấ ể ọ ượ
hai s có t ng là m t s ch n b ngố ổ ộ ố ẵ ằ
A.
11
23
. B.
1
2
. C.
265
529
. D.
12
23
.
Câu 39. Cho hình tr có chi u cao b ngụ ề ằ
3 3
. C t hình tr đã cho b i m t ph ng song song v i tr c vàắ ụ ở ặ ẳ ớ ụ
cách tr c m t kho ng b ng 1, thi t di n thu đc có di n tích b ng 18. Di n tích xung quanh c aụ ộ ả ằ ế ệ ượ ệ ằ ệ ủ
hình tr đã cho b ngụ ằ
A.
6 3
π
. B.
6 39
π
. C.
3 39
π
. D.
12 3
π
.
Câu 40. Cho hình chóp
.S ABCD
có đáy là hình vuông c nh ạ
a
, m t bênặ
SAB
là tam giác đu và n mề ằ
trong m t ph ng vuông góc v i m t ph ng đáy (minh h a nh hình v bên). Kho ng cách t ặ ẳ ớ ặ ẳ ọ ư ẽ ả ừ
B
đn m t ph ngế ặ ẳ
( )
SAC
b ngằ
A
B
D
C
S
A.
2
2
a
. B.
21
28
a
. C.
21
7
a
. D.
21
14
a
.
Câu 41. Cho đng thăng ươ
3
2
y x
=
va parabol
2
y x a= +
(
a
la tham sô th c d ng). Goi ư ươ
1
S
va
2
S
lân
l t la diên tich cua 2 hinh phăng đc gach cheo trong hinh ve bên. Khi ươ ươ
1 2
S S=
thi
a
thuôc khoang
nao sau đây





















![Đề thi tiếng Anh tốt nghiệp THPT 2025 (Chính thức) kèm đáp án [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250627/laphong0906/135x160/9121751018473.jpg)




