http://ductam_tp.violet.vn/ ĐỀ THI THỬ ĐH&CĐ LÀNI NĂM HỌC 2010-2011
TRƯỜNG THPT NGUYỄN TRUNG THIÊN MÔN TOÁN-KHỐI A+B: (180 phút)
-----------------------@--------------------------- --------------------------------------@-----------------------------------
(Không kể thời gian phát đề)
A.PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7 điểm):
Câu I (2 điểm): Cho hàm số 3 2 2 3
3 3( 1)
y x mx m x m m
(1)
1.Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) ứng với m=1
2.Tìm m để hàm số (1) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến
góc tọa độ O bằng 2lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến góc tọa độ O.
Câu II (2 điểm):
1. Giải phương trình : 2
2 os3x.cosx+ 3(1 sin2x)=2 3 os (2 )
4
c c x
2. Giải phương trình :
2 2
1 2 2 1 2 2 2
2
log (5 2 ) log (5 2 ).log (5 2 ) log (2 5) log (2 1).log
(5 2 )
x
x x x x x x
Câu III (1 điểm): Tính tích phân : 6
0
tan( )
4
os2x
x
c
Câu IV (1 điểm): Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với đáy
và SA=a .Gọi M,N lần lượt là trung điểm của SB và SD;I là giao điểm của SD và mặt phẳng
(AMN). Chứng minh SD vuông góc với AI và tính thể tích khối chóp MBAI.
Câu V (1 điểm): Cho x,y,z là ba số thực dương có tổng bằng 3.Tìm giá trị nhỏ nhất của biểu thức
2 2 2
3( ) 2
P x y z xyz
.
B. PHẦN TỰ CHỌN (3 điểm): Thí sinh chỉ được chọn một trong hai phàn (phần 1 hoặc 2)
1.Theo chương trình chuẩn:
Câu VIa (2 điểm):
1. Trong mặt phẳng với hệ toạ đ ộ Oxy cho điểm C(2;-5 ) và đường thẳng
:3 4 4 0
x y
.
Tìm trên
hai điểm A và B đối xứng nhau qua I(2;5/2) sao cho diện tích tam giác ABC
bằng15.
2. Trong không gian với hệ toạ độ Oxyz cho mặt cầu 2 2 2
( ): 2 6 4 2 0
S x y z x y z
.
Viết phương trình mặt phẳng (P) song song với giá của véc tơ
(1;6;2)
v
, vuông góc với mặt
phẳng
( ): 4 11 0
x y z
và tiếp xúc với (S).
Câu VIIa(1 điểm): Tìm hệ số của
4
x
trong khai triển Niutơn của biểu thức :
2 10
(1 2 3 )
P x x
2.Theo chương trình nâng cao:
Câu VIb (2 điểm):
1.Trong mặt phẳng với hệ toạ độ Oxy cho elíp 2 2
( ): 1
9 4
x y
E
và hai điểm A(3;-2) , B(-3;2) .
Tìm trên (E) điểm C có hoành độ và tung độ dương sao cho tam giác ABC có diện tích lớn nhất.
2.Trong không gian với hệ toạ độ Oxyz cho mặt cầu 2 2 2
( ): 2 6 4 2 0
S x y z x y z
.
Viết phương trình mặt phẳng (P) song song với giá của véc tơ
(1;6;2)
v
, vuông góc với mặt
phẳng
( ): 4 11 0
x y z
và tiếp xúc với (S).
Câu VIIb (1 điểm):
Tìm số nguyên dương n sao cho thoả mãn 2
0 1 2
2 2 2 121
...
2 3 1 1
nn
n n n n
C C C C
n n
-------------------------------------------------------HẾT--------------------------------------------------------
Cán bộ coi thi không g ải thích gì thêm
Họ tên thí sinh:.................................................... Số báo danh:..............................
ĐÁP ÁN VÀ
THANG ĐIỂM
Câu NỘI DUNG Điêm
2. Ta có , 2 2
3 6 3( 1)
y x mx m
Để hàm số có cực trị thì PT ,
0
y
có 2 nghiệm phân biệt
2 2
2 1 0
x mx m
có 2 nhiệm phân
biệt
1 0,
m
05
Cực đại của đồ thị hàm số là A(m-1;2-2m) và cực tiểu của đồ thị hàm số
là
B(m+1;-2-2m)
025
Theo giả thiết ta có 2
3 2 2
2 6 1 0
3 2 2
m
OA OB m m m
Vậy có 2 giá trị của m là
3 2 2
m và
3 2 2
m .
025
1.
os4x+cos2x+ 3(1 sin 2 ) 3 1 os(4x+ )
2
os4x+ 3sin4 os2x+ 3sin2 0
PT c x c
c x c x
05
sin(4 ) sin(2 ) 0
6 6
18 3
2sin(3 ). osx=0
6x= 2
x x
x k
x c
k
Vậy PT có hai nghiệm
2
x k
và
18 3
x k
.
05
2. ĐK :
1 5
2 2
0
x
x
.
Với ĐK trên PT đã cho tương đương với
2
22
2 2 2 2
2
log (5 2 )
log (5 2 ) 2log (5 2 ) 2log (5 2 )log (2 1)
log (2 1)
x
x x x x
x
05
2
2 2
2
1
4
log (2 1) 1 1
log (5 2 ) 2log (2 1) 2
2
log (5 2 ) 0 2
x
x
x x x x
xx
025
I
II
Kết hợp với ĐK trên PT đã cho có 3 nghiệm x=-1/4 , x=1/2 và x=2.
025
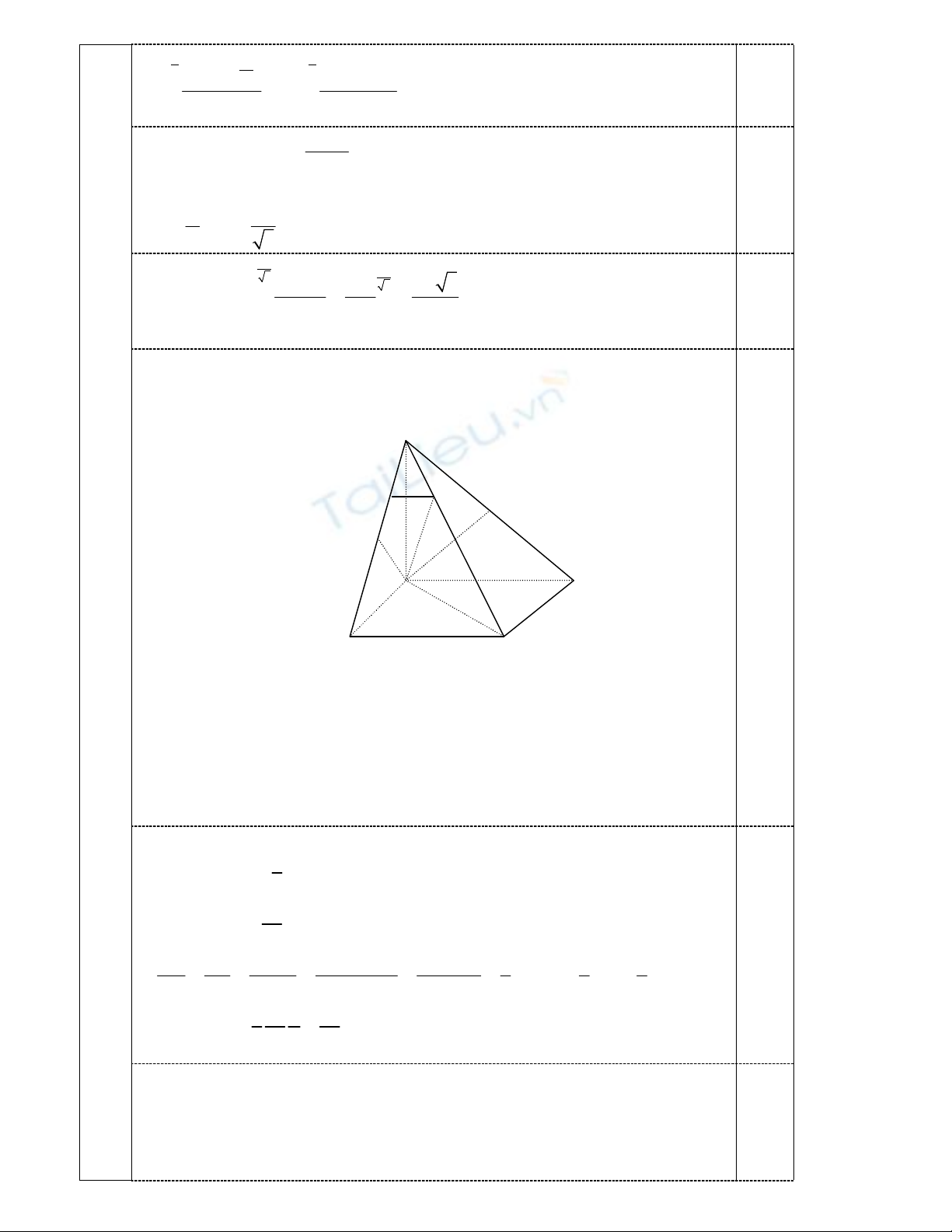
26 6
2
0 0
tan( ) tan 1
4
os2x (tanx+1)
xx
I dx dx
c
025
Đặt 2
2
1
tanx dt= (tan 1)
cos
t dx x dx
x
0 0
1
6
3
x t
x t
05
Suy ra
11
33
20
0
1 1 3
( 1) 1 2
dt
It t
.
025
Ta có
,( , )
,( )
AM BC BC SA BC AB
AM SB SA AB
AM SC
(1)
Tương tự ta có
AN SC
(2)
Từ (1) và (2) suy ra
AI SC
05
Vẽ IH song song với BC cắt SB tại H. Khi đó IH vuông góc với (AMB)
Suy ra 1
.
3
ABMI ABM
Ta có
2
4
ABM
a
S
2 2
2 2 2 2 2
. 1 1 1
2 3 3 3
IH SI SI SC SA a
IH BC a
BC SC SC SA AC a a
Vậy
2 3
1
3 4 3 36
ABMI
a a a
V
05
III
IV
V
Ta c ó:
2
3 ( ) 2( ) 2
3 9 2( ) 2
27 6 ( ) 2 ( 3)
P x y z xy yz zx xyz
xy yz zx xyz
x y z yz x
025
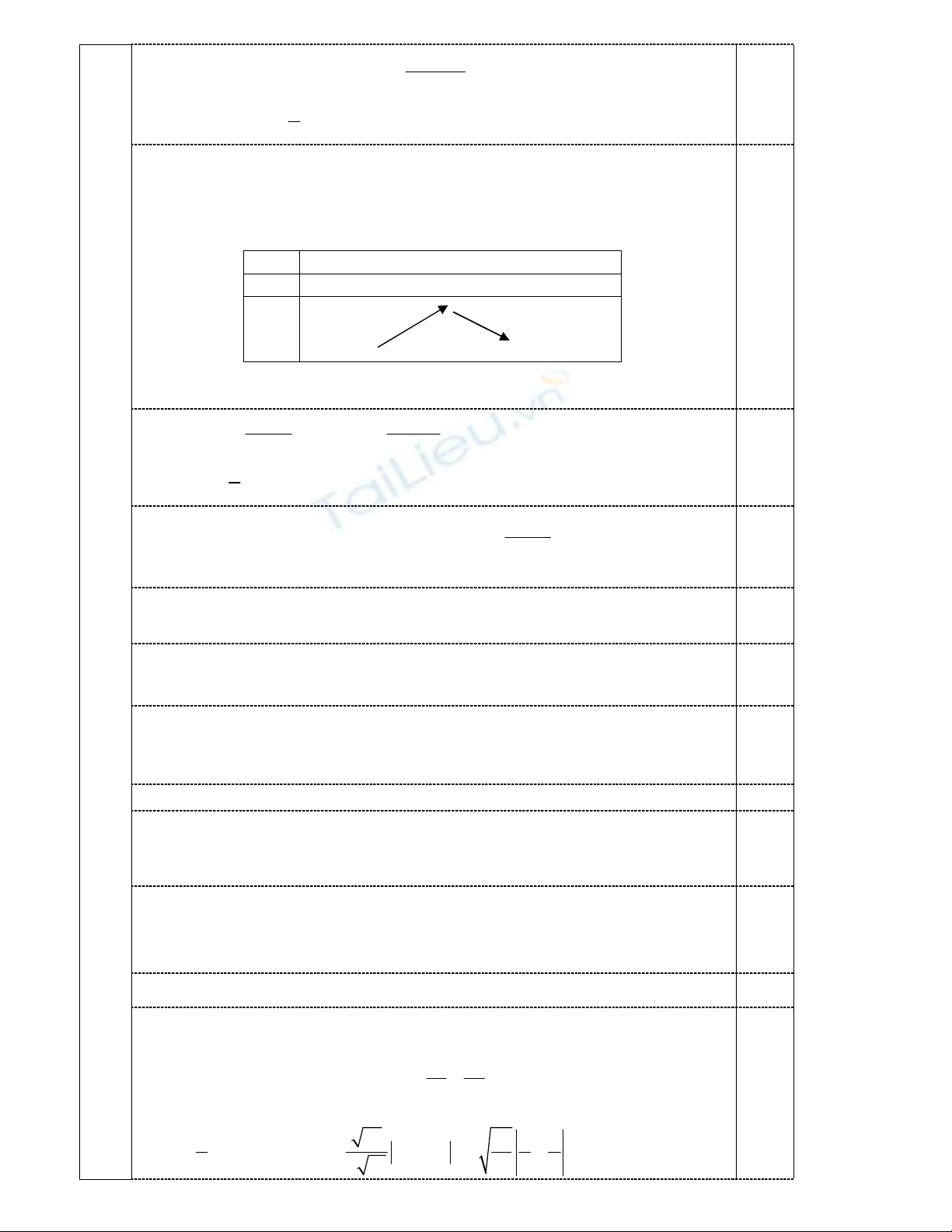
2
3 2
( )
27 6 (3 ) ( 3)
2
1( 15 27 27)
2
y z
x x x
x x x
025
Xét hàm số 3 2
( ) 15 27 27
f x x x x
, với 0<x<3
, 2
1
( ) 3 30 27 0
9
x
f x x x x
x

0 1 3

y’ + 0 -
y
14
Từ bảng biến thiên suy ra MinP=7
1
x y z
.
05
1. Gọi
3 4 16 3
( ; ) (4 ; )
4 4
a a
A a B a
. Khi đó diện tích tam giác ABC là
1
. ( ) 3
2
ABC
S AB d C AB
.
05
Theo giả thiết ta có
2
2
4
6 3
5 (4 2 ) 25
0
2
a
a
AB a a
Vậy hai điểm cần tìm là A(0;1) và B(4;4).
05
2. Ta có mặt cầu (S) có tâm I(1;-3;2) và bán kính R=4
Véc tơ pháp tuyến của
( )
là
(1;4;1)
n
025
Vì
( ) ( )
P
và song song với giá của
v
nên nhận véc tơ
(2; 1;2)
p
n n v
làm vtpt. Do đó (P):2x-y+2z+m=0
025
Vì (P) tiếp xúc với (S) nên
( ( )) 4
d I P
21
( ( )) 4
3
m
d I P m
025
Vậy có hai mặt phẳng : 2x-y+2z+3=0 và 2x-y+2z-21=0. 025
Ta có 10 10
2 10 2
10 10
0 0 0
(1 2 3 ) (2 3 ) ( 2 3 )
k
k k k i k i i k i
k
k k i
P x x C x x C C x
05
Theo giả thiết ta có
4
0 1 2
0 10
432
,
k i i i i
i k k k k
i k N
025
Vậy hệ số của
4
x
là: 4 4 3 1 2 2 2 2
10 10 3 10 2
2 2 3 3 8085
C C C C C . 025
VIa
VIIa
VIb
VIIb
1. Ta có PT đường thẳng AB:2x+3y=0
Gọi C(x;y) với x>0,y>0.Khi đó ta có 2 2
1
9 4
x y
và diện tích tam giác ABC
là
1 85 85
. ( ) 2 3 3
2 13 3 4
2 13
ABC
x y
S AB d C AB x y
05
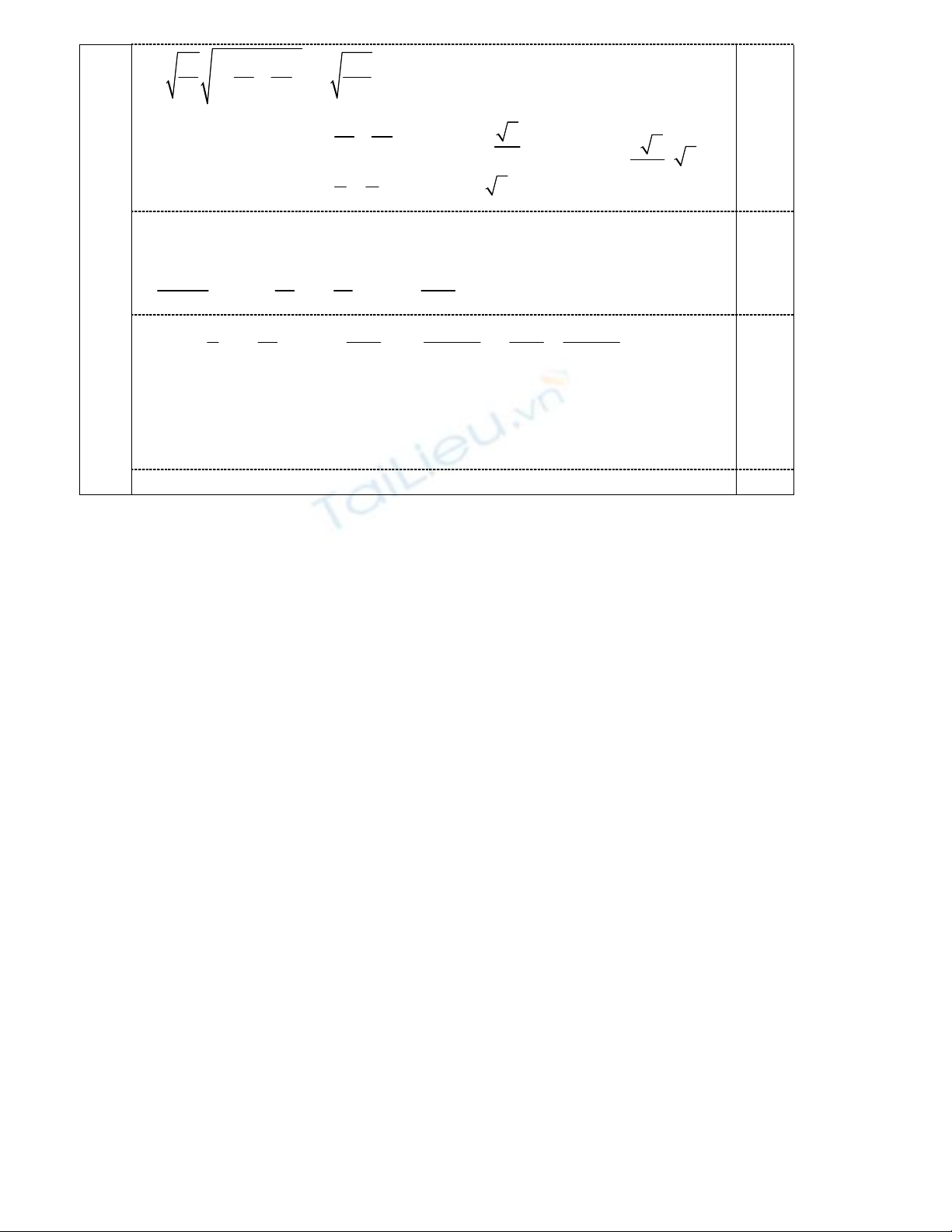
2 2
85 170
3 2 3
13 9 4 13
x y
Dấu bằng xảy ra khi
2 2
2
13
9 4
2
2
3 2
x y x
x y y
. Vậy 3 2
( ; 2)
2
C.
05
Xét khai triển 0 1 2 2
(1 ) ...
n n n
n n n n
x C C x C x C x
Lấy tích phân 2 vế cân từ 0 đến 2 , ta được:
1 2 3 1
0 1 3
3 1 2 2 2
2 ...
1 2 3 1
n n
n
n n n n
C C C C
n n
05
2 1 1
0 1 2
1
2 2 2 3 1 121 3 1
...
2 3 1 2( 1) 1 2( 1)
3 243 4
n n n
n
n n n n
n
C C C C
n n n n
n
Vậy n=4.
05