
http://ductam_tp.violet.vn/
SỞ GD & ĐT HƯNG YÊN ĐỀ THI THỬ ĐẠI HỌC NĂM 2011
TRƯỜNG THPT MINH CHÂU Môn toán - KHỐI A
Thời gian 180 phút ( không kể giao đề )
PHẦN A : DÀNH CHO TẤT CẢ CÁC THI SINH .
Câu I (2,0 điểm) 1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số : y = x3 – 3x2 + 2
2) Biện luận theo m số nghiệm của phương trình : 22 2
1
m
x x x
Câu II (2,0 điểm ) 1) Giải phương trình : 5
2 2 os sin 1
12
c x x
2) Giải hệ phương trình: 2 8
2 2 2 2
log 3log ( 2)
1 3
x y x y
x y x y
.
Câu III(1,0 điểm ) Tính tích phân:
/4
2
/4
sin
1
x
I dx
x x
Câu IV ( 1,0 điểm ) : Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a ,
AD = 2a . Cạnh SA vuông góc với mặt phẳng đáy , cạnh bên SB tạo với mặt phắng đáy một góc
600 .Trên cạnh SA lấy điểm M sao cho AM =
3
3
a, mặt phẳng ( BCM) cắt cạnh SD tại N .Tính
thể tích khối chóp S.BCNM
Câu V (1,0 điểm ) Cho x , y , z là ba số thực thỏa mãn : 5-x + 5-y +5-z = 1 .Chứng minh rằng
25 25 25
25 5 5 5 5 5
x y z
x y z y z x z x y
5 5 5
4
xyz
PHẦN B ( THÍ SINH CHỈ ĐƯỢC LÀM MỘT TRONG HAI PHẦN ( PHẦN 1 HOẶC PHẦN 2)
PHẦN 1 ( Dành cho học sinh học theo chương trình chuẩn )
Câu VI.a 1.( 1,0 điểm ) Trong mặt phẳng Oxy cho tam giác ABC với A(1; -2), đường cao
: 1 0
CH x y
, phân giác trong
:2 5 0
BN x y
.Tìm toạ độ các đỉnh B,C và tính diện tích
tam giác ABC
2.( 1,0 điểm ) Trong không gian với hệ tọa độ 0xyz cho đường thẳng d
2 1
4 6 8
x y z
và hai điểm A(1;-1;2) ,B(3 ;- 4;-2).Tìm điểm I trên đường thẳng d sao cho IA +IB đạt giá trị nhỏ
nhất
Câu VII.a (1 điểm): Giải phương trình sau trên tập số phức C: 2
4 3
1 0
2
z
z z z
PHẦN 2 ( Dành cho học sinh học chương trình nâng cao )
Câu VI.b 1. (1.0 điểm) Trong mặt phẳng với hệ trục toạ độ Oxy cho hình chữ nhật ABCD
có diện tích bằng 12, tâm I là giao điểm của đường thẳng 03:
1 yxd và
06:
2 yxd . Trung điểm của một cạnh là giao điểm của d1 với trục Ox. Tìm toạ độ
các đỉnh của hình chữ nhật.
2. (1,0điểm) Trong không gian với hệ tọa độ 0xyz cho hai đường thẳng :
D1 : 2 1
1 1 2
x y z
, D2 :
2 2
3
x t
y
z t
Viết phương trình mặt cầu có đường kính là đoạn vuông góc chung của D1 và D2
CâuVII.b ( 1,0 điểm) Tính tổng:
0 4 8 2004 2008
2009 2009 2009 2009 2009
...S C C C C C
…….Hết .......
ĐÁP ÁN
Cõu I 2 điểm
Khảo sát sự biến thiên và vẽ đồ thị của hàm số 3 2
3 2
y x x .
Tập xác định: Hàm số có tập xác định
D R.
Sự biến thiờn: 2
3 6
y' x x.
Ta có
0
0
2
x
y' x
0,25
0 2 2 2
CD CT
y y ; y y .
0,25
Bảng biến thiên:
x
0 2
y'
0
0
y
2
2
0,25
a)
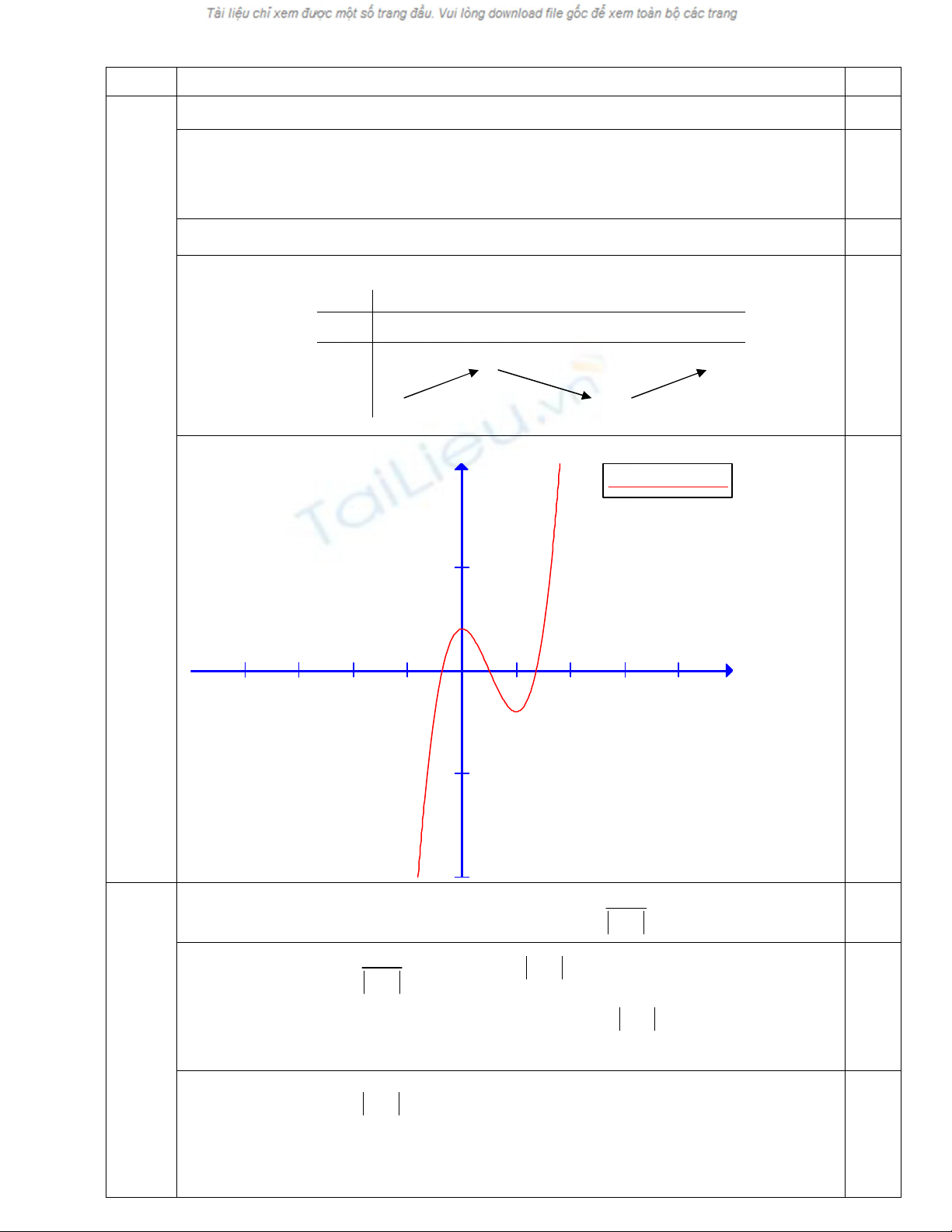
Đồ thị:
f(x)=(x^3)-3*(x)^2+2
-8 -6 -4 -2 2 4 6 8
-5
5
x
y
0,25
Biện luận số nghiệm của phương trình 1
22
2
x
m
xx theo tham số m.
Ta có
2 2
2 2 2 2 1 1
1
m
x x x x x m,x .
x
Do đó số nghiệm của
phương trình bằng số giao điểm của
22 2 1
y x x x , C'
và đường thẳng
1
y m,x .
0,25
b)
Vỡ
2
1
2 2 1
1
f x khi x
y x x x
f x khi x
nờn
C'
bao gồm:
+ Giữ nguyên đồ thị (C) bên phải đường thẳng
1
x .
+ Lấy đối xứng đồ thị (C) bên trái đường thẳng
1
x
qua Ox.
0,25
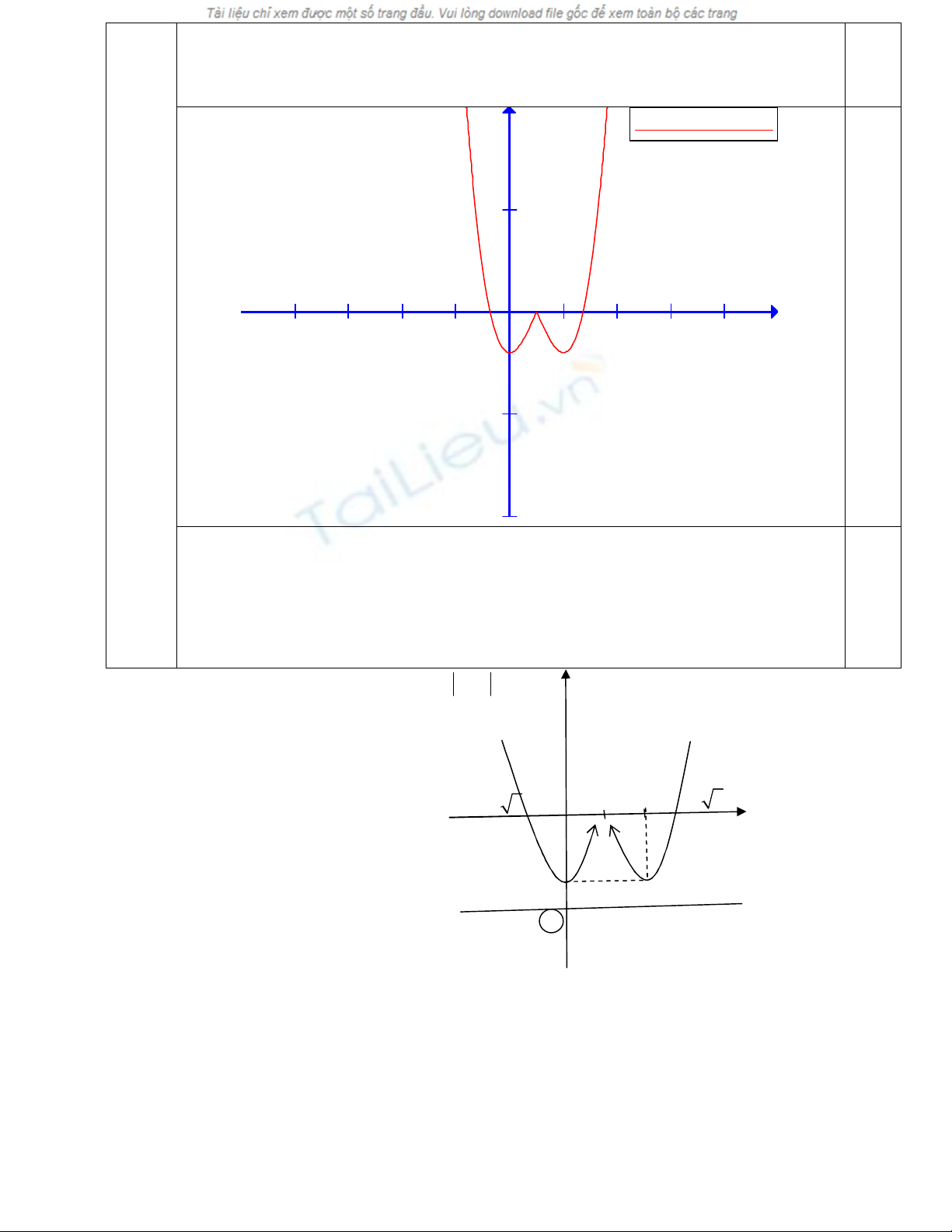
hình
f(x)=abs(x-1)(x^2-2*x-2)
-8 -6 -4 -2 2 4 6 8
-5
5
x
y
0,25
Dựa vào đồ thị ta có:
+
2
m :
Phương trình vụ nghiệm;
+
2
m :
Phương trình có 2 nghiệm kộp;
+
2 0
m :
Phương trình có 4 nghiệm phõn biệt;
+
0
m :
Phương trình có 2 nghiệm phõn biệt.
0,25
2) Đồ thị hàm số y = 2
( 2 2) 1
x x x
, với x
1 có dạng như hình vẽ :
1+
3
1-
3
- 2
m
1
2

II
1)
1) 5
2 2 os sin 1
12
c x x
5 5
2 sin 2 sin 1
12 12
x
0.25
5 5 1 5 5
sin 2 sin sin sin 2 sin sin
12 12 4 12 4 12
2
2cos sin sin
3 12 12
x x
0.25
5
2 2
5612 12
sin 2 sin 5 13 312 12 2 2
12 12 4
x kx k
x k
x k x k
0.5
2.) Giải hệ phương trình: 2 8
2 2 2 2
log 3log ( 2)
1 3
x y x y
x y x y
.
Điều kiện: x+y>0, x-y>0
2 8
2 2 2 2 2 2 2 2
log 3log (2 ) 2
1 3 1 3
x y x y x y x y
x y x y x y x y
0,25đ
Đặt:
u x y
v x y
ta có hệ: 2 2 2 2
2 ( ) 2 4
2 2
3 3
2 2
u v u v u v uv
u v u v
uv uv
0,25đ
2
2 4 (1)
( ) 2 2
3 (2)
2
u v uv
u v uv uv
. Thế (1) vào (2) ta có:
2
8 9 3 8 9 (3 ) 0
uv uv uv uv uv uv uv
.
0,25đ
Kết hợp (1) ta có: 0
4, 0
4
uv u v
u v
(vỡ u>v). Từ đó ta có: x =2; y =2.(T/m)
KL: Vậy nghiệm của hệ là: (x; y)=(2; 2).
0,25đ
Câu III 1 Tính tích phân :
/4
2
/4
sin
1
x
I dx
x x
/4 /4 /4
2
1 2
2
/4 /4 /4
sin 1 sin sin
1
x
I dx x xdx x xdx I I
x x
Áp dụng hàm lẻ, đặt x=-t thì 1
0
I
, tích phân từng phần
2
I
được kết quả.
0.5đ
Áp dụng hàm lẻ, đặt x=-t thì 1
0
I
, tích phân từng phần
2
I
được kết quả. 0.5đ
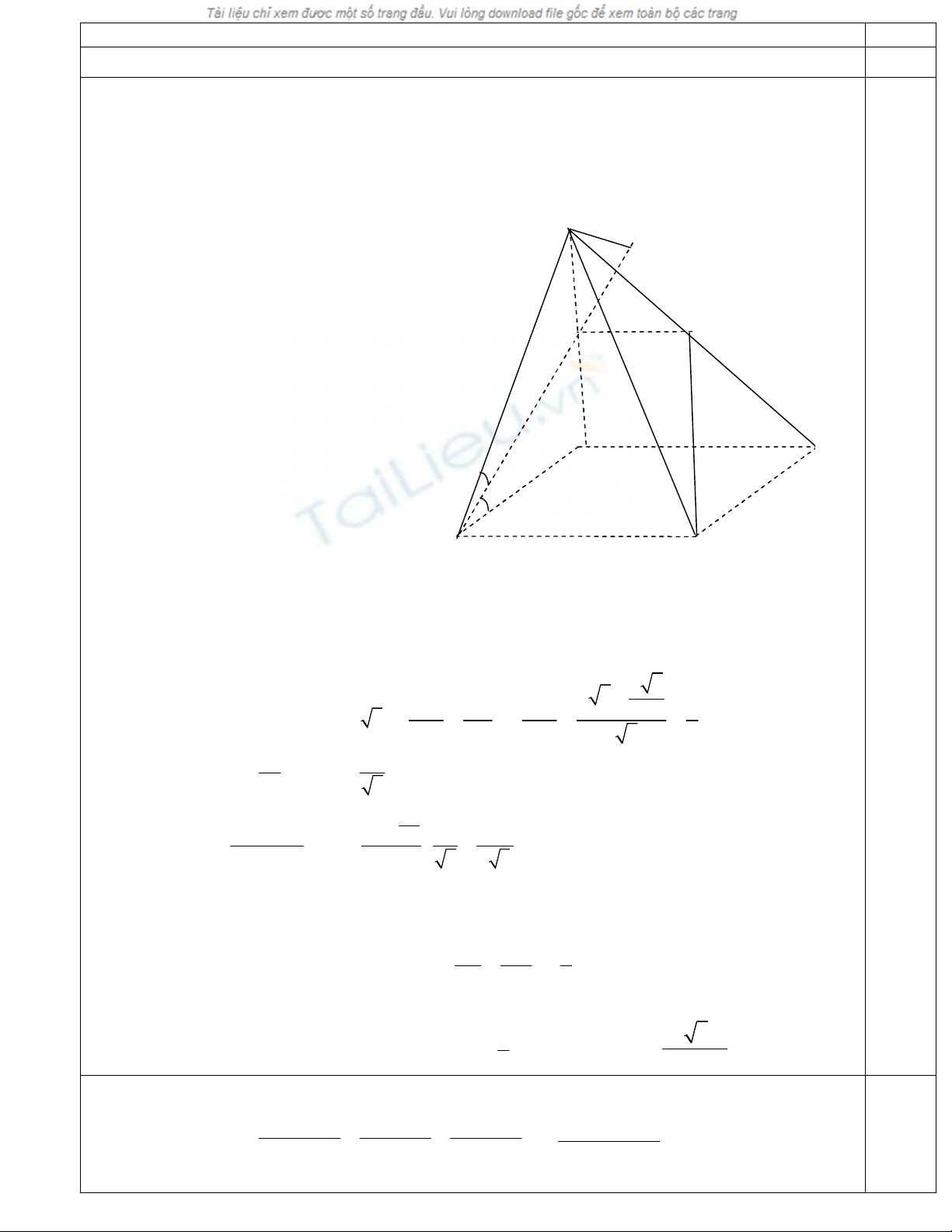
Câu IV :
Tính thể tích hình chóp SBCMN
( BCM)// AD nên mặt phẳng này cắt mp( SAD) theo giao tuyến MN // AD
Ta có : BC AB
BC BM
BC SA
. Tứ giác BCMN là hình thang vuông có BM là đường
cao
Ta có SA = AB tan600 = a
3
,
3
3
2
3
2 3
3
a
a
MN SM MN
AD SA a a
Suy ra MN =
4
3
a
. BM =
2
3
a
Diện tích hình thang BCMN là :
S =
2
4
2
2 10
3
2 2
3 3 3
a
a
BC MN a a
BM
Hạ AH
BM . Ta có SH
BM và BC
(SAB)
BC
SH . Vậy SH
( BCNM)
SH là đường cao của khối chóp SBCNM
Trong tam giác SBA ta có SB = 2a ,
AB AM
SB MS
=
1
2
.
Vậy BM là phân giác của góc SBA
0
30
SBH
SH = SB.sin300 = a
Gọi V là thể tích chóp SBCNM ta có V = 1
.( )
3
SH dtBCNM
=
3
10 3
27
a
0,25đ
0,25đ
0,25đ
0,25đ
Câu V Cho x , y , z là ba số thực thỏa mãn : 5-x + 5-y +5-z = 1 .Chứng minh rằng :
25 25 25
25 5 5 5 5 5
x y z
x y z y z x z x y
5 5 5
4
xyz
Đặt 5x = a , 5y =b , 5z = c . Từ giả thiết ta có : ab + bc + ca = abc
A
S
B
C
M
N
D












![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)




![Đề thi học kì 2 Vật lý lớp 11: Đề minh họa [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250709/linhnhil/135x160/711752026408.jpg)








