Đ THI TH ĐI H CỀ Ử Ạ Ọ NĂM 2014.
Môn thi: TOÁN
Th i gian làm bài:ờ 180 phút
Đ S 5-BBỀ Ố
A. PH N CHUNG CHO T T C THÍ SINH (7Ầ Ấ Ả đi mể)
Câu I. (2 đi m) ể
Cho hàm s ốy = x3 + 3x2 + mx + 1 có đ th là (ồ ị Cm); ( m là tham s )ố
1. Kh o sát s bi n thiên và v đ th hàm s khi ả ự ế ẽ ồ ị ố m = 3.
2. Xác đnh m đ (ị ể Cm) c t đng th ng ắ ườ ẳ y = 1 t i ba đi m phân bi t ạ ể ệ C(0;1), D, E sao cho các ti p tuy nế ế
c a ủ
(Cm) t i ạD và E vuông góc v i nhau.ớ
Câu II (2 đi m) ể
1.Gi i ph ng trình: ả ươ
x
xx
xx 2
32
2
cos
1coscos
tan2cos
.
2. Gi i h ph ng trìnhả ệ ươ :
2 2
2 2
1 4
( ) 2 7 2
x y xy y
y x y x y
+ + + =
+ = + +
( , )x yR
.
Câu III (1 đi m) Tính tích phân: ể
3
2
2
1
log
1 3ln
e
x
I dx
x x
=+
.
Câu IV. (1 đi m) ể
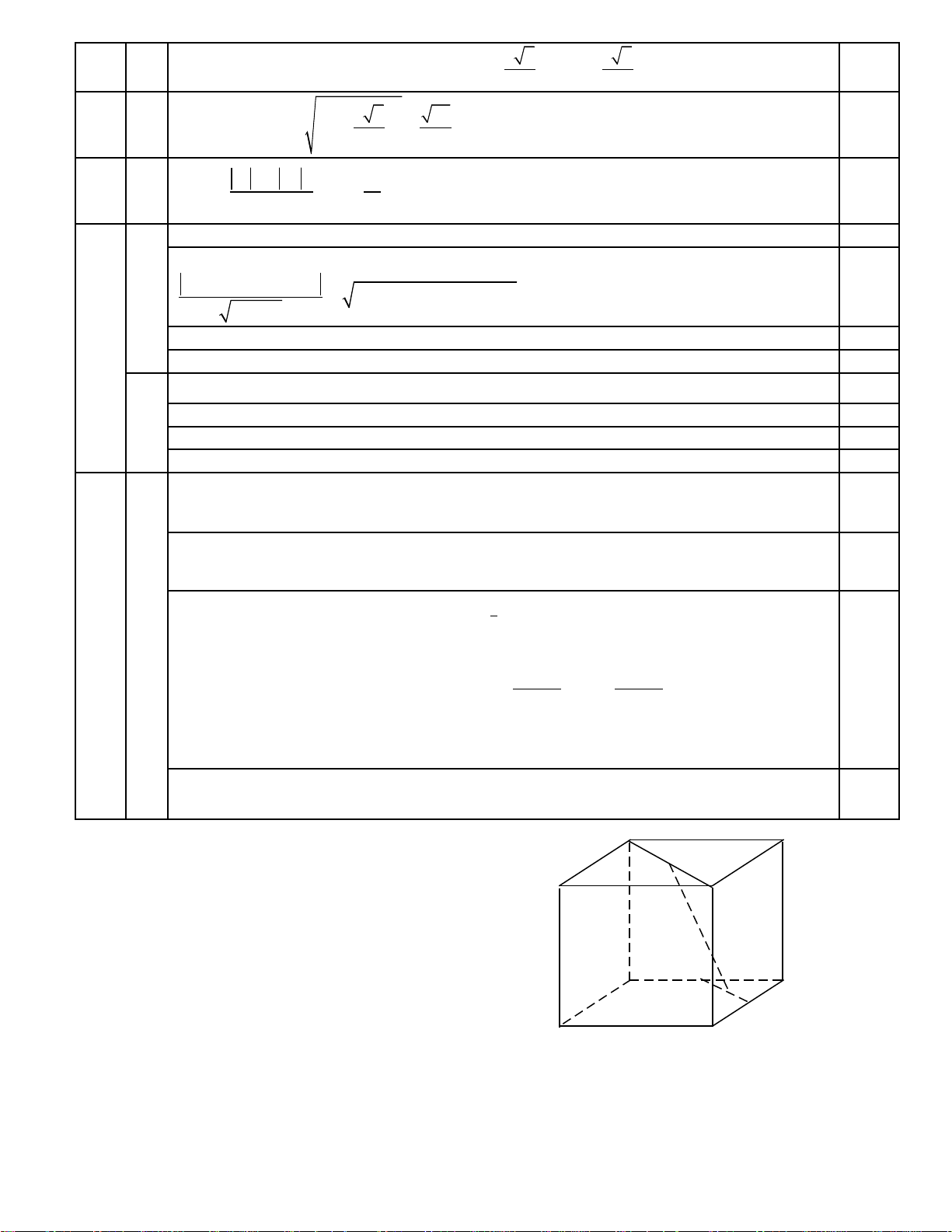
Cho h×nh hép ®øng ABCD.A'B'C'D' cã c¸c c¹nh AB = AD = a, AA' =
3
2
a
vµ gãc BAD = 600. Gäi
M vµ N
lÇn lît lµ trung ®iÓm cña c¸c c¹nh A'D' vµ A'B'. Chøng minh AC' vu«ng gãc víi mÆt ph¼ng
(BDMN). TÝnh
thÓ tÝch khèi chãp A.BDMN.
Câu V. (1 đi m)ể
Cho a, b, c là các s th c không âm th a mãn ố ự ỏ
1abc+ + =
. Ch ng minh r ngứ ằ :
7
227
ab bc ca abc+ + −
.
B. PH N RIÊNGẦ (3 đi mể). Thí sinh ch đc làm m t trong hai ph n (ph n ỉ ượ ộ ầ ầ 1 ho c ặ2)
1.Theo ch ng trình Chu nươ ẩ
Câu VIa. ( 2 đi m)ể
1. Trong m t ph ng v i h t a đ ặ ẳ ớ ệ ọ ộ Oxy , cho tam giác ABC bi t ếA(5; 2). Ph ng trình đng trung tr cươ ườ ự
c nh ạBC, đng trung tuy n ườ ế CC’ l n l t là ầ ượ x + y – 6 = 0 và 2x – y + 3 = 0. Tìm t a đ các đnh c a ọ ộ ỉ ủ
tam giác ABC.
2. Trong không gian v i h t a đ ớ ệ ọ ộ Oxyz, hãy xác đnh to đ tâm và bán kính đng tròn ngo i ti p ị ạ ộ ườ ạ ế
tam
giác ABC, bi t ếA(-1; 0; 1), B(1; 2; -1), C(-1; 2; 3).
Câu VIIa. (1 đi m)ể
Cho
1
z
,
là các nghi m ph c c a ph ng trình ệ ứ ủ ươ
2
2 4 11 0z z− + =
. Tính giá tr c a bi u th cị ủ ể ứ
2 2
1 22
1 2
( )
z z
z z
+
+
.
2. Theo ch ng trình Nâng cao ươ
Câu VIb. ( 2 đi m)ể
1. Trong m t ph ng v i h t a đ ặ ẳ ớ ệ ọ ộ Oxy cho hai đng th ngườ ẳ
∆
:
3 8 0x y+ + =
,
':3 4 10 0x y∆ − + =
và
đi m ể
A(-2 ; 1). Vi t ph ng trình đng tròn có tâm thu c đng th ng ế ươ ườ ộ ườ ẳ
∆
, đi qua đi m ểA và ti p xúc v i ế ớ
đng ườ
th ng ẳ
∆
’.
2. Trong không gian v i h t a đ ớ ệ ọ ộ Oxyz, Cho ba đi m ểA(0;1;2), B(2;-2;1), C(-2;0;1). Vi t ph ng trình ế ươ
m t ph ng (ặ ẳ ABC) và tìm đi m ểM thu c m t ph ng 2ộ ặ ẳ x + 2y + z – 3 = 0 sao cho MA = MB = MC.
Câu VIIb. (1 đi m)ể
Gi i h ph ng trìnhả ệ ươ :
2
1 2
1 2
2log ( 2 2) log ( 2 1) 6
log ( 5) log ( 4) = 1
x y
x y
xy x y x x
y x
− +
− +
− − + + + − + =
+ − +
,
( , )x yR
.
----------Hết ----------
H và tên thí sinh: ………………………………………………; S báo danh: …ọ ố BB01064……..
CâuÝN i dungộĐiể
m
I 1 1
2 PT hoành đ giao đi m ộ ể x3 + 3x2 + mx + 1 = 1
x(x2 + 3x + m) = 0
m = 0, f(x) =
00.25
Đê th a mãn yc ta ph i có pt f(x) = 0 có 2 nghi m phân bi t xỏ ả ệ ệ 1, x2 khác 0 và
y’(x1).y’(x2) = -1. 0.25
Hay
2 2
1 1 2 2
9 4 0, (0) 0
(3 6 )(3 6 ) 1.
m f m
x x m x x m
− > =
+ + + + = −
2 2 2 2 2
1 2 1 2 1 2 1 2 1 2 1 2
99
, 0 , 0
44
9( ) 18 ( ) 3 ( ) 36 6 ( ) 1 4 9 1 0
m m m m
x x x x x x m x x x x m x x m m m
< <
� �
� �
� �
� �
+ + + + + + + + = − − + =
0.25
Gi i ra ta có ĐS: m = ả
9 65
8
0.25
II 1 ĐK cosx ≠ 0, pt đc đa vượ ư ề
2 2 2
cos2 tan 1 cos (1 tan ) 2cos cos -1 0x x x x x x− = + − + − =�
0.5
Gi i ti p đc cosx = 1 và cosx = 0,5 r i đi chi u đk đ đa ra ĐS:ả ế ượ ồ ố ế ể ư
2 2
2 , 2 ; hay
3 3
x k x k x k
π π
π π
= = + =
.0.5
2
0y
, ta có:
2
2 2
2 2 2
2
14
1 4 .
( ) 2 7 2 1
( ) 2 7
xx y
y
x y xy y
y x y x y x
x y y
++ + =
+ + + =
� �
+ = + + +
+ − =
0.25
Đt ặ
2
1,
x
u v x y
y
+
= = +
ta có h : ệ
2 2
4 4 3, 1
2 7 2 15 0 5, 9
u v u v v u
v u v v v u
+ = = − = =
� � �
� �
� �
− = + − = = − =
� � �
0.25
+) V i ớ
3, 1v u= =
ta có h :ệ
2 2 2
1, 2
1 1 2 0
2, 5
3 3 3
x y
x y x y x x
x y
x y y x y x
= =
���
+ = + = + − =
� � �
��� = − =
+ = = − = −
���
.0.25
+) V i ớ
5, 9v u= − =
ta có h : ệ
2 2 2
1 9 1 9 9 46 0
5 5 5
x y x y x x
x y y x y x
���
+ = + = + + =
� �
���
+ = − = − − = − −
���
, h nàyệ
vô nghi m.ệ
KL: V y h đã cho có hai nghi m: ậ ệ ệ
( ; ) {(1; 2), ( 2; 5)}.x y = −
0.25
III
3
32
2
3
2 2 2
1 1 1
ln
log 1 ln . ln
ln 2 .
ln 2
1 3ln 1 3ln 1 3ln
e e e
x
x x xdx
I dx dx x
x x x x x
� �
� �
� �
===
+ + +
� � �
0.25
Đt ặ
2 2 2
1 1
1 3ln ln ( 1) ln .
3 3
dx
x t x t x tdt
x
+ = = − =� �
. Đi c n …ổ ậ 0.25
Suy ra
( ) ( )
2
2 2
32
2
3 3
2
1 1 1
11
log 1 1 1
3. 1
ln 2 3 9ln 2
1 3ln
e
t
x
I dx tdt t dt
t
x x
−
= = = −
+
� � �
0.25
2
3
3 3
1
1 1 4
9ln 2 3 27ln 2
t t
� �
= − =
� �
� �
0.25
IV Ch ng t AC’ứ ỏ
⊥
BD 0.25
C/m AC’
⊥
PQ, v i P,Q là trung đi m c a BD, MN. Suy ra AC’ớ ể ủ
⊥
(BDMN) 0.25
Tính đúng chi u cao AH , v i H là giao c a PQ và AC’. N u dùng cách hi u các th ề ớ ủ ế ệ ể
tích thì ph i ch ra cách tính.ả ỉ 0.25
Tính đúng di n tích hình thang BDMN . Suy ra th tích c n tìm là: ệ ể ầ
3
3
16
a
.0.25
VTa có
2 ( ) (1 2 ) (1 ) (1 2 )ab bc ca abc a b c a bc a a a bc+ + − = + + − = − + −
. Đt t= bc thì ta ặ
có
2 2
( ) (1 )
04 4
b c a
t bc + −
= =
.Xét hs f(t) = a(1- a) + (1 – 2a)t trên đo n ạ
2
(1 )
0; 4
a
� �
−
� �
� �
0.5
Có f(0) = a(1 – a)
2
( 1 ) 1 7
4 4 27
a a+ −
= <
và
2
2
(1 ) 7 1 1 1 7
(2 )
4 27 4 3 3 27
a
f a a
� �
−� �
= − + −
� � � �
� � � �
� �
v i m i a ớ ọ
[ ]
0;1
0,25
V y ậ
7
227
ab bc ca abc+ + −
. Đng th c x y ra khi a = b = c = 1/3ẳ ứ ả 0.25
VIa. 1. Gäi C = (c; 2c+3) vµ I = (m; 6-m) lµ trung ®iÓm cña BC
Suy ra: B= (2m-c; 9-2m-2c). V× C’ lµ trung ®iÓm cña AB nªn:
2 5 11 2 2
' ; '
2 2
m c m c
C CC
− + − −
� �
=
� �
� �
nªn
2 5 11 2 2 5
2( ) 3 0
2 2 6
m c m c m
− + − −
− + = = −�
5 41
( ; )
6 6
I= −�
. Ph¬ng tr×nh BC: 3x – 3y + 23=0
Täa ®é cña C lµ nghiÖm cña hÖ:
2 3 0 14 37
;
3 3 23 0 3 3
x y C
x y
− + =
� �
=�
� �
− + = � �
0.5
Täa ®é cña B =
19 4
;
3 3
� �
−
� �
� �
0.5
2. Ta có:
(2; 2; 2), (0; 2;2).AB AC= − =
uuur uuur
Suy ra ph ng trình m t ph ng trung tr c c a ươ ặ ẳ ự ủ
AB, AC là:
1 0, 3 0.x y z y z+ − − = + − =
0.25
Vect pháp tuy n c a mp(ơ ế ủ ABC) là
, (8; 4;4).n AB AC
� �
= = −
� �
r uuur uuur
Suy ra (ABC):
2 1 0x y z− + + =
.0.25
Gi i h : ả ệ
1 0 0
3 0 2
2 1 0 1
x y z x
y z y
x y z z
+ − − = =
� �
� �
+ − = =�
� �
� �
− + + = =
� �
. Suy ra tâm đng tròn là ườ
(0; 2;1).I
0.25
Bán kính là
2 2 2
( 1 0) (0 2) (1 1) 5.R IA= = − − + − + − =
0.25
VII
aGi i pt đã cho ta đc các nghi m: ả ượ ệ
1 2
3 2 3 2
1 , 1
2 2
z i z i= − = +
0.5
Suy ra
2
2
1 2 1 2
3 2 22
| | | | 1 ; 2
2 2
z z z z
� �
= = + = + =
� �
� �
� �
0.25
Đo đó
2 2
1 22
1 2
11
... 4
( )
z z
z z
+= =
+
0.25
VIb 1. Tâm I c a đng tròn thu c ủ ườ ộ
∆
nên I(-3t – 8; t) 0.25
Theo yc thì k/c t I đn ừ ế
∆
’ b ng k/c IA nên ta cóằ
2 2
2 2
3( 3 8) 4 10 ( 3 8 2) ( 1)
3 4
t t t t
− − − + = − − + + −
+
0.25
Gi i ti p đc t = -3 ả ế ượ 0.25
Khi đó I(1; -3), R = 5 và pt c n tìm: (x – 1)ầ2 + (y + 3)2 = 25. 0.25
2. Ta có
(2; 3; 1), ( 2; 1; 1) (2;4; 8)AB AC n= − − = − − − = −�
uuur uuur r
là 1 vtpt c a (ABC)ủ0.25
Suy ra pt (ABC) là (x – 0) + 2(y – 1) – 4(z – 2) = 0 hay x + 2y – 4z + 6 = 0 0.25
M(x; y; z) MA = MB = MC
…. 0.25
M thu c mp: 2x + 2y + z – 3 = 0 nên ta có h , gi i h đc x = 2, y = 3, z = -7ộ ệ ả ệ ượ 0.25
VII
b+ Đi u ki n: ề ệ
2
2 2 0, 2 1 0, 5 0, 4 0 ( )
0 1 1, 0 2 1
xy x y x x y x I
x y
− − + + > − + > + > + >
< − < +
. 0.25
1 2 1 2
1 2 1 2
2log [(1 )( 2)] 2log (1 ) 6 log ( 2) log (1 ) 2 0 (1)
( ) log ( 5) log ( 4) = 1 log ( 5) log ( 4) = 1(2).
x y x y
x y x y
x y x y x
Iy x y x
− + − +
− + − +
− + + − = + + − − =
� �
� �
� �
� �
+ − + + − +
� �
� �
0.25
Đt ặ
2
log (1 )
y
x t
+
− =
thì (1) tr thành: ở
2
12 0 ( 1) 0 1.t t t
t
+ − = − = =� �
V i ớ
1t=
ta có:
1 2 1(3).x y y x− = + = − −�
Th vào (2) ta có:ế
2
1 1 1
4 4
log ( 4) log ( 4) = 1 log 1 1 2 0
4 4
x x x
x x
x x x x x
x x
− − −
− + − +
− + − + = = − + =� � �
+ +
0
2
x
x
=
= −
. Suy ra:
1
1
y
y
= −
=
.
0.25
+ Ki m tra th y ch có ể ấ ỉ
2, 1x y= − =
tho mãn đi u ki n trên.ả ề ệ
V y h có nghi m duy nh t ậ ệ ệ ấ
2, 1x y= − =
.0.25
A
B
D
P
M
N
Q