Đ THI TH ĐI H CỀ Ử Ạ Ọ NĂM 2014.
Môn thi: TOÁN
Th i gian làm bài:ờ 180 phút
Đ S 6-BBỀ Ố
PHẦN CHUNG CHO T T C THÍ SINH (7,0 đi m)Ấ Ả ể
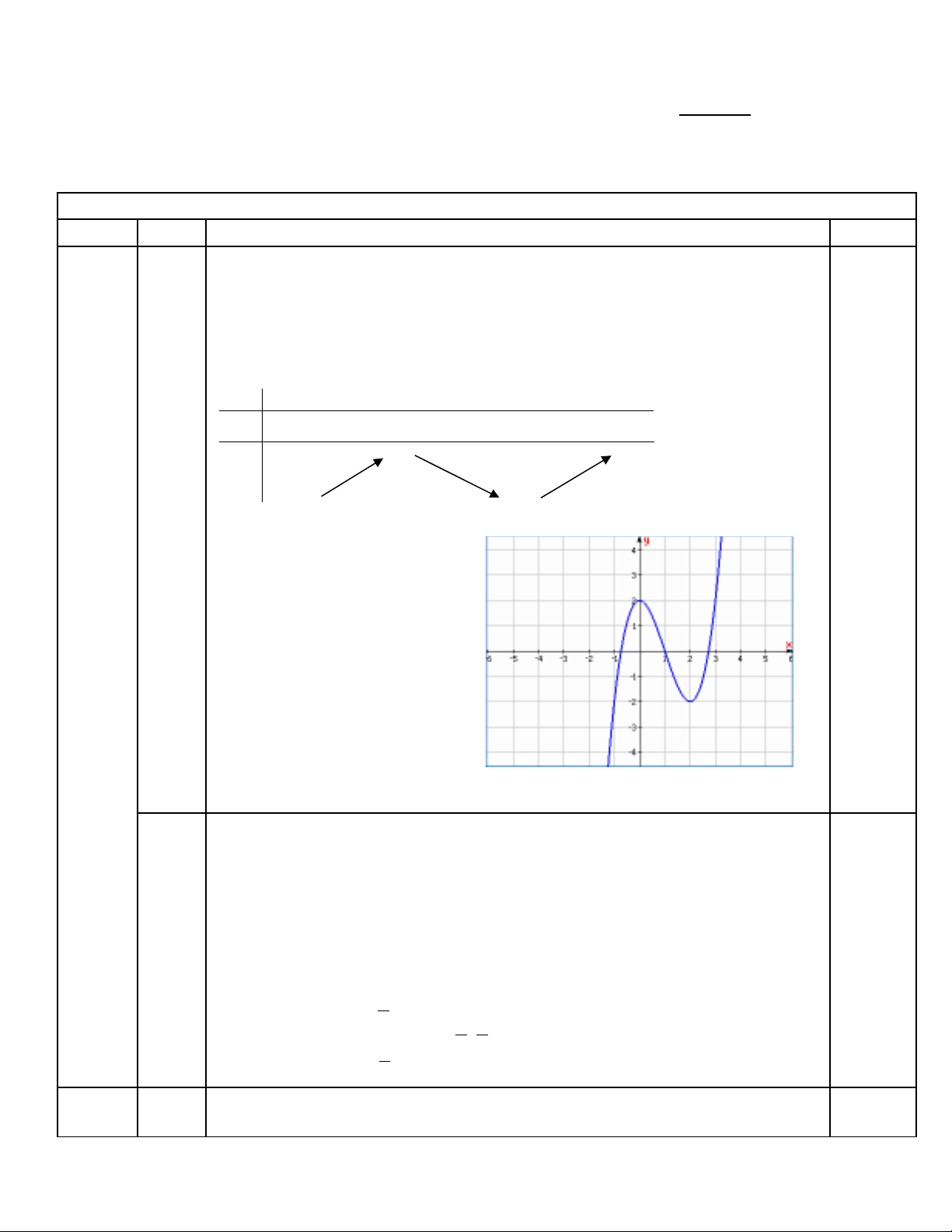
Câu I (2 đi m) Cho hàm s y = xể ố 3 – 3x2+2 (1)
1. Kh o sát s bi n thiên và v đ th c a hàm s (1).ả ự ế ẽ ồ ị ủ ố
2. Tìm đi m M thu c đng th ng y=3x-2 sao t ng kho ng cách t M t i hai đi m c c tr nhể ộ ườ ẳ ổ ả ừ ớ ể ự ị ỏ
nh t.ấ
Câu II (2 đi m)ể
1. Gi i ph ng trình ả ươ
cos2x 2sin x 1 2sin x cos 2x 0+ − − =
2. Gi i b t ph ng trình ả ấ ươ
( )
2
4x 3 x 3x 4 8x 6− − + −
Câu III ( 1đi m)Tính tích phân ể
3
6
cotx
I dx
sinx.sin x 4
π
π
=π
� �
+
� �
� �
Câu IV (1 đi m)ể
Cho hình chóp S.ABC có m t đáy (ABC) là tam giác đu c nh a. Chân đng vuông góc h tặ ề ạ ườ ạ ừ
S xu ng m t ph ng (ABC) là m t đi m thu c BC. Tính kho ng cách gi a hai đng th ng BCố ặ ẳ ộ ể ộ ả ữ ườ ẳ
và SA bi t SA=a và SA t o v i m t ph ng đáy m t góc b ng 30ế ạ ớ ặ ẳ ộ ằ 0.
Câu V (1 đi m) Cho a,b, c d ng và aể ươ 2+b2+c2=3. Tìm giá tr nh nh t c a bi u th cị ỏ ấ ủ ể ứ
3 3 3
2 2 2
3 3 3
a b c
P
b c a
= + +
+ + +
PH N RIÊNG (3 đi m)Ầ ể
A. Theo ch ng trình chu nươ ẩ
Câu VI.a. (2 đi m)ể
1. Trong m t ph ng v i h to đ Oxy, cho đng tròn (C) : ặ ẳ ớ ệ ạ ộ ườ
2 2
x y 2x 8y 8 0+ + − − =
. Vi tế
ph ng trình đng th ng song song v i đng th ng d: 3x+y-2=0 và c t đng tròn theoươ ườ ẳ ớ ườ ẳ ắ ườ
m t dây cung có đ dài b ng 6.ộ ộ ằ
2. Cho ba đi m A(1;5;4), B(0;1;1), C(1;2;1). Tìm t a đ đi m D thu c đng th ng AB saoể ọ ộ ể ộ ườ ẳ
cho đ dài đo n th ng CD nh nh t. ộ ạ ẳ ỏ ấ
Câu VII.a (1 đi m)ể
Tìm s ph c z tho mãn : ố ứ ả
z 2 i 2−+=
. Bi t ph n o nh h n ph n th c 3 đn v .ế ầ ả ỏ ơ ầ ự ơ ị
B. Theo ch ng trình nâng caoươ
Câu VI.b (2 đi m)ể
1. Tính giá tr bi u th c: ị ể ứ
2 4 6 100
100 100 100 100
4 8 12 ... 200A C C C C= + + + +
.
2. Cho hai đng th ng có ph ng trình:ườ ẳ ươ
1
2 3
: 1
3 2
x z
d y
− +
= + =
Vi t ph ng trình đng th ng c t dế ươ ườ ẳ ắ 1 và d2 đng th i đi qua đi m M(3;10;1).ồ ờ ể
1
Câu VII.b (1 đi m)Gi i ph ng trình sau trên t p ph c: zể ả ươ ậ ứ 2+3(1+i)z-6-13i=0
----------H t ----------ế
H và tên thí sinh: ………………………………………………; S báo danh: …ọ ố BB01064……..
PH N CHUNG CHO T T C THÍ SINH (7,0 đi m)Ầ Ấ Ả ể
Câu N i dungộĐi mể
I
1
T p xác đnh: D=Rậ ị
( ) ( )
3 2 3 2
lim 3 2 lim 3 2
x x
x x x x
− +
− + = − − + = +
y’=3x2-6x=0
0
2
x
x
=
=
B ng bi n thiên:ả ế
x - 0 2 +
y’ + 0 - 0 +
2 +
y
- -2
Hàm s đng bi n trênố ồ ế
kho ng: (-ả;0) và (2; + )
Hàm s ngh ch bi n trênố ị ế
kho ng (0;2)ả
fCĐ=f(0)=2; fCT=f(2)=-2
y’’=6x-6=0<=>x=1
khi x=1=>y=0
x=3=>y=2
x=-1=>y=-2
Đ th hàm s nh n đi m I(1;0) là tâm đi x ng.ồ ị ố ậ ể ố ứ
0,25 đ
0,25 đ
0,5 đ
2
G i t a đ đi m c c đi là A(0;2), đi m c c ti u B(2;-2)ọ ọ ộ ể ự ạ ể ự ể
Xét bi u th c P=3x-y-2ể ứ
Thay t a đ đi m A(0;2)=>P=-4<0, thay t a đ đi m B(2;-2)=>P=6>0ọ ộ ể ọ ộ ể
V y 2 đi m c c đi và c c ti u n m v hai phía c a đng th ngậ ể ự ạ ự ể ằ ề ủ ườ ẳ
y=3x-2, đ MA+MB nh nh t => 3 đi m A, M, B th ng hàngể ỏ ấ ể ẳ
Ph ng trình đng th ng AB: y=-2x+2ươ ườ ẳ
T a đ đi m M là nghi m c a h :ọ ộ ể ệ ủ ệ
4
3 2 5
2 2 2
5
x
y x
y x y
=
= −
� �
= − +
=
=>
4 2
;
5 5
M� �
� �
� �
0,25 đ
0,25 đ
0,25 đ
0,25 đ
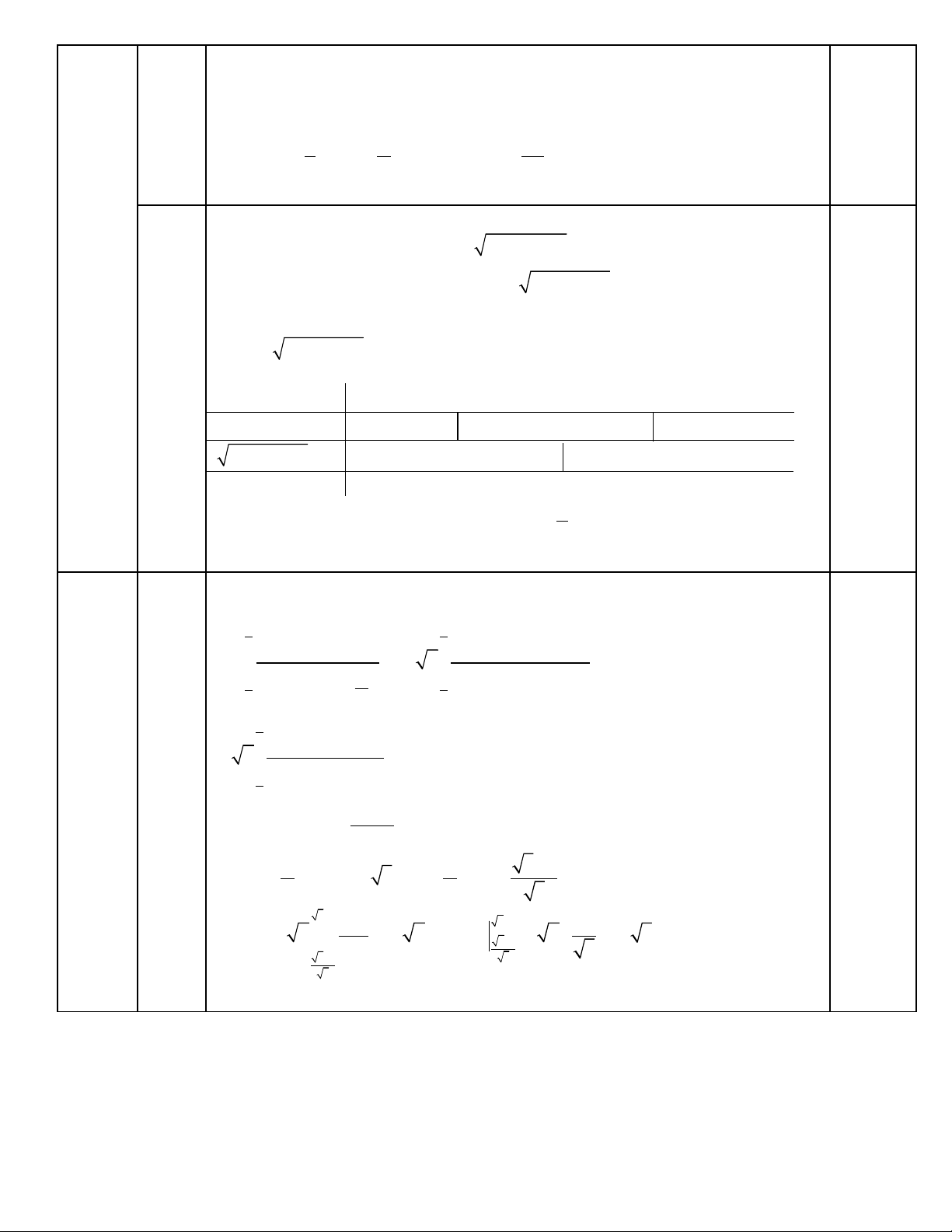
II 1 Gi i ph ng trình: ả ươ
cos2x 2sin x 1 2sin x cos 2x 0
+ − − =
(1)
2
( ) ( ) ( )
( ) ( )
1 os2 1 2sin 1 2sin 0
os2 1 1 2sin 0
c x x x
c x x
− − − =�
− − =�
Khi cos2x=1<=>
x k
π
=
,
k Z
Khi
1
sinx 2
=
2
6
x k
ππ
= +
ho c ặ
52
6
x k
ππ
= +
,
k Z
0,5 đ
0,5 đ
2
Gi i b t ph ng trình: ả ấ ươ
( )
2
4x 3 x 3x 4 8x 6− − + −
(1)
(1)
( )
()
2
4 3 3 4 2 0x x x− − + −� �
Ta có: 4x-3=0<=>x=3/4
2
3 4 2x x− + −
=0<=>x=0;x=3
B ng xét d u: ả ấ
x - 0 ¾ 2 +
4x-3 - - 0 + +
2
3 4 2x x− + −
+ 0 - - 0 +
V trái - 0 + 0 - 0 +ế
V y b t ph ng trình có nghi m: ậ ấ ươ ệ
[
)
3
0; 3;
4
x� � +� � �
� �
� �
0,25 đ
0,25 đ
0,25 đ
0,25 đ
III
Tính
( )
( )
3 3
6 6
3
2
6
cot cot
2sinx sinx cos
sin x sin 4
cot
2sin x 1 cot
x x
I dx dx
x
x
xdx
x
π π
π π
π
π
π
= = +
� �
+
� �
� �
=+
� �
Đt 1+cotx=tặ
2
1
sin dx dt
x= −�
Khi
3 1
1 3;
6 3 3
x t x t
π π
+
= = + = =� �
V y ậ
( )
3 1 3 1
3 1
3
3 1
3
1 2
2 2 ln 2 ln 3
3
t
I dt t t
t
++
+
+
−� �
= = − = −
� �
� �
0,25 đ
0,25 đ
0,25 đ
0,25 đ
3
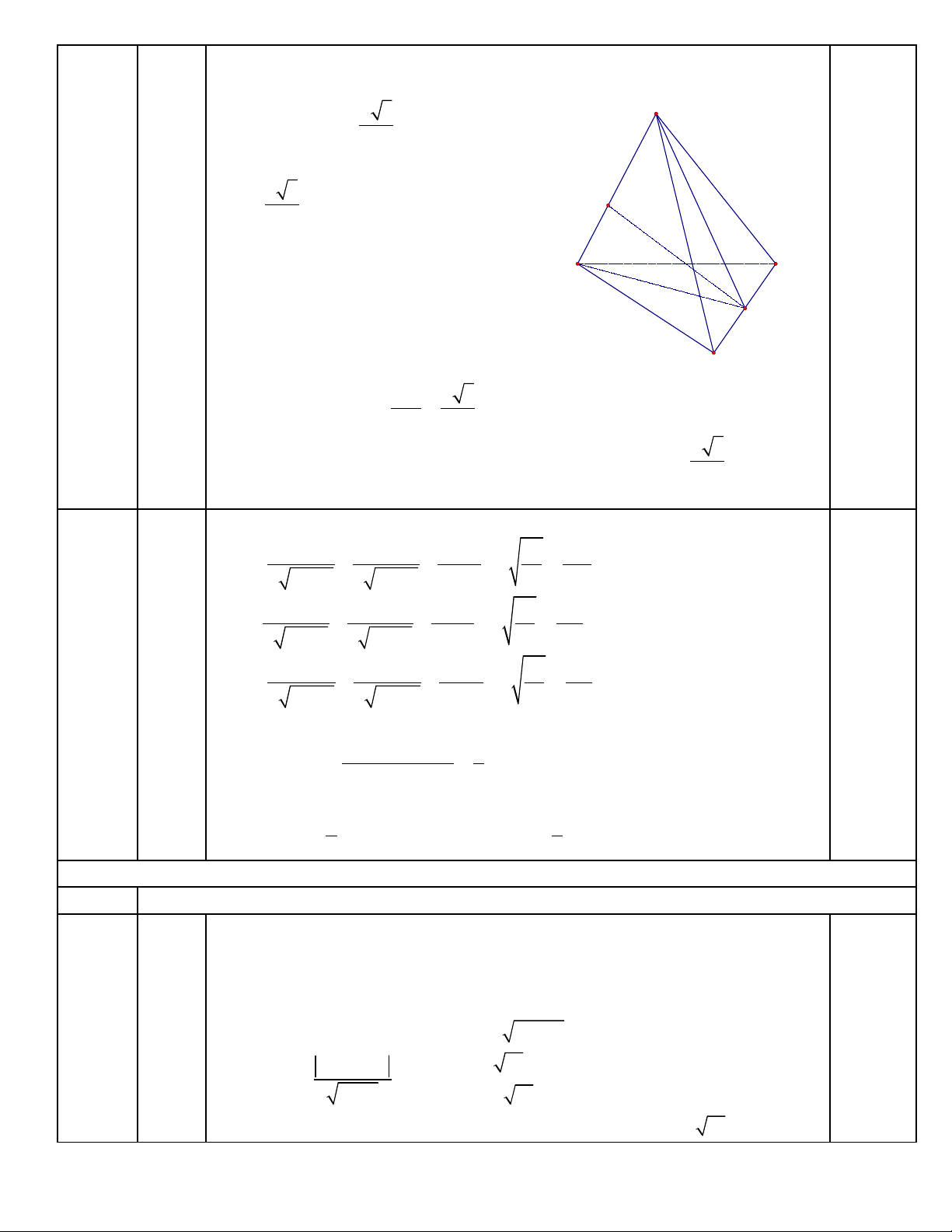
IV
G i chân đng vuông góc h t S xu ng BC là H.ọ ườ ạ ừ ố
Xét SHA(vuông t i H)ạ
0
3
cos30 2
a
AH SA= =
Mà ABC đu c nh a, mà c nhề ạ ạ
3
2
a
AH =
=> H là trung đi m c a c nh BCể ủ ạ
=> AH BC, mà SH BC =>
BC(SAH)
T H h đng vuông góc xu ng SAừ ạ ườ ố
t i Kạ
=> HK là kho ng cách gi a BC và SAả ữ
=>
0
3
AH sin 30 2 4
AH a
HK = = =
V y kho ng cách gi a hai đng th ng BC và SA b ng ậ ả ữ ườ ẳ ằ
3
4
a
0,25 đ
0,25 đ
0,25 đ
0,25 đ
V
Ta có:
3 3 2 6 2
3
2 2
3 3
3
16 64 4
2 3 2 3
a a b a a
b b
+
+ + =
+ +
(1)
3 3 2 6 2
3
2 2
3 3
3
16 64 4
2 3 2 3
b b c c c
c c
+
+ + =
+ +
(2)
3 3 2 6 2
3
2 2
3 3
3
16 64 4
2 3 2 3
c c a c c
a a
+
+ + =
+ +
(3)
L y (1)+(2)+(3) ta đc:ấ ượ
( )
2 2 2
2 2 2
9 3
16 4
abc
P a b c
+ + +
+ + +
(4)
Vì a2+b2+c2=3
T (4)ừ
3
2
P۳
v y giá tr nh nh t ậ ị ỏ ấ
3
2
P=
khi a=b=c=1.
0,5 đ
0,25 đ
0,25 đ
PH N RIÊNG (3 đi m)Ầ ể
A. Theo ch ng trình chu nươ ẩ
VI.a 1 Đng tròn (C) có tâm I(-1;4), bán kính R=5ườ
G i ph ng trình đng th ng c n tìm là ọ ươ ườ ẳ ầ ,
=> : 3x+y+c=0, c≠2 (vì // v i đng th ng 3x+y-2=0)ớ ườ ẳ
Vì đng th ng c t đng tròn theo m t dây cung có đ dài b ng 6=>ườ ẳ ắ ườ ộ ộ ằ
kho ng cách t tâm I đn ả ừ ế b ng ằ
2 2
5 3 4− =
( )
2
4 10 1
3 4
, 4
3 1 4 10 1
c
c
d I
c
= −
− + +
∆ = =� �
+ = − −
(th a mãn c≠2)ỏ
V y ph ng trình đng tròn c n tìm là: ậ ươ ườ ầ
3 4 10 1 0x y+ + − =
ho cặ
0,25 đ
0,25 đ
0,25 đ
4
H
A
C
B
S
K
3 4 10 1 0x y+ − − =
.0,25 đ
2
Ta có
( )
1; 4; 3AB = − − −
uuur
Ph ng trình đng th ng AB: ươ ườ ẳ
1
5 4
4 3
x t
y t
z t
= −
= −
= −
Đ đ dài đo n CD ng n nh t=> D là hình chi u vuông góc c a C trênể ộ ạ ắ ấ ế ủ
c nh AB, g i t a đ đi m D(1-a;5-4a;4-3a)ạ ọ ọ ộ ể
( ;4 3;3 3)DC a a a= − −�uuur
Vì
AB DC⊥
uuur uuur
=>-a-16a+12-9a+9=0<=>
21
26
a=
T a đ đi m ọ ộ ể
5 49 41
; ;
26 26 26
D� �
� �
� �
0,25 đ
0,25 đ
0,25 đ
0,25 đ
VII.a
G i s ph c z=a+biọ ố ứ
Theo bài ra ta có:
( ) ( ) ( )
2 2
2 1 2 2 1 4
32
a b i a b
b a b a
− + + = − + + =
� �
� �
= − = −
2 2
1 2
2 2
1 2
a
b
a
b
= −
= − −
= +
= − +
V y s ph c c n tìm là: z=ậ ố ứ ầ
2 2−
+(
1 2− −
)i; z= z=
2 2+
+(
1 2− +
)i.
0,25 đ
0,25 đ
0,25 đ
0,25 đ
A. Theo ch ng trình nâng caoươ
VI.b
1
Ta có:
( )
100 0 1 2 2 100 100
100 100 100 100
1 ...x C C x C x C x+ = + + + +
(1)
( )
100 0 1 2 2 3 3 100 100
100 100 100 100 100
1 ...x C C x C x C x C x− = − + − + +
(2)
L y (1)+(2) ta đc:ấ ượ
( ) ( )
100 100 0 2 2 4 4 100 100
100 100 100 100
1 1 2 2 2 ... 2x x C C x C x C x+ + − = + + + +
L y đo hàm hai v theo n x ta đcấ ạ ế ẩ ượ
( ) ( )
99 99 2 4 3 100 99
100 100 100
100 1 100 1 4 8 ... 200x x C x C x C x+ − − = + + +
Thay x=1 vào
=>
99 2 4 100
100 100 100
100.2 4 8 ... 200A C C C= = + + +
0,25 đ
0,25 đ
0,25 đ
0,25 đ
2 G i đng th ng c n tìm là d và đng th ng d c t hai đng th ngọ ườ ẳ ầ ườ ẳ ắ ườ ẳ
d1 và d2 l n l t t i đi m A(2+3a;-1+a;-3+2a) và B(3+b;7-2b;1-b).ầ ượ ạ ể
Do đng th ng d đi qua M(3;10;1)=> ườ ẳ
MA k MB=
uuur uuur
( ) ( )
3 1; 11; 4 2 , ; 2 3;MA a a a MB b b b= − − − + = − − −
uuur uuur
3 1 3 1 1
11 2 3 3 2 11 2
4 2 2 4 1
a kb a kb a
a kb k a k kb k
a kb a kb b
− = − = =
� � �
� � �
− = − − + + = =� � �
� � �
� � �
− + = − + = =
� � �
0,25 đ
0,25 đ
0,25 đ
5