Đ THI TH ĐI H CỀ Ử Ạ Ọ NĂM 2014.
Môn thi: TOÁN
Th i gian làm bài:ờ 180 phút
Đ S Ề Ố 7-BB
I.PH N CHUNG CHO T T C CÁC THÍ SINH (7,0 đi m)Ầ Ấ Ả ể
Câu 1 (2,0 đi m)ể
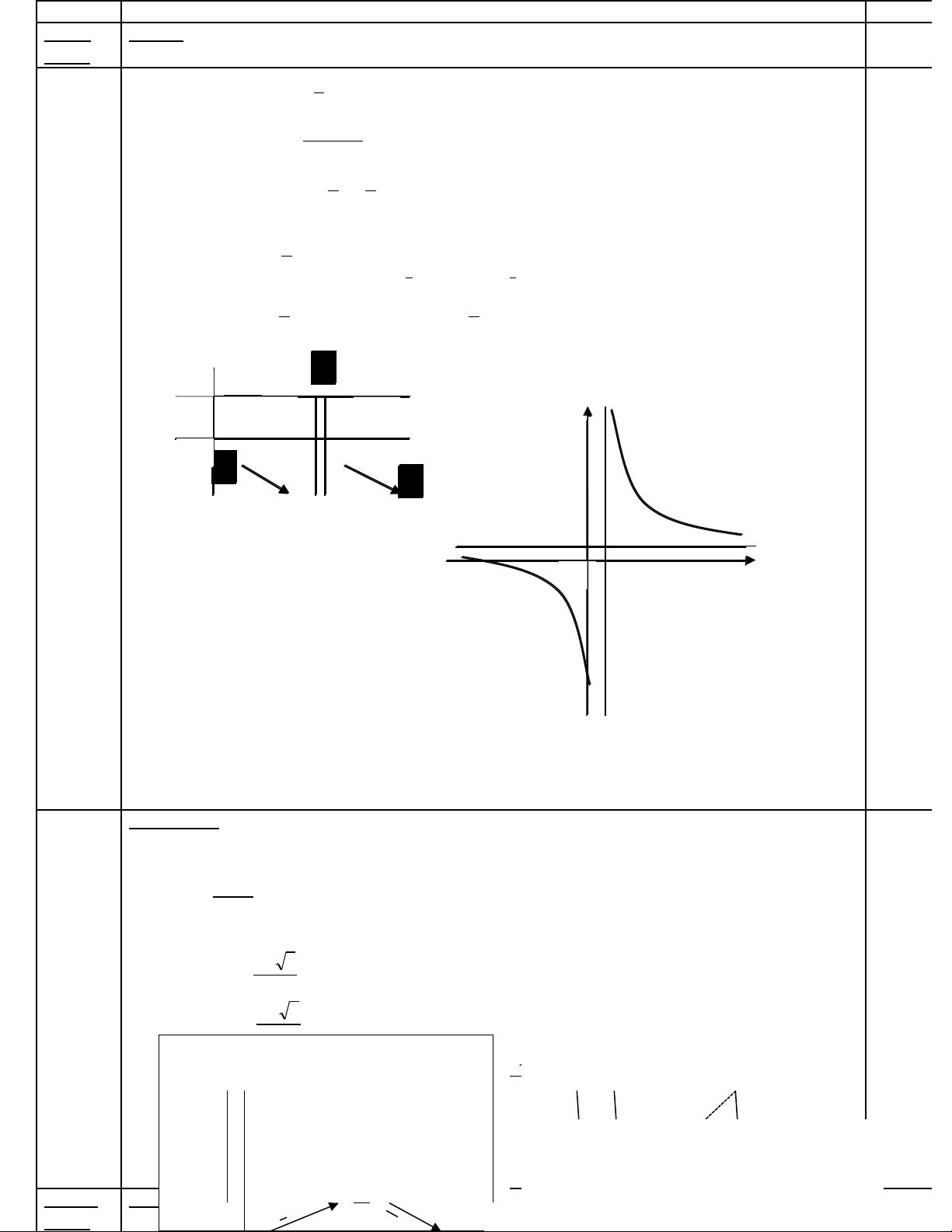
Cho hàm s ố
12
2
x
x
y
1. Kh o sát s bi n thiên và v đ th (C) c a hàm s đã cho.ả ự ế ẽ ồ ị ủ ố
2. Tìm nh ng đi m trên đ th (C) cách đu hai đi m A(2 , 0) và B(0 , 2)ữ ể ồ ị ề ể
Câu 2 (2,0 đi m)ể
1.Gi i ph ng trình : ả ươ
0
10
5cos3
6
3cos5
xx
2.Gi i b t ph ng trình : ả ấ ươ
0
52
232
2
2
xx
xx
Câu III (1,0 đi m)ể
Cho hình ph ng (H) gi i h n b i các đng : ẳ ớ ạ ở ườ
.2;0; xyxyx
Tính th tích kh i tròn xoay t o thành khi cho hình (H) quay quanh tr c Oyể ố ạ ụ
Câu IV (1,0 đi m)ể
Cho lăng tr đngụ ứ tam giác đu ABC.Aề1B1C1 c nh đáy b ng a, c nh bên b ng ạ ằ ạ ằ
2a
.
Tính th tích kh i lăng tr và góc gi a ACể ố ụ ữ 1 và đng cao AH c a ườ ủ tam giác ABC
Câu V (1,0 đi m)ể
Cho :
65
222
cba
. Tìm giá tr l n nh t và nh nh t c a hàm s : ị ớ ấ ỏ ấ ủ ố
)
2
,0(2sin.sin.2
xxcxbay
II. PH N RIÊNG (3,0 đi mẦ ể )Thí sinh ch đc làm m t trong hai ph n (ph n 1 ho c ph n 2ỉ ượ ộ ầ ầ ặ ầ )
1. Theo ch ng trình chu nươ ẩ
Câu VI.a (2,0 đi m)ể
1.Trong m t ph ng v i h t a đ Oxy. Cho đng tròn (C) :ặ ẳ ớ ệ ọ ộ ườ
0124
22 yxyx
và đng th ng d : ườ ẳ
. Tìm nh ng đi m M thu c đng th ng d sao cho t đi m M k đc ữ ể ộ ườ ẳ ừ ể ẻ ượ
đn (C) hai ti p tuy n h p v i nhau góc 90ế ế ế ợ ớ 0
2. Trong không gian v i h t a đ Oxyz. Cho m t c u (S) : ớ ệ ọ ộ ặ ầ
921 2
2
2 zyx
.
L p ph ng trình m t ph ng (P) vuông góc v i đng th ng ậ ươ ặ ẳ ớ ườ ẳ d :
22
1
1
zyx
và c t m t c u (S) theo ắ ặ ầ
đng tròn có bán kính b ng 2 .ườ ằ
CâuVII.a (1,0 đi m)ể
Có bao nhiêu s t nhiên g m b n ch s khác nhau mà m i s đu l n h n 2010.ố ự ồ ố ữ ố ỗ ố ề ớ ơ
2.Theo ch ng trình nâng caoươ
CâuVI.b (2,0 đi m)ể
1.Trong m t ph ng v i h t a đ Oxy. Cho elip (E) : ặ ẳ ớ ệ ọ ộ
044 22 yx
.Tìm nh ng đi m N trên elip (E)ữ ể
sao cho :
( F1 , F2 là hai tiêu đi m c a elip (E) )ể ủ
2.Trong Không gian v i h t a đ Oxyz.Cho đng th ng ớ ệ ọ ộ ườ ẳ
1
2:
z
ty
tx
và đi m ể
)1,0,1( A
Tìm t a đ các đi m E và F thu c đng th ng ọ ộ ể ộ ườ ẳ
đ tam giác AEF là tam giác đu.ể ề
Câu VII.b (1,0 đi m)ể
Tìm s ph c z th a mãn : ố ứ ỏ
4)(
22
22 zz
izziz
----------H t ----------ế
H và tên thí sinh: ………………………………………………; S báo danh: …ọ ố BB01064……..
ĐÁP ÁN THANG ĐI M KH I DỂ Ố
Câu Đáp án Đi mể
I ( 2,0
đi m)ể
1.(1,25)
a/ T p xác đnh : D ậ ị
R
\
2
1
b/ S bi n thiên: ự ế
Dx
x
y
0
)12(
5
2
/
+ H/s ngh ch bi n trên ị ế
),
2
1
(;)
2
1
,(
; H/s không có c c trự ị
+Gi i h n –ti m c n :ớ ạ ệ ậ
yLimyLimyLimyLim
xx
xx
2
1
2
1
;;
2
1
Ti m c n ngang y = ệ ậ
2
1
; Ti m c n đng x = ệ ậ ứ
2
1
c/ Đ th : Đđb x = 0 , y = -2ồ ị
y = 0 , x = -2. Đ th nh n giao đi m 2 ti m c n làm tâm đi x ng.ồ ị ậ ể ệ ậ ố ứ
0,25
0,25
0,25
0,25
0,25
2.(1,0 đi m)ể
Pt đng trung tr c đan AB : y = xườ ự ọ
Nh ng đi m thu c đ th cách đu A và B có hoàng đ là nghi m c a pt :ữ ể ộ ồ ị ề ộ ệ ủ
x
x
x
12
2
2
51
2
51
01
2
x
x
xx
Hai đi m trên đ th th a ycbt : ể ồ ị ỏ
2
51
,
2
51
;
2
51
,
2
51
0,25
0,25
0,25
II ( 2,0
đi m)ể
1.(1,0 đi m)ể
05cos33cos5 xx
2
1
-
2
1
--
Y /
x
2
1
o
y
x
o
2
1
-
2
1
--
Y /
Y
////
/ /
x
2
1
y
x
4
3
+
-
4
13
1
4
3
+
-
4
13
1
1
VII.a(1,0
đi m)ể
VI.a
( 2,0
đi mể)
G i s c n tìm có d ng : ọ ố ầ ạ
abcd
+ N u a > 2 : có 7 cách ch n a và ế ọ
3
9
A
cách ch n b, c , dọ
+ N u a = 2 :ế
+ b > 0 : có 8 cách ch n b và có ọ
2
8
A
cách ch n c , dọ
+ b = 0 và c > 1: có 7 cách ch n c và và 7 cách ch n dọ ọ
+ b = 0 và c = 1 : có 7 cách ch n dọ
V y s các s th a yêu c u bài toán là : ậ ố ố ỏ ầ
403277.7.8.7 2
8
3
9 AA
1.(1,0 đi m)ể
(E) :
33;11;24;1
4
222222
2 cbacbbaay
x
+ Áp d ng đnh lí côsin trong tam giác Fụ ị 1NF2:
18
2
;
9
32
3
4
)(
3
4
.
..2)()(
60cos.2)(
22
22
21
2121
2
21
2
21
0
21
2
2
2
1
2
21
yx
caNFNF
NFNFNFNFNFNFFF
NFNFNFNFFF
V y có 4 đi m th a yêu c u bài toán : ậ ể ỏ ầ
3
1
,
3
24
;
3
1
,
3
24
;
3
1
,
3
24
;
3
1
,
3
24
4321 NNNN
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
2.(1,0 đi m)ể
+ Đng th ng ườ ẳ
)1,0,0(
0
Mquađi
và có vtcp
)0,2,1(
u
;
)2,2,4(,;)2,0,1( 00
uAMAM
+ Kho ng cách t A đn ả ừ ế
là AH =
5
62
,
),(
0
u
uAM
Ad
+ Tam giác AEF đu ề
5
24
3
2
. AHAFAE
.V y E , F thu c m t c u tâm A , BK R = ậ ộ ặ ầ
5
24
và đng th ng ườ ẳ
, nên t a đ E , F là nghi m c a h : ọ ộ ệ ủ ệ
5
32
)1()1(
1
2
222 zyx
z
ty
tx
0,25
0,25
0,25
t =
5
221
suy ra t a đ E và F là : ọ ộ
1
5
242
5
221
1
5
242
5
221
z
y
x
z
y
x
0,25
VII.b
(1,0
đi m)ể
+ G i s ph c z = x + yiọ ố ứ
),( Ryx
0,25
H ệ
44
)22()1(2
xyi
iyiyx
3
3
2
4
1
4
11
4
y
x
x
y
x
y
x
y
V y s ph c c n tìm là : ậ ố ứ ầ
iz 3
3
4
1
4
0,50
0,25
f(t)
f/(