Đ THI TH ĐI H CỀ Ử Ạ Ọ NĂM 2014.
Môn thi: TOÁN
Th i gian làm bài:ờ 180 phút
Đ S 8-BBỀ Ố
PHÂN CHUNG CHO TÂT CA CAC THI SINH (7,0 điêm)
Câu I (2 điêm)
1. Kh o sát s bi n thiên và v đ th (C) c a ham sô ả ự ế ẽ ồ ị ủ
2 1
1
x
yx
−
=−
2. Vi t ph ng trình ti p tuy n c a (C), bi t kho ng cách t đi m I(1;2) đn ti p tuy n b ng ế ươ ế ế ủ ế ả ừ ể ế ế ế ằ
2
.
Câu II (2 điêm)
1) Giai ph ng trình ươ
2
17
sin(2 ) 16 2 3.s in cos 20sin ( )
2 2 12
x
x x x
π π
+ + = + +
2) Giai hê ph ng trình : ươ
4 3 2 2
3 2
1
1
x x y x y
x y x xy
− + =
− + = −
Câu III (1 điêm): Tinh tích phân: I =
4
0
tan .ln(cos )
cos
x x dx
x
π
Câu IV (1 điêm):
Cho hình chóp S.ABC có đáy ABC là tam giác vuông t i A v i AB = a, các m t bên là các tam giác cân t i ạ ớ ặ ạ
đnh S. Hai m t ph ng (SAB) và (SAC) cùng t o v i m t ph ng đáy góc 60ỉ ặ ẳ ạ ớ ặ ẳ 0. Tính côsin c a góc gi a hai m t ủ ữ ặ
ph ng (SAB) và (SBC) .ẳ
Câu V: (1 điêm) Cho a,b,c la cac sô d ng thoa man a + b + c = 1. Ch ng minh r ng: ươ ứ ằ
3
a b b c c a
ab c bc a ca b
+ + +
+ +
+ + +
PHÂN RIÊNG (3 điêm) Thi sinh chi đc lam môt trong hai phân (phân A hoăc B) ươ
A. Theo ch ng trinh Chuânươ
Câu VI.a (1 điêm)
Trong măt phăng toa đô Oxy cho điêm A(1;1) và đng th ng ườ ẳ
: 2x + 3y + 4 = 0.
Tim t a đ đi m B thu c đng th ng ọ ộ ể ộ ườ ẳ
sao cho đng th ng AB và ườ ẳ
h p v i nhau góc 45ợ ớ 0.
Câu VII.a (1 điêm): Trong không gian v i hê toa đô Oxyz, cho điêm M(1;-1;1) ơ
va hai đng th ng ườ ẳ
1
( ) : 1 2 3
x y z
d+
= =
− −
và
Ch ng minh: điêm M, (d), (d’) cung năm trên môt măt phăng. Viêt ph ng trinh măt phăng đo. ư ươ
Câu VIII.a (1 điêm)Gi i ph ng trinh: ả ươ
2 2
2(24 1)
(24 1) (24 1)
log log
x
x x x x
Log x x x
+
+ +
+ =
Theo ch ng trinh Nâng caoươ
Câu VI.b (1 điêm)
Trong măt phăng toa đô Oxy cho đng tron ươ
2 2
( ) : 1C x y+ =
, đng thăng ươ
( ) : 0d x y m+ + =
. Tim
m
đê
( )C
căt
( )d
tai A va B sao cho diên tich tam giac ABO l n nhât. ơ
Câu VII.b (1 điêm)
Trong không gian v i hê toa đô Oxyz, cho ba m t ph ng:ơ ặ ẳ
(P): 2x – y + z + 1 = 0, (Q): x – y + 2z + 3 = 0, (R): x + 2y – 3z + 1 = 0
và đng th ng ườ ẳ
1
:
2
2
x
=
1
1y
=
3
z
. G i ọ
2
là giao tuy n c a (P) và (Q).ế ủ
Vi t ph ng trình đng th ng (d) vuông góc v i (R) và c t c hai đng th ng ế ươ ườ ẳ ớ ắ ả ườ ẳ
1
,
2
.
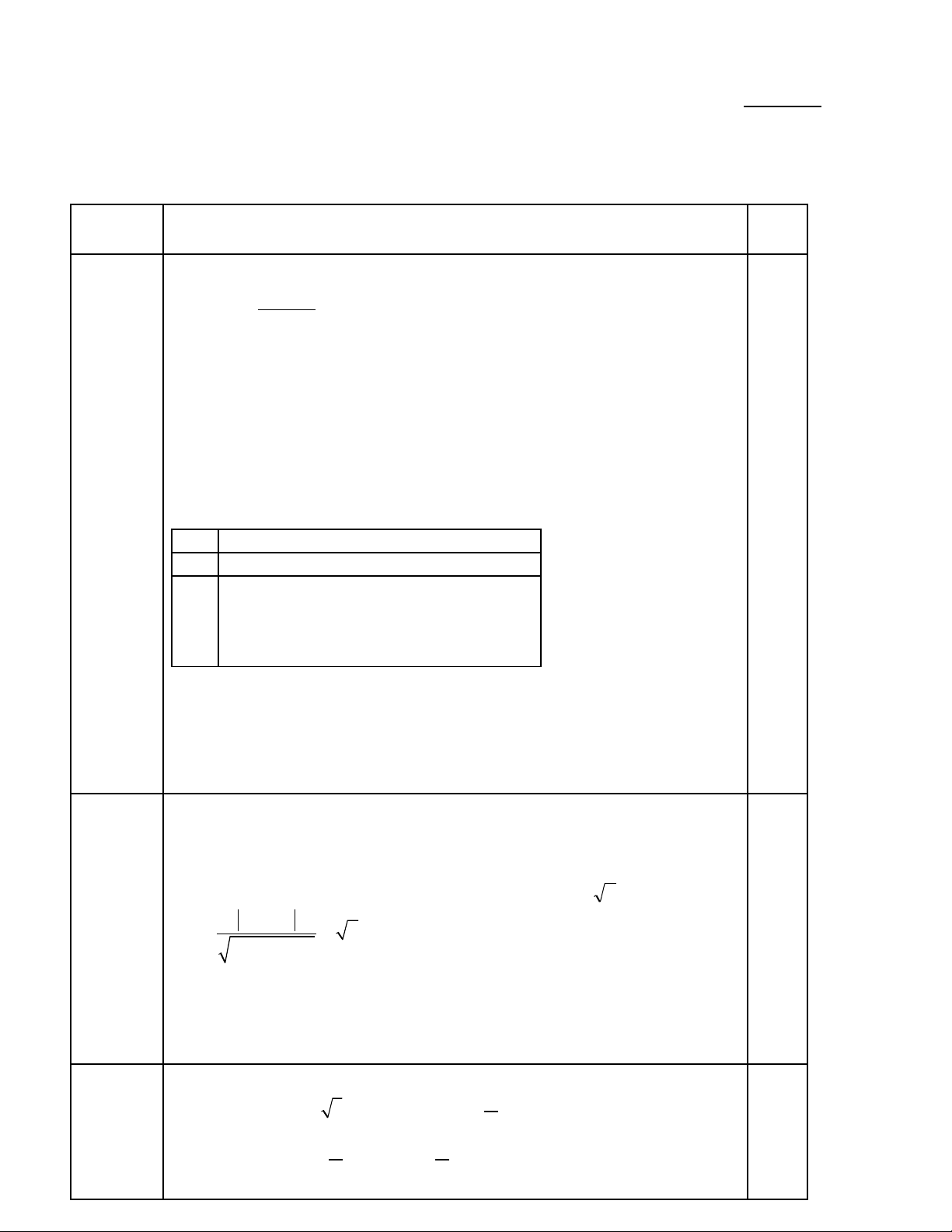
Câu VIII.b (1 điêm) Gi i b t ph ng trình: logả ấ ươ x( log3( 9x – 72 ))
1
----------H t ----------ế
H và tên thí sinh: ………………………………………………; S báo danh: …ọ ố BB01064……..
ĐÁP ÁN VÀ THANG ĐI MỂ
Câu -ýN i dungộĐiể
m
1.1 *T p xác đnh :ậ ị
{ }
\ 1D=ﾡ
*Tính
2
1
' 0
( 1)
y x D
x
−
= < ∀
−
Hàm s ngh ch bi n trên các kho ng ố ị ế ả
( ;1)−
và
(1; )+
*Hàm s không có c c tr ố ự ị
*Gi i h n ớ ạ
1x
Lim y
+
= +
1x
Lim y
−
= −
2
x
Lim y
+
=
2
x
Lim y
−
=
Đ th có ti m c n đng :x=1 , ti m c n ngang y=2 ồ ị ệ ậ ứ ệ ậ
*B ng bi n thiên ả ế
x
−
1
+
y’ - -
y
*V đ th ẽ ồ ị
0.25
0.25
0.25
0.25
1.2 *Ti p tuy n c a (C) t i đi m ế ế ủ ạ ể
0 0
( ; ( )) ( )M x f x C
có ph ng trình ươ
0 0 0
'( )( ) ( )y f x x x f x= − +
Hay
2 2
0 0 0
( 1) 2 2 1 0x x y x x+ − − + − =
(*)
*Kho ng cách t đi m I(1;2) đn ti p tuy n (*) b ng ả ừ ể ế ế ế ằ
2
0
4
0
2 2 2
1 ( 1)
x
x
−=�+ −
gi i đc nghi m ả ượ ệ
0
0x=
và
0
2x=
*Các ti p tuy n c n tìm : ế ế ầ
1 0x y+ − =
và
5 0x y+ − =
0.25
0.25
0.25
0.25
2.1 *Bi n đi ph ng trình đã cho t ng đng v i ế ổ ươ ươ ươ ớ
os2 3 sin 2 10 os( ) 6 0
6
c x x c x
π
− + + + =
os(2 ) 5 os( ) 3 0
3 6
c x c x
π π
+ + + + =�
0.25
0.25
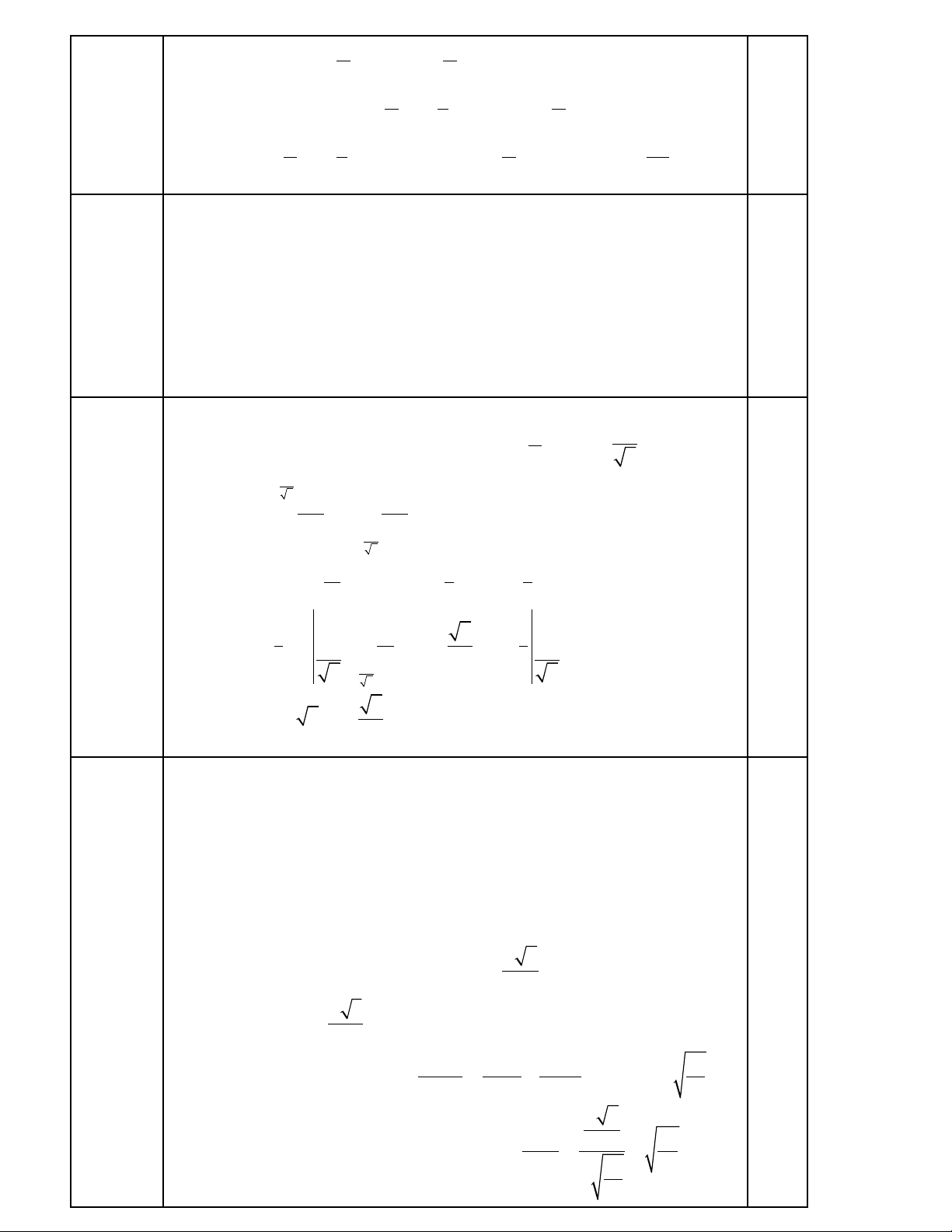
2
2 os ( ) 5 os( ) 2 0
6 6
c x c x
π π
+ + + + =�
Gi i đc ả ượ
1
os( )
6 2
c x
π
+ = −
và
os( ) 2
6
c x
π
+ = −
(lo i)ạ
*Gi i ả
1
os( )
6 2
c x
π
+ = −
đc nghi m ượ ệ
2
2
x k
ππ
= +
và
52
6
x k
ππ
= − +
0.25
0.25
2.2
*Bi n đi h t ng đng v i ế ổ ệ ươ ươ ớ
2 2 3
3 2
( ) 1
( ) 1
x xy x y
x y x xy
− = −
− − = −
*Đt n ph ặ ẩ ụ
2
3
x xy u
x y v
− =
=
, ta đc h ượ ệ
2
1
1
u v
v u
= −
− = −
*Gi i h trên đc nghi m (u;v) là (1;0) và (-2;-3) ả ệ ượ ệ
*T đó gi i đc nghi m (x;y) là (1;0) và (-1;0) ừ ả ượ ệ
0.25
0.25
0.25
0.25
3 *Đt t=cosx ặ
Tính dt=-sinxdx , đi c n x=0 thì t=1 , ổ ậ
4
x
π
=
thì
1
2
t=
T đó ừ
1
1
2
2 2
1
1
2
ln lnt t
I dt dt
t t
= − =
� �
*Đt ặ
2
1
ln ;u t dv dt
t
= =
1 1
;du dt v
t t
= = −�
Suy ra
1
2
1
2
1 1
1 1 2 1
ln ln 2
1 1
2
2 2
I t dt
t t t
= − + = − −
*K t qu ế ả
2
2 1 ln 2
2
I= − −
0.25
0.25
0.25
0.25
4 *V hình ẽ
*G i H là trung đi m BC , ch ng minh ọ ể ứ
( )SH A B C⊥
*Xác đnh đúng góc gi a hai m t ph ng (SAB) , (SAC) v i m t đáy là ị ữ ặ ẳ ớ ặ
0
60SEH SFH= =
*K ẻ
H K S B⊥
, l p lu n suy ra góc gi a hai m t ph ng (SAB) và ậ ậ ữ ặ ẳ
(SBC)
b ng ằ
H K A
.
*L p lu n và tính đc AC=AB=a ,ậ ậ ượ
2
2
a
H A =
,
0
3
tan 60 2
a
SH HF= =
*Tam giác SHK vuông t i H có ạ
2 2 2
1 1 1 3
10
K H a
H K H S H B
= + =�
*Tam giác AHK vuông t i H có ạ
2
20
2
tan 3
3
10
a
A H
A K H K H a
= = =
0.25
0.25
0.25
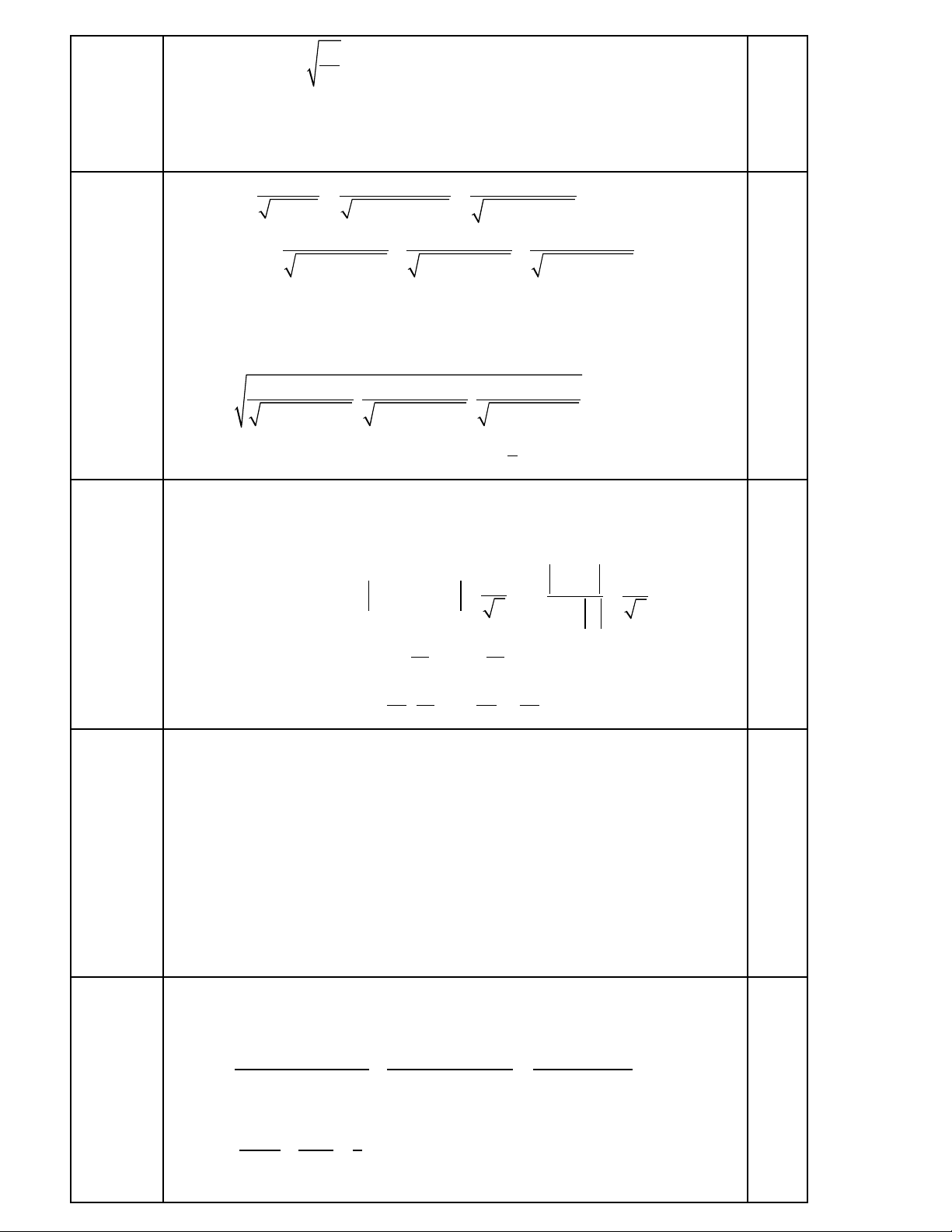
3
cos 23
A K H =�
0.25
5*Bi n đi ế ổ
1 1
1 (1 )(1 )
a b c c
ab c ab b a a b
+ − −
= =
+ + − − − −
*T đó ừ
1 1 1
(1 )(1 ) (1 )(1 ) (1 )(1 )
c b a
V T a b c a c b
− − −
= + +
− − − − − −
Do a,b,c d ng và a+b+c=1 nên a,b,c thu c kho ng (0;1) => 1-a,1-b,1-c ươ ộ ả
d ng ươ
*áp d ng b t đng th c Côsi cho ba s d ng ta đc ụ ấ ẳ ứ ố ươ ượ
3
1 1 1
3. . .
(1 )(1 ) (1 )(1 ) (1 )(1 )
c b a
V T a b c a c b
− − −
− − − − − −
=3 (đpcm)
Đng th c x y ra khi và ch khi ẳ ứ ả ỉ
1
3
a b c===
0.25
0.25
0.25
0.25
6.a *
∆
có ph ng trình tham s ươ ố
1 3
2 2
x t
y t
= −
= − +
và có vtcp
( 3; 2)u= −
ur
*A thu c ộ
∆
(1 3 ; 2 2 )A t t− − +�
*Ta có (AB;
∆
)=450
1
os( ; ) 2
c A B u =�uuuur ur
.1
2
.
A B u
A B u =�
uuuur ur
ur
2
15 3
169 156 45 0 13 13
t t t t− − = = = −� � �
*Các đi m c n tìm là ể ầ
1 2
32 4 22 32
( ; ), ( ; )
13 13 13 13
A A− −
0.25
0.25
0.25
0.25
7.a *(d) đi qua
1
(0; 1;0)M−
và có vtcp
1
(1; 2; 3)u= − −
uur
(d’) đi qua
2
(0;1; 4)M
và có vtcp
2
(1;2;5)u=
uur
*Ta có
1 2
; ( 4; 8; 4)u u O
� �
= − −
� �
uur uur ur
,
1 2
(0;2;4)M M =
uuuuuuur
Xét
1 2 1 2
; . 16 14 0u u M M
� � = − + =
� �
uur uur uuuuuuur
(d) và (d’) đng ph ng .ồ ẳ
*G i (P) là m t ph ng ch a (d) và (d’) => (P) có vtpt ọ ặ ẳ ứ
(1;2; 1)n= −
ur
và đi
qua M1 nên có ph ng trình ươ
2 2 0x y z+ − + =
*D th y đi m M(1;-1;1) thu c mf(P) , t đó ta có đpcm ễ ấ ể ộ ừ
0.25
0.25
0.25
0.25
8.a *Đi u ki n :x>0ề ệ
*TH1 : xét x=1 là nghi m ệ
*TH2 : xét
1x
, bi n đi ph ng trình t ng đng v i ế ổ ươ ươ ươ ớ
1 2 1
1 2log (24 1) 2 log (24 1) log (24 1)
x x x
x x x
+ =
+ + + + +
Đt ặ
log ( 1)
x
x t+ =
, ta đc ph ng trình ượ ươ
1 2 1
1 2 2t t t
+ =
+ +
gi i đc t=1 và t=-2/3 ả ượ
*V i t=1 ớ
log ( 1) 1
x
x+ =�
ph ng trình này vô nghi m ươ ệ
0.25
0.25
0.25
*V i t=-2/3 ớ
2
log ( 1) 3
x
x+ = −�
2 3
.(24 1) 1x x + =�
(*)
Nh n th y ậ ấ
1
8
x=
là nghi m c a (*) ệ ủ
N u ế
1
8
x>
thì VT(*)>1
N u ế
1
8
x<
thì VT(*)<1 , v y (*) có nghi m duy nh t ậ ệ ấ
1
8
x=
*K t lu n : Các nghi m c a ph ng trình đã cho là x=1 và ế ậ ệ ủ ươ
1
8
x=
0.25
6.b *(C) có tâm O(0;0) , bán kính R=1
*(d) c t (C) t i hai đi m phân bi t ắ ạ ể ệ
( ; ) 1d O d <�
*Ta có
1 1 1
. .sin .sin
2 2 2
O A B
S O A O B A O B A O B= =
T đó di n tích tam giác AOB l n nh t khi và ch khi ừ ệ ớ ấ ỉ
0
90A O B =
1
( ; ) 2
d I d =�
1m=� �
0.25
0.25
0.25
0.25
7.b
*
1
∆
có ph ng trình tham s ươ ố
2 2
1
3
x t
y t
z t
= −
= − +
=
*
2
∆
có ph ng trình tham s ươ ố
2
5 3
x s
y s
z s
= +
= +
=
*Gi s ả ử
1 2
;d A d B∆ = ∆ =� �
(2 2 ; 1 ;3 ) B(2+s;5+3s;s)A t t t− − +�
*
( 2 ;3 6; 3 )A B s t s t s t= + − + −
uuuur
, mf(R) có vtpt
(1;2; 3)n= −
ur
*
( ) &d R A B n⊥ uuuur ur
cùng ph ng ươ
2 3 6 3
1 2 3
s t s t s t+ − + −
= =�−
23
24
t=�
*d đi qua
1 1 23
( ; ; )
12 12 8
A
và có vtcp
(1;2; 3)n= −
ur
=> d có ph ng trình ươ
23
1 1
8
12 12
1 2 3
z
x y −
− −
= = −
0.25
0.25
0.25
0.25