http://ebook.here.vn – Download Bài giảng – ðề thi miễn phí
KÌ THI KSCL THI ðẠI HỌC NĂM 2011 LẦN THỨ 1
ðỀ THI MÔN TOÁN -KHỐI A
Thời gian làm bài : 180 phút(không kể thời gian giao ñề)
------------------------------------------
I/PHẦN CHUNG CHO TẤT CẢ THÍ SINH(8,0 ñiểm)
Câu I(2,0 ñiểm): Cho hàm số y = x
4
– 8m
2
x
2
+ 1 (1), với m là tham số thực.
1. Khảo sát sự biến thiên và vẽ ñồ thị của hàm số (1) khi m =
1
2
2. Tìm các giá trị của m ñể hàm số (1) có 3 cực trị A ,B, C và diện tích tam giác ABC
bằng 64.
Câu II(2,0 ñiểm)
1. Giải phương trình :
2
2 3 os2 tan 4sin ( ) cot 2
4
c x x x x
π
− = − +
2.Giải bất phương trình :
2 1 5 3
x x x
− − + > −
Câu III(1,0 ñiểm)
Khai triển (1 – 5x)
30
= a
o
+a
1
x +a
2
x
2
+ .....+ a
30
x
30
Tính tổng S = |a
o
| + 2|a
1
| + 3|a
2
| + ... + 31|a
30
|
Câu IV(2,0 ñiểm): Cho hình chóp S.ABCD , ñáy ABCD là hình vuông cạnh a,mặt bên
SAD là tam giác ñều và SB =
a
. Gọi E,F lần lượt là trung ñiểm của AD và AB .Gọi H
là giao ñiểm của FC và EB.
1.Chứng minh rằng:
SE EB
⊥
và
SBCH
⊥
2.Tính thể tích khối chóp C.SEB
Câu V(1,0 ñiểm).Cho a,b,c là ba số thực dương thoả mãn abc = 1 .Tìm giá trị lớn nhất của
biểu thức :
2 2 2 2 2 2
1 1 1
2 3 2 3 2 3
P
a b b c c a
= + +
+ + + + + +
II/PHẦN RIÊNG (2,0 ñiểm)
Thí sinh chỉ ñược làm một trong hai phần (phần A hoặc phần B)
A/Theo chương trình Chuẩn:
Câu VIa (2,0 ñiểm)
1. Cho tam giác ABC có ñỉnh A (0;1), ñường trung tuyến qua B và ñường phân giác
trong của góc C lần lượt có phương trình : (d1): x – 2y + 4 = 0 và (d2): x + 2y + 2 = 0
Viết phương trình ñường thẳng BC .
2.Giải hệ phương trình :
2log
2
2 3
log log
x
y
y x
x x
x
y
y
= +
=
B/Theo chương trình Nâng cao:
Câu VI b(2,0 ñiểm)
1.Trong mặt phẳng với hệ trục toạ ñộ Oxy,cho hình chữ nhật ABCD có phương trình
ñường thẳng (AB): x – y + 1 = 0 và phương trình ñường thẳng (BD): 2 x + y – 1 = 0;
ñường thẳng (AC) ñi qua M( -1; 1). Tìm toạ ñộ các ñỉnh của hình chữ nhật ABCD.
2.Tìm giá trị lớn nhất ,giá trị nhỏ nhất của hàm số:
2 2
sin 1 os
3 3
x c x
y
+
= +
.
HẾT !
Thí sinh không ñược sử dụng tài liệu.Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:…………………………………………….Số báo danh:……………………
http://ebook.here.vn – Download Bài giảng – ðề thi miễn phí
ðÁP ÁN THANG ðIỂM
ðỀ THI KSCL THI ðẠI HỌC NĂM 2010 LẦN THỨ 1
MÔN TOÁN - KHỐI A
Câu
Ý Nội dung ñáp án ðiểm
I 1
1ñiểm Khi m=
1
2
hàm số ñã cho có pt: y= x
4
– 2x
2
+ 1
1.TXð : D= R
2.SBT
.CBT: y’= 4x
3
- 4x = 4x( x
2
- 1)
------------------------------------------------------------------------------
y’=0 <=> x= 0 hoặc x = 1 hoặc x = -1
Hàm số ñồng biến
( 1;0)
x
∀ ∈ −
vµ
(1; )
+∞
Hàm số nghịch biến
( ; 1)
x
∀ ∈ −∞ −
vµ(0;1)
.Cực trị : HS ñạt cực ñại tại x= 0 và y
Cð
=y(0)=1
HS ñạt cực tiểu tại x=
±
1 và y
CT
=y(
±
1)=0
------------------------------------------------------------------------------
.Giới hạn:
lim
x
y
→+∞
= +∞
;
lim
x
y
→−∞
= +∞
.BBT:
x -
∞
-1 0 1 +
∞
,
y
- 0 + 0 - 0 +
y
+∞
1
+∞
0 0
------------------------------------------------------------------------------
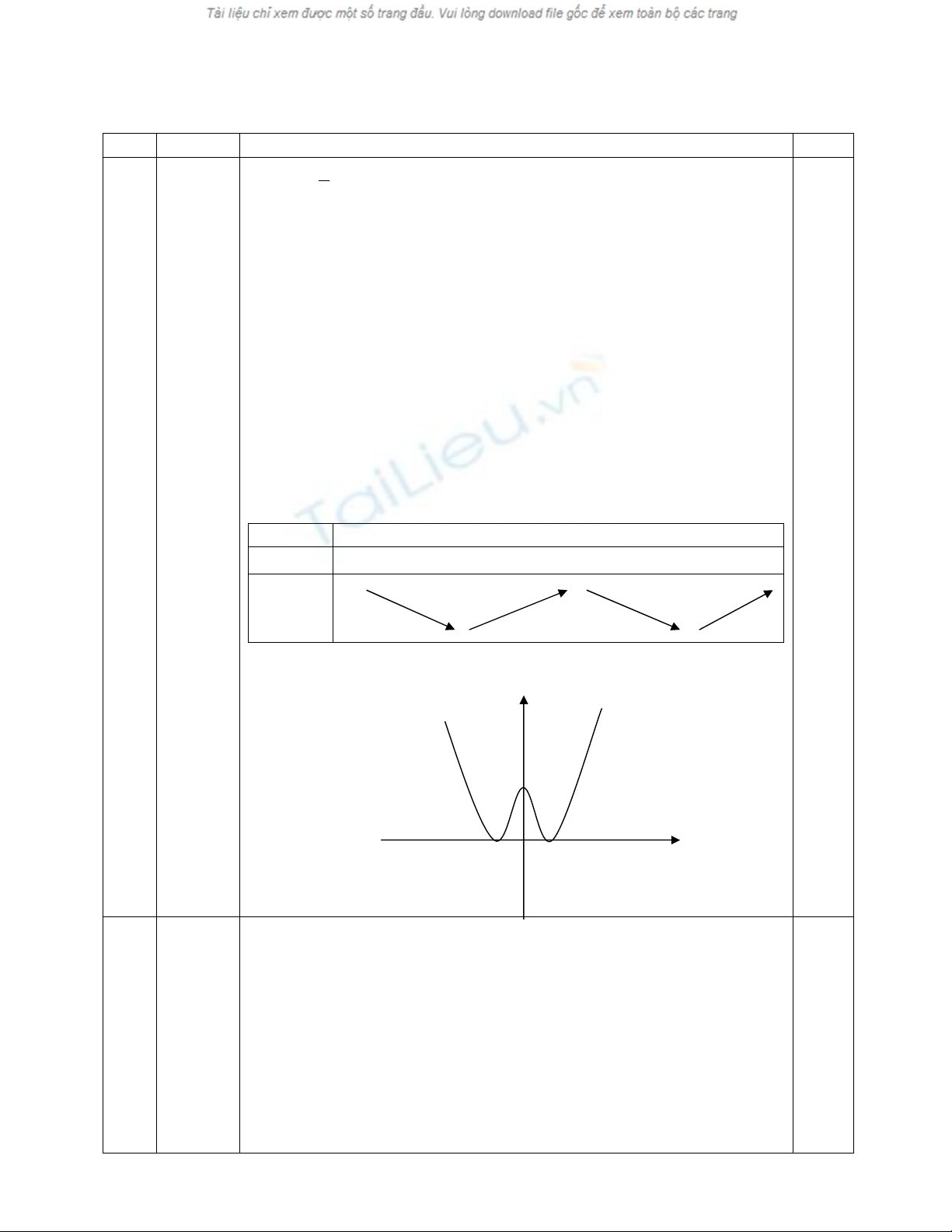
3. vẽ ñồ thị:
y
1
-1 1 x
0,25
0,25
0,25
0,25
I
2
(1ñiểm)
, 3 2 2 2
4 16 4 ( 4 )
y x m x x x m
= − = −
ðk ñể hàm số có 3 cực trị là
,
0
y
=
có 3 nghiệm phân biệt
Tức là phương trình
2 2
( ) 4 0
g x x m
= − =
có hai nghiệm phân biệt
0
x
≠
0
m
⇔ ≠
------------------------------------------------------------------------------
, 4
4
0 1
0 2 1 16
2 1 16
x y
y x m y m
x m y m
= ⇒ =
= ⇔ = ⇒ = −
= − ⇒ = −
0,25
0,25
http://ebook.here.vn – Download Bài giảng – ðề thi miễn phí
Giả sử 3 ñiểm cực trị là:A(0;1);B
4
(2 ;1 16 )
m m
−;C
4
( 2 ;1 16 )
m m
− −
------------------------------------------------------------------------------
Ta thấy AB=AC =
2 4 2
(2 ) (16 )
m m+ nên tam giác ABC cân tại A
Gọi I là trung ñiểm của BC thì
4
(0;1 16 )
I m
−
nên
4
16
AI m
=;
4
BC m
=
------------------------------------------------------------------------------
4
1 1
. . 16 .4
2 2
ABC
S AI BC m m
∆
= =
=64
55
2 2
m m⇔ = ⇔ = ± (tmñk
0
m
≠
)
ðs:
5
2
m= ±
0,25
0,25
II 1
(1ñiểm)
ðk:
( )
2
k
x k Z
π
≠ ∈
------------------------------------------------------------------------------
Với ñk trên phương trình ñã cho tương ñương:
2 3 os2 (t anx cot 2 ) 2 1 os(2 )
2
c x x c x
π
− + = − −
sinx os2
2 3 os2 ( ) 2(1 sin 2 )
cos sin 2
c x
c x x
x x
⇔ − + = −
cos
2 3 os2 2(1 sin 2 )
cos .sin 2
x
c x x
x x
⇔ − = −
1
2 3 os2 2(1 sin 2 )
sin 2
c x x
x
⇔ − = −
------------------------------------------------------------------------------
2
2 3 os2 .sin 2 1 2sin 2 2sin 2
c x x x x
⇔ − = −
3 sin 4 1 2sin 2 1 os4
x x c x
⇔ − = − +
3 sin 4 os4 2sin 2
x c x x
⇔ − =
3 1
sin 4 os4 sin 2
2 2
x c x x
⇔ − =
sin(4 ) sin 2
6
x x
π
⇔ − =
------------------------------------------------------------------------------
⇔
4 2 2 ( )
6 12
( )
7( )4 2 2 36 3
6
x x k x k tm
k Z
k
x tmx x k
ππ
ππ
π π
ππ π
− = + = +
⇔ ∈
= +− = − +
0,25
0,25
0,25
0,25
II 2
(1ñiểm)
2 1 5 3
x x x
− − + > −
(1)
ðk:
1
x
≥
Nhân lượng liên hợp:
2 1 5 0
x x
− + + >
(2 1 5)(2 1 5) ( 3)(2 1 5)
x x x x x x x
− − + − + + > − − + +
4( 1) ( 5) ( 3)(2 1 5)
x x x x x
⇔ − − + > − − + +
3( 3) ( 3)(2 1 5)
x x x x
⇔ − > − − + +
(2)
---------------------------------------------------------------------------
Xét các trường hợp:
TH1:x>3 thì phương trình (2) trở thành:
3 2 1 5
x x
> − + +
(3)
0,25
0,25
http://ebook.here.vn – Download Bài giảng – ðề thi miễn phí
(3)
2 2 2 2 4 2
VP > + =
>3
nên bất phương trình (3) vô nghiệm.
----------------------------------------------------------------------------
TH2: x=3 thì 0>0 (vô lý)
----------------------------------------------------------------------------
TH3:
1 3
x
≤ <
nên từ bất phương trình (2) ta suy ra:
3 (2 1 5)
x x
< − + +
bình phương 2 vế ta ñược:
4 ( 1)( 5) 8 5
x x x
− + > −
(4)
*
8 5 0 8
3
1 3 5
xx
x
− <
⇔ < <
≤ <
(5) thì (4) luôn ñúng
*
8 5 0
8
1
1 3
5
xx
x
− ≥
⇔ ≤ ≤
≤ <
(*) nên bình phương hai vế của (4)ta
ñược
2
9 144 144 0 8 48 8 48
x x x− + < ⇔ − < < +
Kết hợp với ñiều kiện(*) ta ñược:
8
8 48
5
x
− < ≤
(6)
Từ (5) và (6) ta có ñs:
8 48 3
x
− < <
0,25
0,25
III 1ñiểm Xét khai triển:
30 0 1 2 2 30 30
30 30 30 30
(1 5 ) .5 .(5 ) ... .(5 )
x C C x C x C x
− = − + − +
Nhân 2 vế với x ta ñược:
30 0 1 2 2 2 3 30 30 31
30 30 30 30
(1 5 ) .5 .5 ... .5
x x C x C x C x C x
− = − + − +
(1)
------------------------------------------------------------------------------
Lấy ñạo hàm hai vế của (1) ta ñược;
30 29 0 1 2 2 2 30 30 30
30 30 30 30
(1 5 ) 150 (1 5 ) 2 .5 3 .5 ... 31 .5
x x x C C x C x C x
− − − = − + − +
(2)
Chọn x=-1 thay vào (2) ta ñược
30 29 0 1 2 2 30 30
30 30 30 30
6 150.6 2( .5) 3( .5 ) ... 31( .5 )
C C C C+ = + + + +
------------------------------------------------------------------------------
hay
29
0 1 2 30
6 (6 150) 2 3 ... 31
a a a a
+ = + + + +
hay
30
0 1 2 30
6 .26 2 3 ... 31
a a a a
= + + + +
ðS :
30
6 .26
S=
0,25
0,25
0,25
0,25
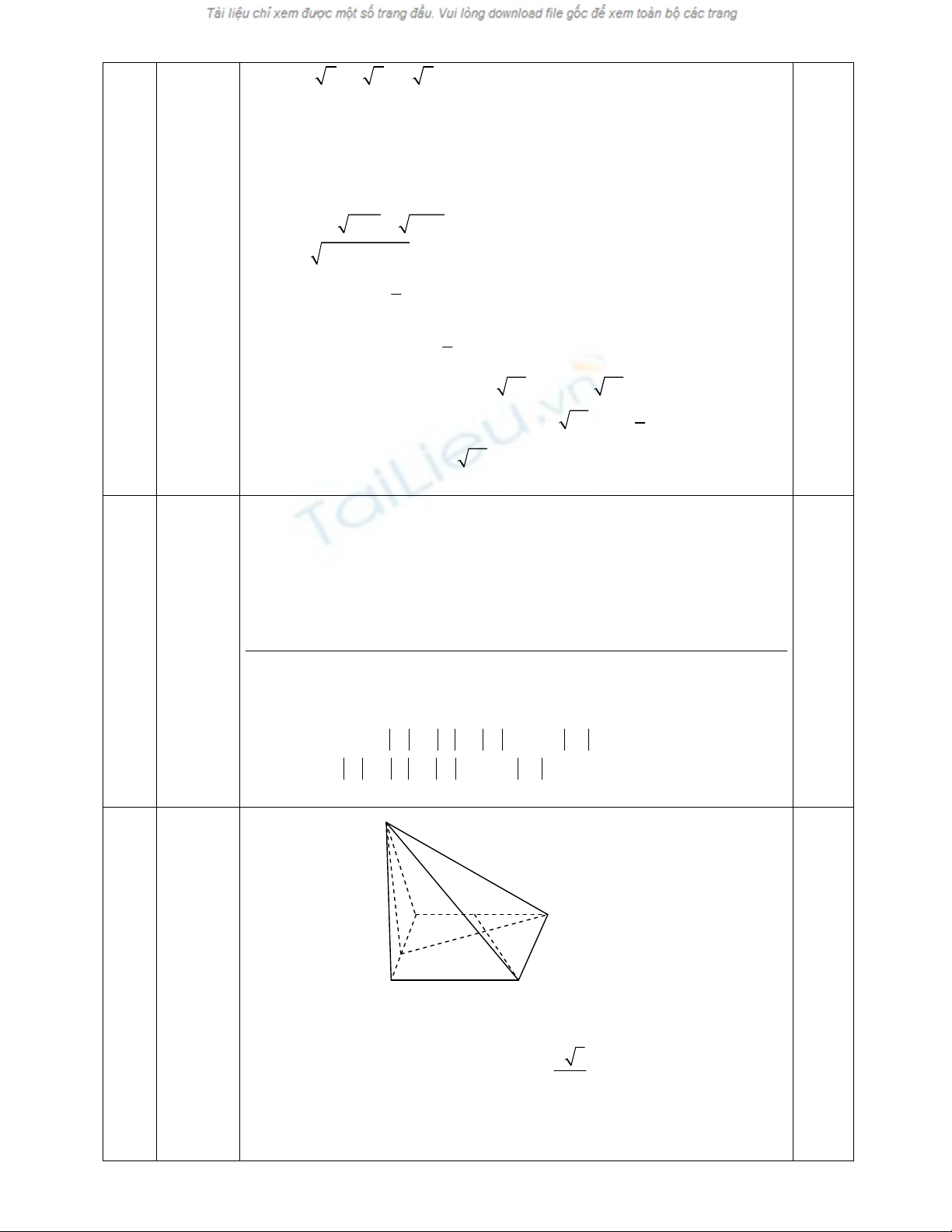
IV 1
(1ñiểm)
S
A F
B
H
E
D C
------------------------------------------------------------------------------
*CM:
SE EB
⊥
Vì tam giác SAD ñều cạnh a
3
2
a
SE⇒ =
Xét tam giác vuông AEB có:
0,25
0,25
http://ebook.here.vn – Download Bài giảng – ðề thi miễn phí
2
2
2 2 2 2
5
2 4
a a
EB EA AB a
= + = + =
-----------------------------------------------------------------------------
Xét tam giác SEB có:
22
2 2 2 2
3 5 2
2 4
a a
SE EB a SB
+ = + = =
suy ra tam giác SEB vuông tại E hay
SE EB
⊥
------------------------------------------------------------------------------
Ta có: AEB = BFC(c-c)
suy ra
¼
¼
AEB BFC
=
mà
¼
¼
0
90
AEB FBE+ =
¼
¼
¼
0 0
90 90
BFC FBE FHB⇒ + = ⇒ =
Hay
CH EB
⊥
mÆt kh¸c
CH SE
⊥
(do
( )
SE ABCD
⊥
)
Suy ra
( )
CH SEB
⊥
. =>
SBCH
⊥
0,25
0,25
IV 2
(1ñiểm)
Vậy
.
1. .
3
C SEB SEB
V CH S
∆
=
------------------------------------------------------------------------------
* Xét FBC có:
2
2 2 2 2 2 2 2
1 1 1 1 1 4 1 5
2
BH BF BC a a a a
a
= + = + = + =
suy ra
2
2
5
a
BH =
------------------------------------------------------------------------------
Xét BHC có:
2 2
2 2 2 2
4 2
5 5
5
a a a
CH BC BH a CH= − = − = ⇒ =
-----------------------------------------------------------------------------
Nên
3
.
1 1 1 2 1 3 5 3
. . . . . . .
3 2 3 2 2 2 12
5
C SEB
a a a a
V CH SE EB= = = (ñvtt)
0,25
0,25
0,25
0,25
V (1
ñiểm)
Áp dụng BðT cosi ta có:
2 2
2
a b ab
+ ≥
2
1 2
b b
+ ≥
suy ra
2 2
2 3 2( 1)
a b ab b
+ + ≥ + +
------------------------------------------------------------------------------
Tương tự :
2 2
2 3 2( 1)
b c bc c
+ + ≥ + +
2 2
2 3 2( 1)
c a ac a
+ + ≥ + +
------------------------------------------------------------------------------
Khi ñó: 1 1 1 1
2 1 1 1
Pab b bc c ac a
≤ + +
+ + + + + +
=
2
1 1
2 1
abc abc
ab b bc c abc ac a bc abc
+ +
+ + + + + +
=
1 1 1
2 1 1 1 2
ab b
ab b ab b ab b
+ + =
+ + + + + +
------------------------------------------------------------------------------
0,25
0,25
0,25